Функция Хевисайда
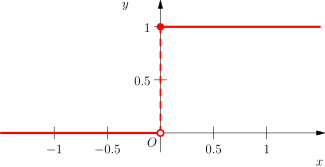
Фу́нкция Хевиса́йда (едини́чная ступе́нчатая функция, функция едини́чного скачка, включённая едини́ца, «ступенька») — кусочно-постоянная функция, равная нулю для отрицательных значений аргумента и единице — для положительных[1]. В нуле эта функция, вообще говоря, не определена, однако её обычно доопределяют в этой точке некоторым числом, чтобы область определения функции содержала все точки действительной оси. Чаще всего неважно, какое значение функция принимает в нуле, поэтому могут использоваться различные определения функции Хевисайда, удобные по тем или иным соображениям, например:
- [math]\displaystyle{ \theta(x)=\begin{cases} 0, & x\lt 0; \\ 1, & x\geqslant 0.\end{cases} }[/math]
Функцию Хевисайда легко записать, используя скобку Айверсона:
- [math]\displaystyle{ \theta(x)=[\,x\geqslant 0\,]. }[/math]
Функция Хевисайда широко используется в математическом аппарате теории управления и теории обработки сигналов для представления сигналов, переходящих в определённый момент времени из одного состояния в другое. В математической статистике эта функция применяется, например, для записи эмпирической функции распределения. Названа в честь Оливера Хевисайда.
Функция Хевисайда является первообразной функцией для дельта-функции Дирака, [math]\displaystyle{ \theta'=\delta }[/math], это также можно записать как (определённый интеграл является числом, для описания первообразной используется неопределённый интеграл [2]):
- [math]\displaystyle{ \theta(x)=\int\limits_{-\infty}^x\!\delta(t)\,dt. }[/math]
Дискретная форма
Можно определить дискретную функцию Хевисайда как функцию от целого аргумента [math]\displaystyle{ n }[/math]:
- [math]\displaystyle{ \theta[n]=\begin{cases}0, & n\lt 0; \\ 1, & n\geqslant 0,\end{cases} }[/math]
где [math]\displaystyle{ n }[/math] — целое число.
Дискретный единичный импульс является первой разностью дискретной функции Хевисайда:
- [math]\displaystyle{ \delta[n]=\theta[n]-\theta[n-1]. }[/math]
Аналитические формы
Для более удобного использования функцию Хевисайда можно аппроксимировать с помощью непрерывной функции:
- [math]\displaystyle{ \theta(x)\approx\frac{1}{2}+\frac{1}{2}\mathrm{th}\,kx=\frac{1}{1+e^{-2kx}}, }[/math]
где большему [math]\displaystyle{ k }[/math] соответствует более крутой подъём функции в точке [math]\displaystyle{ x=0 }[/math]. Задавшись необходимой шириной области перехода функции Хевисайда [math]\displaystyle{ \Delta{x} }[/math], значение [math]\displaystyle{ k }[/math] можно оценить как [math]\displaystyle{ k\approx\frac{10}{\Delta{x}} }[/math].
Если принять [math]\displaystyle{ \theta(0)=1/2 }[/math], уравнение можно записать в предельной форме:
- [math]\displaystyle{ \theta(x)=\lim_{k\to\infty}\frac{1}{2}(1+\mathrm{th}\,kx)=\lim_{k\to\infty}\frac{1}{1+e^{-2kx}}. }[/math]
Существует несколько других аппроксимаций непрерывными функциями:
- [math]\displaystyle{ \theta(x)=\lim_{k\to\infty}\left(\frac{1}{2}+\frac{1}{\pi}\mathrm{arctg}\,kx\right); }[/math]
- [math]\displaystyle{ \theta(x)=\lim_{k\to\infty}\left(\frac{1}{2}+\frac{1}{2}\,\mathrm{erf}\,kx\right). }[/math]
Запись
Часто используется и бывает полезной интегральная форма записи единичной функции:
- [math]\displaystyle{ \theta(x)=-\lim_{\varepsilon\to 0^+}\frac{1}{2\pi i}\int\limits_{-\infty}^\infty\frac{1}{\tau+i\varepsilon}e^{-ix\tau}\,d\tau. }[/math]
Значение в нуле
Значение функции в нуле часто задаётся как [math]\displaystyle{ \theta(0)=0 }[/math], [math]\displaystyle{ \theta(0)=1/2 }[/math] или [math]\displaystyle{ \theta(0)=1 }[/math]. [math]\displaystyle{ \theta(0)=1/2 }[/math] — наиболее употребительный вариант, поскольку по соображениям симметрии в точке разрыва первого рода удобно доопределять функцию средним арифметическим соответствующих односторонних пределов, кроме того в этом случае функция Хевисайда связана с функцией знака:
- [math]\displaystyle{ \theta(x)=\frac{1}{2}(1+\sgn x)=\begin{cases} 0, & x\lt 0; \\ \dfrac{1}{2}, & x=0; \\ 1, & x\gt 0.\end{cases} }[/math]
что с учетом определения функции знака можно выразить как
- [math]\displaystyle{ \theta(x)=\frac{1}{2}\left(1+\frac{|x|}{x}\right)=\frac{x+|x|}{2x} }[/math]
Значение в нуле может явно указываться в записи функции:
- [math]\displaystyle{ \theta_n(x)=\begin{cases}0, & x\lt 0; \\ n, & x=0; \\ 1, & x\gt 0.\end{cases} }[/math]
Преобразование Фурье
Производная функции Хевисайда равна дельта-функции (то есть функция Хевисайда — первообразная дельта-функции):
- [math]\displaystyle{ \theta(x)=\int\limits_{-\infty}^x\delta(t)\,dt }[/math].
Следовательно, применив преобразование Фурье к первообразной дельта-функции [math]\displaystyle{ \theta(t) }[/math], получим её изображение вида:
- [math]\displaystyle{ \frac{1}{2\pi i\omega}+\frac{1}{2}\delta(\omega), }[/math]
то есть:
- [math]\displaystyle{ \theta(t)=\int\limits_{-\infty}^{+\infty}\left(\frac{1}{2\pi i\omega}+\frac{1}{2}\delta(\omega)\right)e^{i\omega t}\,d\omega }[/math]
(второй член — соответствующий нулевой частоте в разложении — описывает постоянное смещение функции Хевисайда вверх; без него получилась бы нечётная функция).
История
Эта функция использовалась ещё до появления её удобного обозначения. Например, Гульельмо Либри[англ.] в 1830-х годах опубликовал несколько работ[3][4], посвящённых функции [math]\displaystyle{ 0^{0^x} }[/math]. По его мнению, [math]\displaystyle{ 0^x }[/math] равен [math]\displaystyle{ 0 }[/math], если [math]\displaystyle{ x\gt 0 }[/math]; [math]\displaystyle{ 1 }[/math], если [math]\displaystyle{ x=0 }[/math] (см. Ноль в нулевой степени); или [math]\displaystyle{ \infin }[/math], если [math]\displaystyle{ x\lt 0 }[/math]. Таким образом Либри заключает, что [math]\displaystyle{ 0^{0^x} }[/math] равняется 1, если [math]\displaystyle{ x\gt 0 }[/math], и 0 в противном случае. Пользуясь нотацией Айверсона, это можно было бы записать, как
- [math]\displaystyle{ 0^{0^x}=[\,x\gt 0\,]. }[/math]
Однако такой нотации в то время не было, и Либри считал достижением, что эту функцию можно выразить через стандартные математические операции. Он использовал эту функцию для выражения абсолютной величины (обозначения [math]\displaystyle{ |x| }[/math] тогда ещё не было, оно было введено позже Вейерштрассом) и индикатора таких условий, как [math]\displaystyle{ a\leq x \leq b }[/math], и даже «[math]\displaystyle{ x }[/math] является делителем [math]\displaystyle{ y }[/math]»[5].
См. также
Примечания
- ↑ В теории автоматического управления и теории операторов Лапласа часто обозначается как [math]\displaystyle{ \scriptstyle{\eta(x)} }[/math]. В англоязычной литературе часто обозначают [math]\displaystyle{ \scriptstyle{H(x)} }[/math] или [math]\displaystyle{ \scriptstyle{1(x)} }[/math]. См., например,
- Волков И. К., Канатников А. Н. Интегральные преобразования и операционное исчисление: Учеб. для вузов / Под ред. B. C. Зарубина, А. П. Крищенко. — 2-е изд. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2002. — 228 с. — (Математика в техническом университете; Вып. XI). — ISBN 5-7038-1273-9.;
- Методы классической и современной теории автоматического управления: Учебник в 5-и тт.; 2-е изд., перераб. и доп. Т. 1: Математические модели, динамические характеристики и анализ систем автоматического управления / Под ред. К. А. Пупкова, Н. Д. Егупова. — М.: Издательство МГТУ им. Н. Э. Баумана, 2004. — 656 с. — ISBN 5-7038-2189-4 (Т. 1).
- ↑ Зорич В.А. Математический анализ. Часть I.. — М.:МЦНМО, 2012. — С. 358.
- ↑ Guillaume Libri. Note sur les valeurs de la fonction 00x, Journal für die reine und angewandte Mathematik 6 (1830), 67-72.
- ↑ Guillaume Libri. Mémoire sur les fonctions discontinues, Journal für die reine und angewandte Mathematik 10 (1833), 303—316.
- ↑ Donald E. Knuth, Two notes on notation, Amer. Math. Monthly 99 no. 5 (May 1992), 403—422 (arXiv: math/9205211 [math.HO] Архивная копия от 20 ноября 2018 на Wayback Machine).