Список квадратурных формул
В данной статье приведен список различных квадратурных формул, для численного интегрирования.
Обозначения
В общем виде формула численного интегрирования записывается следующим образом:
- [math]\displaystyle{ \int\limits_{\Omega_x} f(x) dx = \sum_{i=1}^{m_g} {\widetilde{w_i} f(x_i)} = \sum_{i=1}^{m_g} {w_i \mathrm{det}(J(\xi_i)) f(x(\xi_i))} }[/math],
- [math]\displaystyle{ f(x) }[/math] — интегрируемая функция;
- [math]\displaystyle{ w_i }[/math] — веса интегрирования;
- [math]\displaystyle{ \xi }[/math] — система координат мастер-элемента;
- [math]\displaystyle{ J(\xi) = \frac{\partial(x_1, \dots, x_n)}{\partial(\xi_1, \dots \xi_n)} }[/math] — матрица Якоби для перехода на мастер-элемент.
В силу аддитивности интеграла в качестве области интегрирования [math]\displaystyle{ \Omega }[/math] будут рассматриваться простые области (треугольник, четырёхугольник, тетраэдр и так далее), при сложной геометрии область можно представить как объединение простых и посчитать интеграл по ним или представить с помощью сплайна отображение на мастер-элемент.
В статье для обозначения естественных координат будут использоваться переменные [math]\displaystyle{ x, y, z }[/math], для обозначения координат мастер-элемента — [math]\displaystyle{ \xi, \eta, \zeta }[/math].
Одномерный интеграл

Одномерное интегрирование — это всегда интегрирование по отрезку.
- Область интегрирования: отрезок [math]\displaystyle{ [x_0, x_1] }[/math];
- Мастер-элемент: отрезок [math]\displaystyle{ [-1, 1] }[/math];
- Переход на мастер-элемент: [math]\displaystyle{ \xi(x) = 2 \frac{x-x_0}{x_1 - x_0} - 1 }[/math];
- Переход с мастер-элемента: [math]\displaystyle{ x(\xi) = \frac{(x_1 - x_0)(\xi + 1)}{2} + x_0 }[/math];
- Якобиан: [math]\displaystyle{ \mathrm{det}(J(\xi)) = \frac{x_1 - x_0}{2} }[/math].
| Номер | Число точек | Порядок интегрирования | [math]\displaystyle{ \xi }[/math] | [math]\displaystyle{ w }[/math] | Дополнительно |
|---|---|---|---|---|---|
| 1 | 1 | 1 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 2 }[/math] | Метод прямоугольников |
| 2 | 2 | 1 | [math]\displaystyle{ -1 }[/math] | [math]\displaystyle{ 1 }[/math] | Метод трапеций |
| [math]\displaystyle{ 1 }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| 3 | 2 | 3 | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | Метод Гаусса-2 |
| [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| 4 | 3 | 3 | [math]\displaystyle{ -1 }[/math] | [math]\displaystyle{ \frac{1}{3} }[/math] | Метод Симпсона |
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{4}{3} }[/math] | ||||
| [math]\displaystyle{ 1 }[/math] | [math]\displaystyle{ \frac{1}{3} }[/math] | ||||
| 5 | 3 | 5 | [math]\displaystyle{ -\sqrt{\frac{3}{5}} }[/math] | [math]\displaystyle{ \frac{5}{9} }[/math] | Метод Гаусса-3 |
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{8}{9} }[/math] | ||||
| [math]\displaystyle{ \sqrt{\frac{3}{5}} }[/math] | [math]\displaystyle{ \frac{5}{9} }[/math] | ||||
| 6 | 4 | 7 | [math]\displaystyle{ -\sqrt{\frac{3}{7} - \frac{2}{7} \sqrt{\frac{6}{5}}} }[/math] | [math]\displaystyle{ \frac{18+\sqrt{30}}{36} }[/math] | Метод Гаусса-4 |
| [math]\displaystyle{ \sqrt{\frac{3}{7} - \frac{2}{7} \sqrt{\frac{6}{5}}} }[/math] | [math]\displaystyle{ \frac{18+\sqrt{30}}{36} }[/math] | ||||
| [math]\displaystyle{ -\sqrt{\frac{3}{7} + \frac{2}{7} \sqrt{\frac{6}{5}}} }[/math] | [math]\displaystyle{ \frac{18-\sqrt{30}}{36} }[/math] | ||||
| [math]\displaystyle{ \sqrt{\frac{3}{7} + \frac{2}{7} \sqrt{\frac{6}{5}}} }[/math] | [math]\displaystyle{ \frac{18-\sqrt{30}}{36} }[/math] | ||||
| 7 | 5 | 9 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{128}{225} }[/math] | Метод Гаусса-5 |
| [math]\displaystyle{ -\frac{1}{3}\sqrt{5 - 2\sqrt{\frac{10}{7}}} }[/math] | [math]\displaystyle{ \frac{322+13\sqrt{70}}{900} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{3}\sqrt{5 - 2\sqrt{\frac{10}{7}}} }[/math] | [math]\displaystyle{ \frac{322+13\sqrt{70}}{900} }[/math] | ||||
| [math]\displaystyle{ -\frac{1}{3}\sqrt{5 + 2\sqrt{\frac{10}{7}}} }[/math] | [math]\displaystyle{ \frac{322-13\sqrt{70}}{900} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{3}\sqrt{5 + 2\sqrt{\frac{10}{7}}} }[/math] | [math]\displaystyle{ \frac{322-13\sqrt{70}}{900} }[/math] |
Двухмерный интеграл
Квадратный мастер-элемент
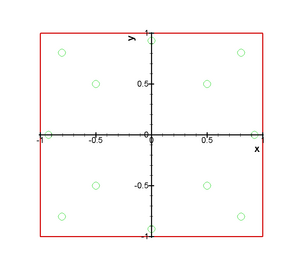
- Область интегрирования: прямоугольник [math]\displaystyle{ [x_0, x_1] \times [y_0, y_1] }[/math]
- Мастер-элемент: квадрат [math]\displaystyle{ [-1, 1] \times [-1, 1] }[/math]
- Переход на мастер-элемент:
- [math]\displaystyle{ \xi(x, y) = 2 \frac{x-x_0}{x_1 - x_0} - 1 }[/math]
- [math]\displaystyle{ \eta(x, y) = 2 \frac{y-y_0}{y_1 - y_0} - 1 }[/math];
- Переход с мастер-элемента:
- [math]\displaystyle{ x(\xi, \eta) = \frac{(x_1 - x_0)(\xi + 1)}{2} + x_0 }[/math]
- [math]\displaystyle{ y(\xi, \eta) = \frac{(y_1 - y_0)(\eta + 1)}{2} + y_0 }[/math];
- Якобиан: [math]\displaystyle{ \mathrm{det}(J(\xi, \eta)) = \frac{(x_1 - x_0)(y_1 - y_0)}{4} }[/math].
Данные формулы интегрирования можно использовать и когда область интегрирования — выпуклый четырёхугольник, но тогда формулы перехода на мастер-элемент (и обратно) не будут иметь такой простой вид. Получить выражение для перехода можно используя интерполяционный полином.
Многие из формул интегрирования по квадрату можно получить, как комбинацию формул по отрезку: в качестве точек интегрирования берутся все возможные пары одномерных точек, а в качестве весов — соответствующие произведения весов интегрирования. Примерами таких методов в таблице ниже являются метод прямоугольников, метод трапеций и метод Гаусса-2.
| Номер | Число точек | Порядок интегрирования | [math]\displaystyle{ \xi }[/math] | [math]\displaystyle{ \eta }[/math] | [math]\displaystyle{ w }[/math] | Дополнительно |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 4 }[/math] | Метод прямоугольников (метод среднего) |
| 2 | 4 | 1 | [math]\displaystyle{ -1 }[/math] | [math]\displaystyle{ -1 }[/math] | [math]\displaystyle{ 1 }[/math] | Метод трапеций |
| [math]\displaystyle{ -1 }[/math] | [math]\displaystyle{ 1 }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ 1 }[/math] | [math]\displaystyle{ -1 }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ 1 }[/math] | [math]\displaystyle{ 1 }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| 3 | 4 | 3 | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | Метод Гаусса-2 |
| [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| 4 | 12 | 7 | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_c }[/math] | [math]\displaystyle{ a = \sqrt{\frac{114-3\sqrt{583}}{287}} }[/math] [math]\displaystyle{ b = \sqrt{\frac{114+3\sqrt{583}}{287}} }[/math] [math]\displaystyle{ c = \sqrt{\frac{6}{7}} }[/math] [math]\displaystyle{ w_a = \frac{307}{810} + \frac{923}{270\sqrt{583}} }[/math] [math]\displaystyle{ w_b = \frac{307}{810} - \frac{923}{270\sqrt{583}} }[/math] [math]\displaystyle{ w_c = \frac{98}{405} }[/math] Число узлов минимально[1]. |
| [math]\displaystyle{ c }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_c }[/math] | ||||
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ w_c }[/math] | ||||
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ w_c }[/math] | ||||
| [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ w_a }[/math] | ||||
| [math]\displaystyle{ a }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ w_a }[/math] | ||||
| [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ w_a }[/math] | ||||
| [math]\displaystyle{ a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ w_a }[/math] | ||||
| [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ w_b }[/math] | ||||
| [math]\displaystyle{ b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ w_b }[/math] | ||||
| [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ w_b }[/math] | ||||
| [math]\displaystyle{ b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ w_b }[/math] |
Треугольный мастер-элемент
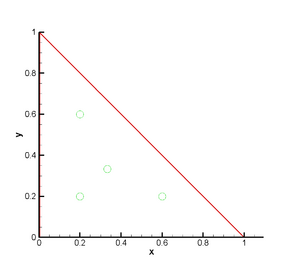
- Область интегрирования: треугольник, образованный вершинами [math]\displaystyle{ (x_1, y_1), (x_2, y_2), (x_3, y_3) }[/math];
- Мастер-элемент: треугольник, образованный вершинами [math]\displaystyle{ (0,0), (1, 0), (0, 1) }[/math].
Для перехода на мастер-элемент используются барицентрические координаты (L-координаты), обозначим их [math]\displaystyle{ \lambda_1, \lambda_2, \lambda_3 }[/math].
- [math]\displaystyle{ \lambda_i(x,y) = \alpha_{i1} x + \alpha_{i2} y + \alpha_{i3} }[/math]
Для вычисления коэффициентов L-координат используется матрица [math]\displaystyle{ D }[/math]:
- [math]\displaystyle{ D = \begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ 1 & 1 & 1 \end{pmatrix} }[/math]
Матрица коэффициентов обратна к [math]\displaystyle{ D }[/math]: [math]\displaystyle{ \Alpha = D^{-1} }[/math].
- Переход на мастер элемент:
- [math]\displaystyle{ \xi(x,y) = \lambda_1(x,y) }[/math]
- [math]\displaystyle{ \eta(x,y) = \lambda_2(x,y) }[/math]
- Переход с мастер элемента:
- [math]\displaystyle{ \begin{pmatrix} x \\ y \\ 1\end{pmatrix} = D \begin{pmatrix} \xi \\ \eta \\ 1 - \xi - \eta \end{pmatrix} }[/math]
- Якобиан : [math]\displaystyle{ \mathrm{det}(J(\xi,\eta)) = \mathrm{det}(D) }[/math].
| Номер | Число точек | Порядок интегрирования | [math]\displaystyle{ \xi }[/math] | [math]\displaystyle{ \eta }[/math] | [math]\displaystyle{ w }[/math] | Дополнительно |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | [math]\displaystyle{ \frac{1}{3} }[/math] | [math]\displaystyle{ \frac{1}{3} }[/math] | [math]\displaystyle{ \frac{1}{2} }[/math] | Метод среднего |
| 2 | 3 | 2 | [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | - |
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | ||||
| 2 | 3 | 2 | [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | Метод Гаусса-3 |
| [math]\displaystyle{ \frac{2}{3} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{2}{3} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | ||||
| 4 | 4 | 3 | [math]\displaystyle{ \frac{1}{3} }[/math] | [math]\displaystyle{ \frac{1}{3} }[/math] | [math]\displaystyle{ -\frac{9}{32} }[/math] | Метод Гаусса-4 |
| [math]\displaystyle{ \frac{3}{5} }[/math] | [math]\displaystyle{ \frac{1}{5} }[/math] | [math]\displaystyle{ \frac{25}{96} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{5} }[/math] | [math]\displaystyle{ \frac{3}{5} }[/math] | [math]\displaystyle{ \frac{25}{96} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{5} }[/math] | [math]\displaystyle{ \frac{1}{5} }[/math] | [math]\displaystyle{ \frac{25}{96} }[/math] | ||||
| 5 | 7 | 3 | [math]\displaystyle{ \frac{1}{3} }[/math] | [math]\displaystyle{ \frac{1}{3} }[/math] | [math]\displaystyle{ \frac{9}{40} }[/math] | Метод Ньютона-Котеса (англ. Newton-Cotes (англ.)) |
| [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{1}{15} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ \frac{1}{15} }[/math] | ||||
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ \frac{1}{15} }[/math] | ||||
| [math]\displaystyle{ 1 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{1}{40} }[/math] | ||||
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 1 }[/math] | [math]\displaystyle{ \frac{1}{40} }[/math] | ||||
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{1}{40} }[/math] |
Трёхмерный интеграл
Кубический мастер-элемент

- Область интегрирования: параллелепипед [math]\displaystyle{ [x_0, x_1] \times [y_0, y_1] \times [z_0, z_1] }[/math]
- Мастер-элемент: куб [math]\displaystyle{ [-1, 1] \times [-1, 1] \times [-1, 1] }[/math]
- Переход на мастер-элемент:
- [math]\displaystyle{ \xi(x, y, z) = 2 \frac{x-x_0}{x_1 - x_0} - 1 }[/math]
- [math]\displaystyle{ \eta(x, y, z) = 2 \frac{y-y_0}{y_1 - y_0} - 1 }[/math]
- [math]\displaystyle{ \zeta(x, y, z) = 2 \frac{z-z_0}{z_1 - z_0} - 1 }[/math]
- Переход с мастер-элемента:
- [math]\displaystyle{ x(\xi, \eta, \zeta) = \frac{(x_1 - x_0)(\xi + 1)}{2} + x_0 }[/math]
- [math]\displaystyle{ y(\xi, \eta, \zeta) = \frac{(y_1 - y_0)(\eta + 1)}{2} + y_0 }[/math];
- [math]\displaystyle{ z(\xi, \eta, \zeta) = \frac{(z_1 - z_0)(\zeta + 1)}{2} + z_0 }[/math];
- Якобиан: [math]\displaystyle{ \mathrm{det}(J(\xi, \eta, \zeta)) = \frac{(x_1 - x_0)(y_1 - y_0)(z_1 - z_0)}{8} }[/math].
Аналогично как и для квадрата, куб можно использовать как мастер-элемент для произвольного шестигранника[уточнить], но тогда формулы перехода и якобиана усложнится.
Так же, аналогично с квадратом, многие формулы интегрирования по кубу можно получить из формул интегрирования по отрезку, координаты узлов — это все возможные тройки координат одномерной формулы, а веса интегрирования — произведение соответствующих весов одномерной формулы.
| Номер | Число точек | Порядок интегрирования | [math]\displaystyle{ \xi }[/math] | [math]\displaystyle{ \eta }[/math] | [math]\displaystyle{ \zeta }[/math] | [math]\displaystyle{ w }[/math] | Дополнительно |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 8 }[/math] | Метод прямоугольников (метод среднего) |
| 2 | 8 | 3 | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | Метод Гаусса-2 |
| [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ -\frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ \frac{1}{\sqrt{3}} }[/math] | [math]\displaystyle{ 1 }[/math] | ||||
| 3 | 14 | 5 | [math]\displaystyle{ -\sqrt{\frac{19}{30}} }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{320}{361} }[/math] | Число узлов в классе формул с порядком аппроксимации 5 и не содержащих начало координат минимально.[2] |
| [math]\displaystyle{ \sqrt{\frac{19}{30}} }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{320}{361} }[/math] | ||||
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{30}} }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{320}{361} }[/math] | ||||
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{30}} }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \frac{320}{361} }[/math] | ||||
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{30}} }[/math] | [math]\displaystyle{ \frac{320}{361} }[/math] | ||||
| [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{30}} }[/math] | [math]\displaystyle{ \frac{320}{361} }[/math] | ||||
| [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \frac{121}{361} }[/math] | ||||
| [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \frac{121}{361} }[/math] | ||||
| [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \frac{121}{361} }[/math] | ||||
| [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \frac{121}{361} }[/math] | ||||
| [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \frac{121}{361} }[/math] | ||||
| [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \frac{121}{361} }[/math] | ||||
| [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ -\sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \frac{121}{361} }[/math] | ||||
| [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \sqrt{\frac{19}{33}} }[/math] | [math]\displaystyle{ \frac{121}{361} }[/math] |
Поскольку формулы интегрирования высоких порядков содержат много точек, то их приведём отдельно.
- Порядок: 7, число точек: 34
| Номер точки | [math]\displaystyle{ \xi }[/math] | [math]\displaystyle{ \eta }[/math] | [math]\displaystyle{ \zeta }[/math] | [math]\displaystyle{ w }[/math] | Дополнительно |
|---|---|---|---|---|---|
| 1 | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_1 }[/math] | [math]\displaystyle{ a = \sqrt{\frac{6}{7}} }[/math], [math]\displaystyle{ b = \sqrt{\frac{960 - 33\sqrt{238}}{2726}} }[/math], [math]\displaystyle{ c = \sqrt{\frac{960 + 33\sqrt{238}}{2726}} }[/math], [math]\displaystyle{ w_1 = \frac{1078}{3645} }[/math], [math]\displaystyle{ w_2 = \frac{343}{3645} }[/math], [math]\displaystyle{ w_3 = \frac{43}{135} + \frac{829\sqrt{238}}{136323} }[/math], [math]\displaystyle{ w_4= \frac{43}{135} - \frac{829\sqrt{238}}{136323} }[/math] |
| 2 | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_1 }[/math] | |
| 3 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_1 }[/math] | |
| 4 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_1 }[/math] | |
| 5 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ w_1 }[/math] | |
| 6 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ w_1 }[/math] | |
| 7 | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 8 | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 9 | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 10 | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 11 | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 12 | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 13 | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 14 | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 15 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 16 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 17 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 18 | [math]\displaystyle{ 0 }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ -a }[/math] | [math]\displaystyle{ w_2 }[/math] | |
| 19 | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ w_3 }[/math] | |
| 20 | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ w_3 }[/math] | |
| 21 | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ w_3 }[/math] | |
| 22 | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ w_3 }[/math] | |
| 23 | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ w_3 }[/math] | |
| 24 | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ w_3 }[/math] | |
| 25 | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ w_3 }[/math] | |
| 26 | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ -b }[/math] | [math]\displaystyle{ w_3 }[/math] | |
| 27 | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ w_4 }[/math] | |
| 28 | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ w_4 }[/math] | |
| 29 | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ w_4 }[/math] | |
| 30 | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ w_4 }[/math] | |
| 31 | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ w_4 }[/math] | |
| 32 | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ w_4 }[/math] | |
| 33 | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ w_4 }[/math] | |
| 34 | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ -c }[/math] | [math]\displaystyle{ w_4 }[/math] |
Тетраэдральный мастер-элемент
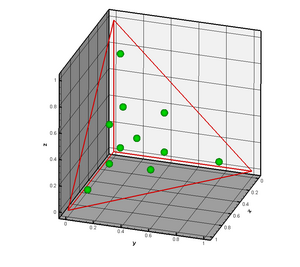
- Область интегрирования: тетраэдр, образованный вершинами [math]\displaystyle{ (x_1, y_1, z_1), (x_2, y_2, z_2), (x_3, y_3, y_3), (x_4, y_4, z_4) }[/math].
- Мастер-элемент: тетраэдр, образованный вершинами [math]\displaystyle{ (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1) }[/math].
Аналогично с треугольником для перехода на мастер-элемент используются L-координаты тетраэдра, обозначим их [math]\displaystyle{ \lambda_1, \lambda_2, \lambda_3, \lambda_4 }[/math]:
- [math]\displaystyle{ \lambda_i(x,y,z) = \alpha_{i1} x + \alpha_{i2} y + \alpha_{i3} z + \alpha_{i4} }[/math]
Матрица коэффициентов определяется, как: [math]\displaystyle{ \Alpha = D^{-1} }[/math], где
- [math]\displaystyle{ D = \begin{pmatrix} x_1 & x_2 & x_3 & x_4 \\ y_1 & y_2 & y_3 & y_4 \\ z_1 & z_2 & z_3 & z_4 \\ 1 & 1 & 1 & 1 \end{pmatrix} }[/math]
- Переход на мастер-элемент:
- [math]\displaystyle{ \xi(x,y,z) = \lambda_1(x,y,z) }[/math]
- [math]\displaystyle{ \eta(x,y,z) = \lambda_2(x,y,z) }[/math]
- [math]\displaystyle{ \zeta(x,y,z) = \lambda_3(x,y,z) }[/math]
- Переход с мастер-элемента:
- [math]\displaystyle{ \begin{pmatrix} x \\ y \\ z \\ 1\end{pmatrix} = D \begin{pmatrix} \xi \\ \eta \\ \zeta \\ 1 - \xi - \eta - \zeta\end{pmatrix} }[/math]
- Якобиан : [math]\displaystyle{ \mathrm{det}(J(\xi,\eta, \zeta)) = \mathrm{det}(D) }[/math].
| Номер | Число точек | Порядок интегрирования | [math]\displaystyle{ \xi }[/math] | [math]\displaystyle{ \eta }[/math] | [math]\displaystyle{ \zeta }[/math] | [math]\displaystyle{ w }[/math] | Дополнительно |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | [math]\displaystyle{ \frac{1}{4} }[/math] | [math]\displaystyle{ \frac{1}{4} }[/math] | [math]\displaystyle{ \frac{1}{4} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | Метод среднего |
| 2 | 4 | 2 | [math]\displaystyle{ \frac{5+3\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{5-\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{5-\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{1}{24} }[/math] | Метод Гаусса-4 |
| [math]\displaystyle{ \frac{5-\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{5+3\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{5-\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{1}{24} }[/math] | ||||
| [math]\displaystyle{ \frac{5-\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{5-\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{5+3\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{1}{24} }[/math] | ||||
| [math]\displaystyle{ \frac{5-\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{5-\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{5-\sqrt{5}}{20} }[/math] | [math]\displaystyle{ \frac{1}{24} }[/math] | ||||
| 3 | 5 | 3 | [math]\displaystyle{ \frac{1}{4} }[/math] | [math]\displaystyle{ \frac{1}{4} }[/math] | [math]\displaystyle{ \frac{1}{4} }[/math] | [math]\displaystyle{ -\frac{2}{15} }[/math] | |
| [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{3}{40} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{3}{40} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{1}{2} }[/math] | [math]\displaystyle{ \frac{3}{40} }[/math] | ||||
| [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{1}{6} }[/math] | [math]\displaystyle{ \frac{3}{40} }[/math] | ||||
| 4 | 11 | 4 | [math]\displaystyle{ \frac{1}{4} }[/math] | [math]\displaystyle{ \frac{1}{4} }[/math] | [math]\displaystyle{ \frac{1}{4} }[/math] | [math]\displaystyle{ -\frac{74}{5625} }[/math] | Метод Гаусса-11 |
| [math]\displaystyle{ \frac{11}{14} }[/math] | [math]\displaystyle{ \frac{5}{70} }[/math] | [math]\displaystyle{ \frac{5}{70} }[/math] | [math]\displaystyle{ \frac{343}{45000} }[/math] | ||||
| [math]\displaystyle{ \frac{5}{70} }[/math] | [math]\displaystyle{ \frac{11}{14} }[/math] | [math]\displaystyle{ \frac{5}{70} }[/math] | [math]\displaystyle{ \frac{343}{45000} }[/math] | ||||
| [math]\displaystyle{ \frac{5}{70} }[/math] | [math]\displaystyle{ \frac{5}{70} }[/math] | [math]\displaystyle{ \frac{11}{14} }[/math] | [math]\displaystyle{ \frac{343}{45000} }[/math] | ||||
| [math]\displaystyle{ \frac{5}{70} }[/math] | [math]\displaystyle{ \frac{5}{70} }[/math] | [math]\displaystyle{ \frac{5}{70} }[/math] | [math]\displaystyle{ \frac{343}{45000} }[/math] | ||||
| [math]\displaystyle{ \frac{1+\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1-\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1-\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{56}{2250} }[/math] | ||||
| [math]\displaystyle{ \frac{1-\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1+\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1-\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{56}{2250} }[/math] | ||||
| [math]\displaystyle{ \frac{1-\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1-\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1+\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{56}{2250} }[/math] | ||||
| [math]\displaystyle{ \frac{1-\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1+\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1+\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{56}{2250} }[/math] | ||||
| [math]\displaystyle{ \frac{1+\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1-\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1+\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{56}{2250} }[/math] | ||||
| [math]\displaystyle{ \frac{1+\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1+\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{1-\sqrt{5/14}}{4} }[/math] | [math]\displaystyle{ \frac{56}{2250} }[/math] | ||||
| 5 | 14 | 5 | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ A }[/math] | [math]\displaystyle{ A,\ B, \ C,\ a,\ b,\ c }[/math] определяются из следующих уравнений:
[math]\displaystyle{ \begin{cases} t = \frac{4}{27}\left(71 - 4\sqrt{79}\sin\left(\frac{1}{3}\left[\frac{\pi}{2} + \arctan\left(\frac{27\sqrt{10815}}{67}\right)\right]\right)\right)\\ a = \frac{1 + \alpha}{4},\ b = \frac{1 + \beta}{4},\ c = \frac{1 + 2\gamma}{4}\\ \gamma = \sqrt{1/t},\ C = t^2/7!,\ \alpha \gt 0\\ A\alpha^2 + B\beta^2 = (1-t/21)/5!\\ A\alpha^3 + B \beta^3 = -2/6!\\ A\alpha^4 + B\beta^4 = 10/7!\\ A\alpha^5 + B\beta^5 = -6 / 7!\\ \end{cases} }[/math] [math]\displaystyle{ A \approx 0.01878132095300264180 }[/math] [math]\displaystyle{ B \approx 0.01224884051939365826 }[/math] [math]\displaystyle{ C \approx 0.00709100346284691107 }[/math] [math]\displaystyle{ a \approx 0.31088591926330060980 }[/math] [math]\displaystyle{ b \approx 0.09273525031089122640 }[/math] [math]\displaystyle{ c \approx 0.45449629587435035051 }[/math] |
| [math]\displaystyle{ 1 - 3a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ A }[/math] | ||||
| [math]\displaystyle{ a }[/math] | [math]\displaystyle{ 1 - 3a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ A }[/math] | ||||
| [math]\displaystyle{ a }[/math] | [math]\displaystyle{ a }[/math] | [math]\displaystyle{ 1 - 3a }[/math] | [math]\displaystyle{ A }[/math] | ||||
| [math]\displaystyle{ b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ B }[/math] | ||||
| [math]\displaystyle{ 1 - 3b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ B }[/math] | ||||
| [math]\displaystyle{ b }[/math] | [math]\displaystyle{ 1 - 3b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ B }[/math] | ||||
| [math]\displaystyle{ b }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ 1 - 3b }[/math] | [math]\displaystyle{ B }[/math] | ||||
| [math]\displaystyle{ \frac{1}{2} - c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ C }[/math] | ||||
| [math]\displaystyle{ c }[/math] | [math]\displaystyle{ \frac{1}{2} - c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ C }[/math] | ||||
| [math]\displaystyle{ c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ \frac{1}{2} - c }[/math] | [math]\displaystyle{ C }[/math] | ||||
| [math]\displaystyle{ \frac{1}{2} - c }[/math] | [math]\displaystyle{ \frac{1}{2} - c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ C }[/math] | ||||
| [math]\displaystyle{ \frac{1}{2} - c }[/math] | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ \frac{1}{2} - c }[/math] | [math]\displaystyle{ C }[/math] | ||||
| [math]\displaystyle{ c }[/math] | [math]\displaystyle{ \frac{1}{2} - c }[/math] | [math]\displaystyle{ \frac{1}{2} - c }[/math] | [math]\displaystyle{ C }[/math] |
Примечания
- ↑ Мысовских, 1981, с. 285.
- ↑ Мысовских, 1981, с. 280.
Литература
- Мысовских И. П. Интерполяционные кубатурные формулы. — Москва: Наука, 1981. — С. 336.
Ссылки
- Numerical Integration over the Triangular Domain (англ.) (недоступная ссылка). — Интегрирование по треугольному элементу. Дата обращения: 12 июня 2014. Архивировано 14 июля 2014 года.
- Numerical Integration over the Tetrahedral Domain (англ.) (недоступная ссылка). — Интегрирование по тетраэдальному элементу. Дата обращения: 12 июня 2014. Архивировано 14 июля 2014 года.