Арабские цифры

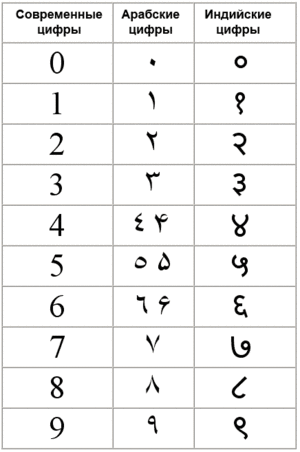
Ара́бские ци́фры (называемые также индийскими или индо-арабскими)[1] — традиционное название набора из десяти знаков (цифр), используемых в большинстве стран для записи чисел в десятичной позиционной системе счисления:
Название «арабские цифры» образовалось исторически, из-за того, что в Европу десятичная позиционная система счисления попала через арабские страны[2]. Тем не менее цифры, используемые в арабских странах Азии и в Египте (называемые арабами «индийскими цифрами»), по начертанию сильно отличаются от используемых в европейских странах.
История
-
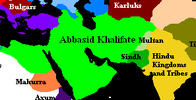
Халифат Аббасидов — территория распространения индо-арабских и персидских цифр
-
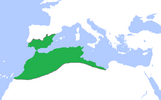
Халифат Альмохадов — территория, откуда арабские цифры попали в Европу

Индо-арабские цифры возникли в Индии не позднее V века[3]. Эта цифровая система была основана на принципах, проверенных всей предыдущей историей развития цифр — десятеричного, позиционного, принципа представления числовых значений и на использовании знака «ноль» для обозначения отсутствия цифры[4].
Первая дошедшая до наших дней запись в десятичной позиционной системе относится к 595 году н. э. Отдельного знака для нуля сначала у индийцев не было, вместо него оставляли пустое место. Символ нуля (шунья) окончательно оформился в IX веке[5].
Преимущества индийской системы записи для арифметических расчётов вскоре оценили персы и арабы. Индийские цифры активно популяризировал в IX веке при дворе халифа аль-Мансура в Багдаде хорезмиец Аль-Хорезми, автор знаменитой работы «Китаб аль-джебр ва-ль-мукабала», от названия которой произошёл термин «алгебра». Аль-Хорезми написал книгу «Об индийском счёте», которая способствовала популяризации десятичной позиционной системы записи чисел во всём Халифате, вплоть до мусульманской Испании[6].
Сохранились трактат математика Ас-Сиджизи, датированный 969 годом, и копия трактата астронома Аль-Бируни, датированная 1082 годом, содержащие индийские цифры[7].
В современных арабских странах Азии, а также в Египте, Иране, Пакистане и Афганистане, в основном, используются цифры, мало отличающиеся от имеющихся в труде аль-Бируни. Арабы называют их «ар-кам хиндия» (أَرْقَام هِنْدِيَّة) — «индийские цифры», но европейцы чаще называют их «индо-арабскими» и «персидскими», так как в языках народов современной Индии цифры эволюционировали и теперь сильно отличаются от средневековых индийских цифр. Позднее их начертания продолжали изменяться, и в трактате западноафриканского математика Ибн аль-Банна аль-Марракуши (XIII век) уже все цифры походили на нынешние европейские (хотя четвёрка и пятёрка были повёрнуты на 90 градусов)[7]. В современных арабских странах Африки (кроме Египта) используются те же цифры, что и в Европе.
Арабские цифры стали известны европейцам в X веке[6]. Первое их описание содержит «Вигиланский кодекс» (Испания, X век), причём ноль ещё не упоминается[8]. В других странах Западной Европы история индоарабских цифр начинается с XII века, а их широкое применение в Западной Европе — с XIII—XIV веков[9].
В XII веке книга Аль-Хорезми «Об индийском счёте» была переведена Робертом Честерским на латинский язык и сыграла очень большую роль в развитии европейской арифметики и внедрении арабских цифр[10].
После отвоевания Испании контакты европейцев с арабами ослабли и многие европейцы по-прежнему использовали римские цифры. Итальянский математик Фибоначчи, изучавший в 1192—1200 годах математику в Алжире и других арабских странах, снова привлёк внимание европейцев к арабским цифрам, написав «Книгу абака»[11]. В эпоху Возрождения возрос интерес к арабской науке, итальянские математики привозили в Европу арабские рукописи. Ко времени распространения книгопечатания в западноевропейской науке укоренилось западно-арабское начертание цифр.
В России арабские цифры появились в XIV—XV вв., широкое распространение получили с XVII в., а после введения гражданской азбуки в XVIII в. вытеснили из гражданской печати славяно-кирилловские цифры[4].
Преимущества индо-арабских цифр
Реализованная с помощью индо-арабских цифр десятичная позиционная система счисления постепенно вытеснила римские цифры и другие непозиционные системы нумерации благодаря множеству несомненных преимуществ[12].
- Индийская запись чисел компактнее римской и позволяет быстро сравнивать разные числа по величине.
- При расчётах на абаке можно одновременно записывать числа и проводить расчёты.
- Вычисления стало возможно проводить без абака, на бумаге. Появились новые, более простые методы умножения и деления, специально рассчитанные на индоарабские цифры.
- Вычислительная математика и математика вообще получили мощный импульс к развитию. Например, трудно представить изобретение логарифмов без индоарабских цифр.
- Благодаря им появилась возможность создания счётных машин.
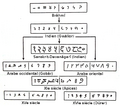
Версии написания цифр
| Арабские цифры, используемые в арабских странах Африки (кроме Египта) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Индо-арабские цифры, используемые в арабских странах Азии и в Египте | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Персидские цифры | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| Индийские цифры (в письме деванагари), используемые в Индии | ० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| Цифры в письме гуджарати | ૦ | ૧ | ૨ | ૩ | ૪ | ૫ | ૬ | ૭ | ૮ | ૯ |
| Цифры в письме гурмукхи | ੦ | ੧ | ੨ | ੩ | ੪ | ੫ | ੬ | ੭ | ੮ | ੯ |
| Цифры в бенгальском письме | ০ | ১ | ২ | ৩ | ৪ | ৫ | ৬ | ৭ | ৮ | ৯ |
| Цифры в письме ория | ୦ | ୧ | ୨ | ୩ | ୪ | ୫ | ୬ | ୭ | ୮ | ୯ |
| Цифры в письме телугу | ౦ | ౧ | ౨ | ౩ | ౪ | ౫ | ౬ | ౭ | ౮ | ౯ |
| Цифры в письме каннада | ೦ | ೧ | ೨ | ೩ | ೪ | ೫ | ೬ | ೭ | ೮ | ೯ |
| Цифры в письме малаялам | ൦ | ൧ | ൨ | ൩ | ൪ | ൫ | ൬ | ൭ | ൮ | ൯ |
| Цифры в тамильском письме | ೦ | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
| Цифры в тибетском письме | ༠ | ༡ | ༢ | ༣ | ༤ | ༥ | ༦ | ༧ | ༨ | ༩ |
| Цифры в монгольском письме | ᠐ | ᠑ | ᠒ | ᠓ | ᠔ | ᠕ | ᠖ | ᠗ | ᠘ | ᠙ |
| Цифры в бирманском письме | ၀ | ၁ | ၂ | ၃ | ၄ | ၅ | ၆ | ၇ | ၈ | ၉ |
| Цифры в тайском письме | ๐ | ๑ | ๒ | ๓ | ๔ | ๕ | ๖ | ๗ | ๘ | ๙ |
| Цифры в кхмерском письме | ០ | ១ | ២ | ៣ | ៤ | ៥ | ៦ | ៧ | ៨ | ៩ |
| Цифры в лаосском письме | ໐ | ໑ | ໒ | ໓ | ໔ | ໕ | ໖ | ໗ | ໘ | ໙ |
| Кандзи, соответствующие цифрам | 零〇 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 |
Галерея
-
Современная арабская телефонная клавиатура с двумя формами арабских цифр: западные арабские/европейские цифры слева и восточно-арабские цифры справа
-
Заимствование индийских цифр через арабов по Европе
-
Гравюра на дереве, показывающая астрономические часы XVI века Упсальского собора, с двумя видами часов, одни с арабским и другие с римскими цифрами.
-
На немецкой странице рукописи, использующей арабские цифры (Talhoffer Thott, 1459). В это время знание цифр всё ещё широко рассматривалось как эзотерическое, и Тальхоффер представляет еврейский алфавит и астрологию.
-
Французский революционный «десятичный» циферблат XVIII века.
-
Железная плита с магическим квадратом 6x6 на персидском / арабском языке из Китая, датированная династией Юань (1271-1368).
Примечания
- ↑ Цифры // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 826—827.
- ↑ Андронов И. К. Арифметика. Развитие понятия числа и действий над числами. — Учпедгиз, 1959. — С. 28—30. — 361 с.
- ↑ Bulliet, Richard. The Earth and Its Peoples: A Global History, Volume 1 / Richard Bulliet, Pamela Crossley, Daniel Headrick … [и др.]. — Cengage Learning, 2010. — P. 192. — «Indian mathematicians invented the concept of zero and developed the "Arabic" numerals and system of place-value notation used in most parts of the world today». — ISBN 1439084742. Архивная копия от 28 января 2017 на Wayback Machine
- ↑ 4,0 4,1 Истрин В.А. Развитие письма / Ред. Вентцель Т.В.. — М.: АН СССР, 1961. — С. 330—331.
- ↑ История математики, том I, 1970, с. 182—183.
- ↑ 6,0 6,1 Меннингер, 2011, с. 476—477.
- ↑ 7,0 7,1 J. J. O’Connor and E. F. Robertson. The Arabic numeral system. http://www-history.mcs.st-andrews.ac.uk/HistTopics/Arabic_numerals.html Архивная копия от 16 мая 2017 на Wayback Machine
- ↑ Florian Cajori. A history of mathematical notations. — 1993. — P. 50. — 385 p. — ISBN 0486677664.
- ↑ История математики, том I, 1970, с. 256—257.
- ↑ Юшкевич А. П. История математики в средние века. — М.: Гос. изд-во физико-математической литературы, 1961. — С. 156, 191, 331.
- ↑ Меннингер, 2011, с. 493—494.
- ↑ Меннингер, 2011, с. 508—515.
Литература
- [bse.sci-lib.com/article067055.html «Арабские цифры» в Большой советской энциклопедии]
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — 352 с.
- Меннингер К. История цифр. Числа, символы, слова. — М.: ЗАО Центрполиграф, 2011. — 543 с. — ISBN 9785952449787.
Ссылки
- Арабские цифры, использующиеся при датировке ковров
- O'Connor J. J., Robertson E. F. Indian numerals. MacTutor.