Вписанная окружность

Окружность называют вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех его сторон.

В многоугольнике

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех внутренних углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.

Радиус вписанной в многоугольник окружности равен отношению его площади [math]\displaystyle{ S }[/math] к его полупериметру [math]\displaystyle{ p }[/math]:

[math]\displaystyle{ r=\frac{S}{p} }[/math]

В треугольнике

Свойства вписанной окружности:

В каждый треугольник можно вписать окружность, притом только одну.
Центр [math]\displaystyle{ I }[/math] вписанной окружности равноудалён от всех сторон и является точкой пересечения биссектрис треугольника.
Радиус [math]\displaystyle{ r }[/math] вписанной в треугольник окружности равен:

[math]\displaystyle{ r = \sqrt{\frac{(-a+b+c)(a-b+c)(a+b-c)}{4(a+b+c)}}; }[/math]

[math]\displaystyle{ \frac{1}{r} = \frac{1}{h_a} + \frac{1}{h_b} + \frac{1}{h_c} }[/math]

где [math]\displaystyle{ a, b, c }[/math] — стороны треугольника, [math]\displaystyle{ h_a, h_b, h_c }[/math] — высоты, проведённые к соответствующим сторонам^[1];

[math]\displaystyle{ r=\frac{S}{p}=\sqrt{\frac{(p-a)(p-b)(p-c)}{p}} }[/math]

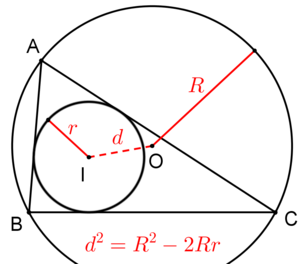
где [math]\displaystyle{ S }[/math] — площадь треугольника, а [math]\displaystyle{ p }[/math] — его полупериметр.

[math]\displaystyle{ r= \frac{p-a}{\operatorname{ctg}(\alpha/2)} = \frac{p-b}{\operatorname{ctg}(\beta/2)} = \frac{p-c}{\operatorname{ctg}(\gamma/2)} }[/math], [math]\displaystyle{ p }[/math] — полупериметр треугольника (Теорема котангенсов).

Если [math]\displaystyle{ AB }[/math] — основание равнобедренного треугольника [math]\displaystyle{ \triangle ABC }[/math], то окружность, касающаяся сторон угла [math]\displaystyle{ \angle ACB }[/math] в точках [math]\displaystyle{ A }[/math] и [math]\displaystyle{ B }[/math], проходит через центр вписанной окружности треугольника [math]\displaystyle{ \triangle ABC }[/math].
Теорема Эйлера: [math]\displaystyle{ R^2-2Rr=|OI|^2 }[/math], где [math]\displaystyle{ R }[/math] — радиус описанной вокруг треугольника окружности, [math]\displaystyle{ r }[/math] — радиус вписанной в него окружности, [math]\displaystyle{ O }[/math] — центр описанной окружности, [math]\displaystyle{ I }[/math] — центр вписанной окружности.
Если прямая, проходящая через точку I параллельно стороне [math]\displaystyle{ AB }[/math], пересекает стороны [math]\displaystyle{ BC }[/math] и [math]\displaystyle{ CA }[/math] в точках [math]\displaystyle{ A_1 }[/math] и [math]\displaystyle{ B_1 }[/math], то [math]\displaystyle{ A_1B_1=A_1B+AB_1 }[/math].
Если точки касания вписанной в треугольник [math]\displaystyle{ T }[/math] окружности с его сторонами соединить отрезками, то получится треугольник [math]\displaystyle{ T_1 }[/math] со свойствами:
- Биссектрисы T являются серединными перпендикулярами T₁
- Пусть T₂ — ортотреугольник T₁. Тогда его стороны параллельны сторонам исходного треугольника T.
- Пусть T₃ — серединный треугольник T₁. Тогда биссектрисы T являются высотами T₃.
- Пусть T₄ — ортотреугольник T₃, тогда биссектрисы T являются биссектрисами T₄.
Радиус вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c окружности равен [math]\displaystyle{ \frac{a+b-c}{2}=\frac{ab}{a+b+c} }[/math].
Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны, равно [math]\displaystyle{ d=\frac{a+b-c}{2}=p-c }[/math].
Расстояние от вершины C до центра вписанной окружности равно [math]\displaystyle{ l_c=\frac{r}{\sin(\frac{\gamma}{2})} }[/math], где [math]\displaystyle{ r }[/math] — радиус вписанной окружности, а γ — угол вершины C.
Расстояние от вершины C до центра вписанной окружности может также быть найдено по формулам [math]\displaystyle{ l_c = \sqrt{(p-c)^2 + r^2} }[/math] и [math]\displaystyle{ l_c = \sqrt{ab - 4Rr} }[/math]
Теорема о трезубце или теорема трилистника: Если D — точка пересечения биссектрисы угла A с описанной окружностью треугольника ABC, I и J — соответственно центры вписанной и вневписанной окружности, касающейся стороны BC, тогда [math]\displaystyle{ |DI|=|DB|=|DC|=|DJ| }[/math].

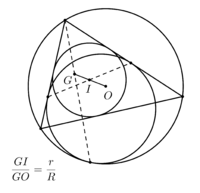
Лемма Веррьера^[2]^[3]: пусть окружность [math]\displaystyle{ V }[/math] касается сторон [math]\displaystyle{ AB }[/math], [math]\displaystyle{ AC }[/math] и дуги [math]\displaystyle{ BC }[/math] описанной окружности треугольника [math]\displaystyle{ ABC }[/math]. Тогда точки касания окружности [math]\displaystyle{ V }[/math] со сторонами и центр вписанной окружности треугольника [math]\displaystyle{ ABC }[/math] лежат на одной прямой.

Теорема Фейербаха. Окружность девяти точек касается всех трёх вневписанных окружностей, а также вписанной окружности. Точка касания окружности Эйлера и вписанной окружности известна как точка Фейербаха.

Связь вписанной и описанной окружностей

Формула Эйлера: Если [math]\displaystyle{ d }[/math] — расстояние между центрами вписанной и описанной окружностей, а их радиусы равны [math]\displaystyle{ r }[/math] и [math]\displaystyle{ R }[/math] соответственно, то [math]\displaystyle{ d^2 = R^2 - 2Rr }[/math].
Формулы для отношения и произведения радиусов:

[math]\displaystyle{ \frac{r}{R} = \frac{4 S^{2}}{pabc} = \cos \alpha + \cos \beta + \cos \gamma -1; }[/math]^[4]

[math]\displaystyle{ 2Rr = \frac{abc}{a+b+c} }[/math],

[math]\displaystyle{ \frac {r}{R} = 4\sin\frac {\alpha}{2}\sin\frac {\beta}{2}\sin\frac {\gamma}{2} = \cos\alpha + \cos\beta + \cos\gamma - 1 }[/math]

где [math]\displaystyle{ p }[/math] — полупериметр треугольника, [math]\displaystyle{ S }[/math] — его площадь.

Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности^[5].

Для треугольника можно построить полувписанную окружность, или окружность Варьера. Это окружность, касающаяся двух сторон треугольника и его описанной окружности внутренним образом. Отрезки, соединяющие вершины треугольника и соответствующие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке. Эта точка служит центром гомотетии с положительным коэффициентом, переводящей описанную окружность во вписанную.
Центр вписанной окружности лежит на отрезке, соединяющем точки касания сторон треугольника и полувписанной окружности.

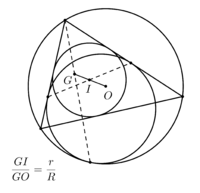
Связь центра вписанной окружности и середин высот треугольника

Теорема Ригби. Если к любой стороне остроугольного треугольника провести высоту и касающуюся ее с другой стороны вневписанную окружность, то точка касания последней с этой стороной, середина упомянутой высоты, а также инцентр лежат на одной прямой.^[6].
Из теоремы Ригби следует, что 3 отрезка, соединяющих середину каждой из 3 высот треугольника с точкой касания вневписанной окружности, проведенной к той же стороне, что и высота, пересекаются в инцентре.

В четырёхугольнике

Описанный четырёхугольник, если у него нет самопересечений («простой»), должен быть выпуклым.
Некоторые (но не все) четырёхугольники имеют вписанную окружность. Они называются описанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важным является то, что суммы противоположных сторон равны. Это утверждение называется теоремой Пито.
Иными словами, в выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны: [math]\displaystyle{ AB + CD = BC + AD }[/math].

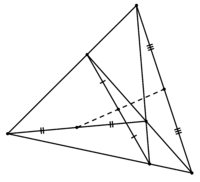
Во всяком описанном четырёхугольнике две середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона). На ней же лежит середина отрезка с концами в точках пересечения продолжений противоположных сторон четырёхугольника (если они не параллельны). Эта прямая называется прямой Ньютона. На рисунке она зелёная, диагонали красные, отрезок с концами в точках пересечения продолжений противоположных сторон четырёхугольника тоже красный.
Центр описанной около четырёхугольника окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон (теорема Брокара).

В сферическом треугольнике

Вписанная окружность для сферического треугольника — это окружность, касающаяся всех его сторон.

Тангенс радиуса^[7] вписанной в сферический треугольник окружности равен^[8]^:73-74

[math]\displaystyle{ \operatorname{tg}r=\sqrt{\frac{\sin (p-a)\sin (p-b)\sin (p-c)}{\sin p}} }[/math]

Вписанная в сферический треугольник окружность принадлежит сфере. Радиус, проведенный из центра сферы через центр вписанной окружности пересечет сферу в точке пересечения биссектрис углов (дуг больших кругов сферы, делящих углы пополам) сферического треугольника^[8]^:20-21.

Обобщения

Вписанной сферой называется сфера, касающаяся всех граней многогранника.
Эллипс Штейнера — вписанный в треугольник эллипс.

См. также

Примечания

↑ Altshiller-Court, 1925, p. 79.
↑ Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — С. 130. — 334 с.
↑ Ефремов Д. Новая геометрия треугольника. Изд. 2. Серия: Физико-математическое наследие (репринтное воспроизведение издания).. — Москва: Ленанд, 2015. — 352 с. — ISBN 978-5-9710-2186-5.
↑ Longuet-Higgins, Michael S., «On the ratio of the inradius to the circumradius of a triangle», Mathematical Gazette 87, March 2003, 119—120.
↑ Мякишев А. Г. Элементы геометрии треугольника. Серия: «Библиотека „Математическое просвещение“». М.: МЦНМО, 2002. c. 11, п. 5
↑ Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: The Mathematical Association of America, 1996, ISBN 978-0883856390. p. 30, Figure 34, §3. An Unlikely Collinearity.
↑ Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведенного из центра сферы через центр окружности, со сферой и точку касания окружностью стороны треугольника.
↑ ^8,0 ^8,1 Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.

Литература

Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 89. — 383 с. — ISBN 5-09-001287-3.
Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 52-53. — ISBN 5-94057-170-0.
Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble

[_8405234f79e9969e-1] Altshiller-Court, 1925, p. 79.

[2] Ефремов Д. Новая геометрия треугольника. — Одесса, 1902. — С. 130. — 334 с.

[3] Ефремов Д. Новая геометрия треугольника. Изд. 2. Серия: Физико-математическое наследие (репринтное воспроизведение издания).. — Москва: Ленанд, 2015. — 352 с. — ISBN 978-5-9710-2186-5.

[LH-4] Longuet-Higgins, Michael S., «On the ratio of the inradius to the circumradius of a triangle», Mathematical Gazette 87, March 2003, 119—120.

[5] Мякишев А. Г. Элементы геометрии треугольника. Серия: «Библиотека „Математическое просвещение“». М.: МЦНМО, 2002. c. 11, п. 5

[6] Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: The Mathematical Association of America, 1996, ISBN 978-0883856390. p. 30, Figure 34, §3. An Unlikely Collinearity.

[7] Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведенного из центра сферы через центр окружности, со сферой и точку касания окружностью стороны треугольника.

[St-8] 8,0 ^8,1 Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]