Ортотреугольник

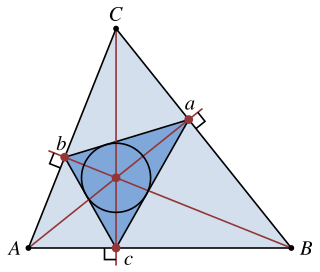
Ортотреуго́льник (ортоцентрический треугольник) — это треугольник Δabc, вершины которого являются основаниями высот треугольника ∆ABC. Для ортотреуго́льника (для ортоцентрического треугольника) Δabc сам треугольник ∆ABC является треугольником трёх внешних биссектрис. То есть отрезки AB, BC и CA являются тремя внешними биссектрисами треугольника Δabc.

Свойства

• Задача Фаньяно: ортоцентрический треугольник остроугольного треугольника АВС обладает наименьшим периметром из всех вписанных треугольников.
• Высоты остроугольного треугольника являются биссектрисами углов его ортотреугольника (следовательно ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник).
• Если точки A₁, B₁ и C₁ на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что

[math]\displaystyle{ \angle BA_1 C_1 = \angle CA_1 B_1 }[/math] , [math]\displaystyle{ \angle CB_1 A_1 = \angle AB_1 C_1 }[/math] и [math]\displaystyle{ \angle AC_1 B_1 = \angle BC_1 A_1 }[/math],

то [math]\displaystyle{ A_1 B_1 C_1 }[/math] — ортотреугольник треугольника ABC.

• Если вокруг данного остроугольного треугольника описать окружность и в трех вершинах треугольника провести прямые, касательные к окружности, то пересечение этих прямых образует треугольник, который называют тангенциальным треугольником по отношению к данному треугольнику.

Свойства подобия родственных треугольников

• Исходный треугольник [math]\displaystyle{ \Delta ABC }[/math] по отношению к ортотреугольнику является треугольником трех внешних биссектрис.

[math]\displaystyle{ \triangle A_1B_1C_1 }[/math] — ортотреугольник треугольника [math]\displaystyle{ \triangle ABC }[/math], а [math]\displaystyle{ \triangle A_2B_2C_2 }[/math]— треугольник Жергонна ортотреугольника. [math]\displaystyle{ H }[/math]— ортоцентр [math]\displaystyle{ \triangle ABC }[/math], инцентр [math]\displaystyle{ \triangle A_1B_1C_1 }[/math]и центр описанной окружности [math]\displaystyle{ \triangle A_2B_2C_2 }[/math]. Треугольники [math]\displaystyle{ \triangle ABC }[/math] и [math]\displaystyle{ \triangle A_2B_2C_2 }[/math] подобны.

• Ортотреугольник и тангенциальный треугольник подобны (Зетель, следствие 1, § 66, с. 81).
• Треугольник Жергонна ортотреугольника и исходный треугольник подобны (см. рисунок).
• Треугольник трёх внешних биссектрис треугольника трех внешних биссектрис и исходный треугольник подобны.
• Ортотреугольник треугольника Жергонна и исходный треугольник подобны.
• Выше указанные свойства подобия родственных треугольников являются следствием ниже перечисленных свойств параллельности (антипараллельности) сторон родственных треугольников.

Свойства параллельности (антипараллельности) сторон родственных треугольников

• Стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат.
• Стороны тангенциального треугольника антипараллельны соответствующим противоположным сторонам данного треугольника (по свойству антипараллельности касательных к окружности).
• Стороны тангенциального треугольника параллельны соответствующим сторонам ортотреугольника.
• Если точки касания вписанной в данный треугольник окружности соединены отрезками, то получится треугольник Жергонна. Пусть в полученном треугольнике проведены высоты. Тогда прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно, ортотреугольник треугольника Жергонна и исходный треугольник подобны.

Другие свойства

• Площадь ортотреугольника равна:

[math]\displaystyle{ S_{ort}=\frac{S}{(2abc)^2}(a^2+b^2-c^2)(a^2+c^2-b^2)(b^2+c^2-a^2) }[/math]

где [math]\displaystyle{ S }[/math] — площадь треугольника ΔABC; [math]\displaystyle{ a, b, c }[/math] — его соответствующие стороны.

• Окружность, описанная около ортотреугольника Δabc, для самого треугольника ΔABC является окружностью Эйлера (окружностью 9 точек), то есть одновременно проходит, через 3 основания медиан последнего. Заметим, что эти 3 основания медиан являются вершинами дополнительного треугольника для треугольника ΔABC.
• Радиусы окружности, описанной около данного треугольника ΔABC, проведенные через его вершины, перпендикулярны соответственным сторонам ортотреугольника Δabc (Зетель, следствие 2, § 66, с. 81).

Литература

• Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 38-39. — ISBN 5-94057-170-0.
• Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. 153 с.