Теорема Пито

PA = PB

Описанный четырёхугольник
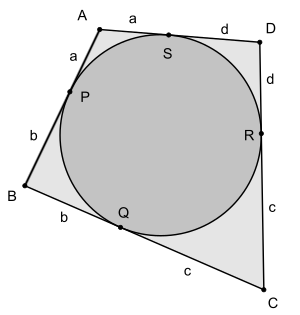
[math]\displaystyle{ \begin{align} &\quad \overline{AB} + \overline{CD}\\ &=a+b+c+d\\&=b+c+a+d\\&=\overline{BC} + \overline{DA} \end{align} }[/math]

Теорема Пито, названная именем французского инженера Анри Пито, утверждает, что у описанного четырёхугольника (т.е. четырёхугольника, в который можно вписать окружность) суммы длин противоположных сторон равны.

Теорема является следствием факта, что два касательных отрезка из одной точки, находящейся вне окружности, имеют одинаковую длину. Имеется четыре пары равных касательных отрезков и обе суммы могут быть разложены в суммы этих четырёх длин отрезков. Обратное также верно — окружность может быть вписана в любой выпуклый четырёхугольник, в котором суммы длин противоположных сторон равны.

Анри Пито доказал свою теорему в 1725, а обратную теорему доказал швейцарский математик Якоб Штейнер в 1846.

См. также

• Теорема об описанном четырёхугольнике и вписанные окружности

Литература

• Martin Josefsson. More characterizations of Tangential Quadrilaterals // Forum Geometricorum. — 2011. — Т. 11. — С. 65–82.

Ссылки

• Alexander Bogomolny, "When A Quadrilateral Is Inscriptible?" at Cut-the-knot