Уравнение синус-Гордона

Уравнение синус-Гордона — это нелинейное гиперболическое уравнение в частных производных в 1 + 1 измерениях, включающее в себя оператор Даламбера и синус неизвестной функции. Изначально оно было рассмотрено в XIX веке в связи с изучением поверхностей постоянной отрицательной кривизны. Это уравнение привлекло много внимания в 1970-х годах из-за наличия у него солитонных решений.

Происхождение уравнения и его названия

Существует две эквивалентные формы уравнения синус-Гордона. В (вещественных) координатах пространство-время, обозначенных (x, t), уравнение имеет вид

[math]\displaystyle{ \varphi_{tt} - \varphi_{xx} + \sin\varphi = 0. }[/math]

При переходе к координатам светового конуса (u, v), близким к асимптотическим координатам, где

[math]\displaystyle{ u = \frac{x + t}{2}, \quad v = \frac{x - t}{2}, }[/math]

уравнение принимает вид

[math]\displaystyle{ \varphi_{uv} = \sin\varphi. }[/math]

Это исходная форма уравнения синус-Гордона, в которой оно было рассмотрено в XIX веке в связи с изучением поверхностей постоянной гауссовой кривизны K = −1, также называемых псевдосферами. Выберем систему координат, в которой координатная сетка u = const, v = const задаётся асимптотическими линиями, параметризованными длиной дуги. Первая квадратичная форма данной поверхности в таких координатах примет специальный вид:

[math]\displaystyle{ ds^2 = du^2 + 2\cos\varphi \,du\,dv + dv^2, }[/math]

где φ — угол между асимптотическими линиями, и для второй квадратичной формы, L = N = 0. Тогда уравнение Петерсона ― Кодацци, отражающее условие совместимости между первой и второй квадратичными формами, приводит к уравнению синус-Гордона. Изучение этого уравнения и соответствующих преобразований псевдосфер в XIX веке Бьянки и Бэклундом привели к открытию преобразований Бэклунда.

Название «уравнение синус-Гордона» — каламбур на тему хорошо известного в физике уравнения Клейна — Гордона:

[math]\displaystyle{ \varphi_{tt} - \varphi_{xx} + \varphi = 0. }[/math]

Уравнение синус-Гордона является уравнением Эйлера — Лагранжа для лагранжиана

[math]\displaystyle{ \mathcal{L}_\text{sine-Gordon}(\varphi) := \frac{1}{2}(\varphi_t^2 - \varphi_x^2) - 1 + \cos\varphi. }[/math]

Используя разложение в ряд Тейлора косинуса

[math]\displaystyle{ \cos(\varphi) = \sum_{n=0}^\infty \frac{(-\varphi ^2)^n}{(2n)!} }[/math]

в данном лагранжиане, он может быть записан как лагранжиан Клейна — Гордона плюс члены более высокого порядка

[math]\displaystyle{ \begin{align} \mathcal{L}_\text{sine-Gordon}(\varphi) & = \frac{1}{2}(\varphi_t^2 - \varphi_x^2) - \frac{\varphi^2}{2} + \sum_{n=2}^\infty \frac{(-\varphi^2)^n}{(2n)!} = \\ & = 2\mathcal{L}_\text{Klein–Gordon}(\varphi) + \sum_{n=2}^\infty \frac{(-\varphi^2)^n}{(2n)!}. \end{align} }[/math]

Солитоны

Интересное свойство уравнения синус-Гордона — существование солитонных и многосолитонных решений.

Односолитонное решение

Уравнение синус-Гордона имеет следующие односолитонные решения:

[math]\displaystyle{ \varphi_\text{soliton}(x, t) := 4 \arctan e^{m \gamma (x - v t) + \delta}, }[/math]

где

[math]\displaystyle{ \gamma^2 = \frac{1}{1 - v^2}. }[/math]

Односолитонное решение, для которого мы выбрали положительный корень для [math]\displaystyle{ \gamma }[/math], называется кинк и представляет виток по переменной [math]\displaystyle{ \varphi }[/math], который переводит одно решение [math]\displaystyle{ \varphi = 0 }[/math] в смежное [math]\displaystyle{ \varphi = 2\pi }[/math]. Состояния [math]\displaystyle{ \varphi = 0 \pmod{2\pi} }[/math] известны как вакуумные, так как они являются постоянными решениями нулевой энергии. Односолитонное решение, в котором мы взяли отрицательный корень для [math]\displaystyle{ \gamma }[/math], называется антикинк. Форма односолитонных решений может быть получена посредством применения преобразования Бэклунда к тривиальному (постоянному вакуумному) решению и интегрированию получившихся дифференциальных уравнений первого порядка:

[math]\displaystyle{ \varphi'_u = \varphi_u + 2\beta\sin\frac{\varphi' + \varphi}{2}, }[/math]

[math]\displaystyle{ \varphi'_v = -\varphi_v + \frac{2}{\beta} \sin\frac{\varphi' - \varphi}{2}, \quad \varphi = \varphi_0 = 0. }[/math]

Односолитонные решения могут быть визуализированы посредством синус-гордоновской модели упругой ленты^[1]. Примем виток упругой ленты по часовой стрелке (левовинтовой) за кинк с топологическим зарядом [math]\displaystyle{ \vartheta_\textrm{K} = -1 }[/math]. Альтернативный виток против часовой стрелки (правовинтовой) с топологическим зарядом [math]\displaystyle{ \vartheta_\textrm{AK} = +1 }[/math] будет антикинком.

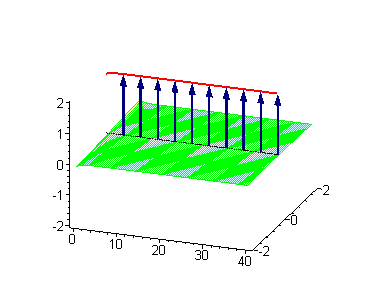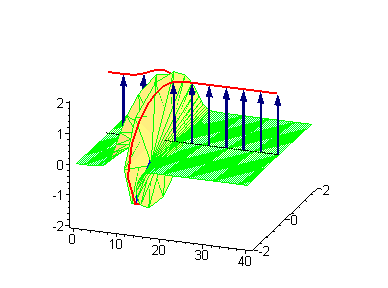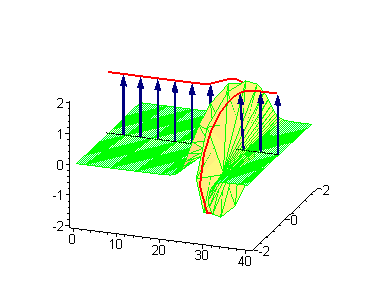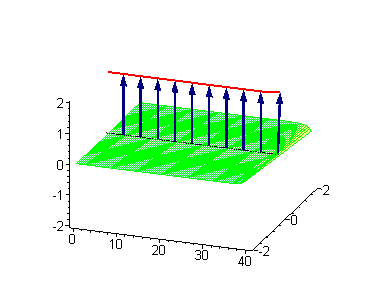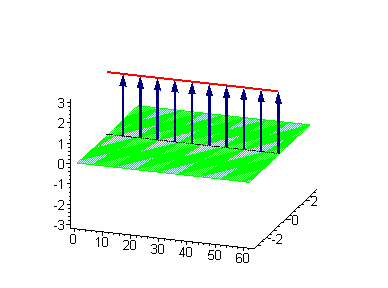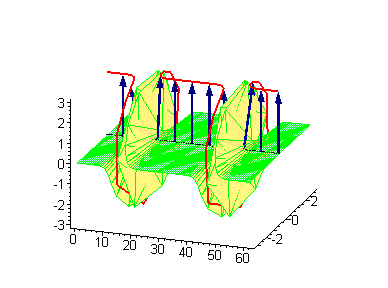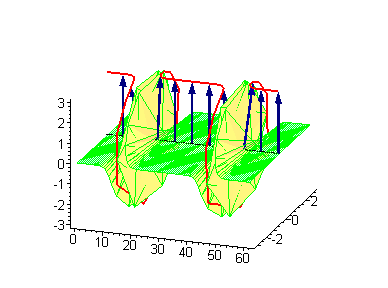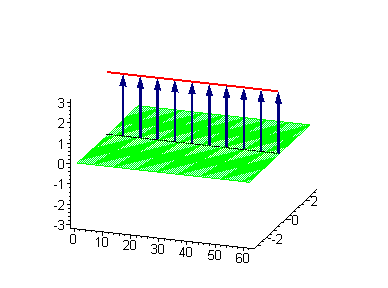
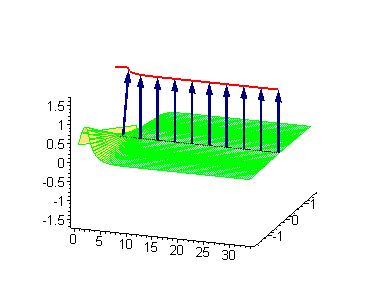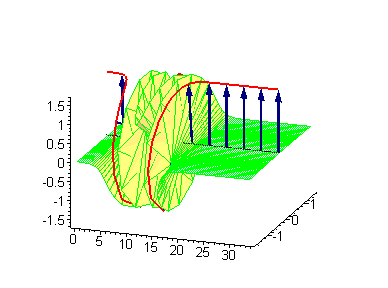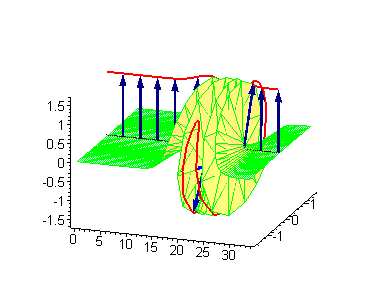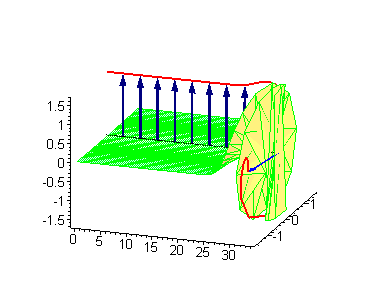
Двухсолитонные решения

Многосолитонные решения могут быть получены посредством непрерывного применения преобразования Бэклунда к односолитонному решению, как предписывается решёткой Бьянки, соответствующей результатам преобразования^[2]. 2-солитонные решения уравнения синус-Гордона проявляют некоторые характерные свойства солитонов. Бегущие синус-гордоновские кинки и/или антикинки проходят сквозь друг друга как полностью проницаемые, и единственный наблюдаемый эффект — фазовый сдвиг. Так как сталкивающиеся солитоны сохраняют свою скорость и форму, такой вид взаимодействия называется упругим столкновением.

Другие интересные двухсолитонные решения возникают из возможности спаренного кинк-антикинкового поведения, известного как бризер. Известно три типа бризеров: стоячий бризер, бегущий высокоамплитудный бризер и бегущий малоамплитудный бризер^[3].

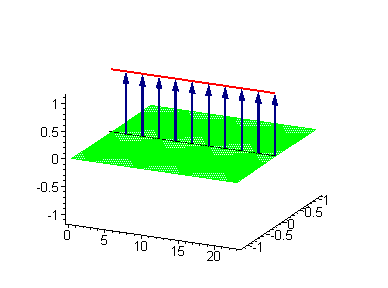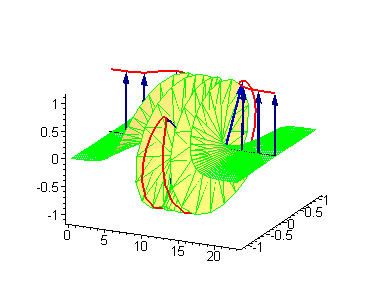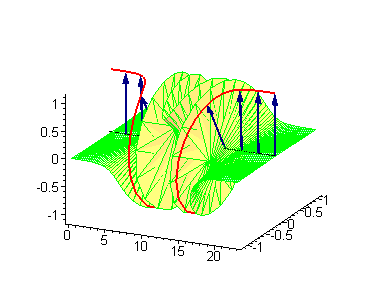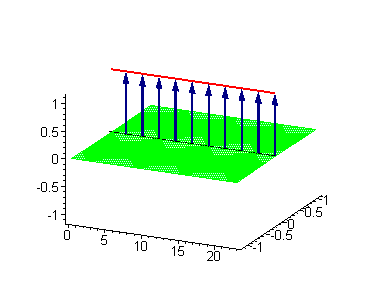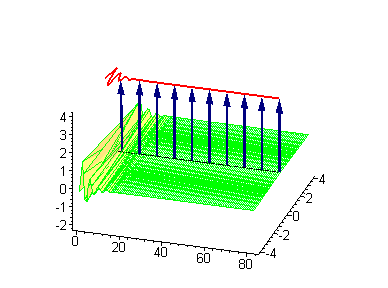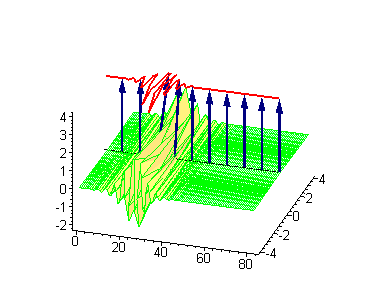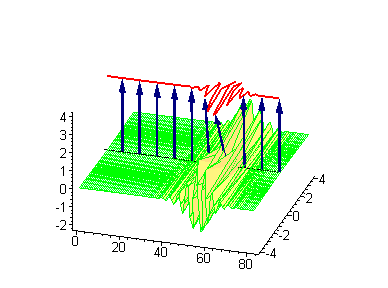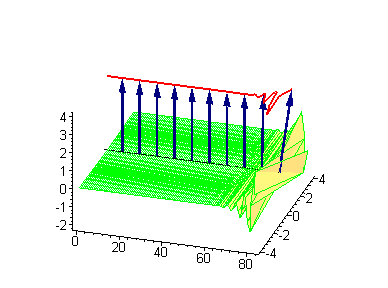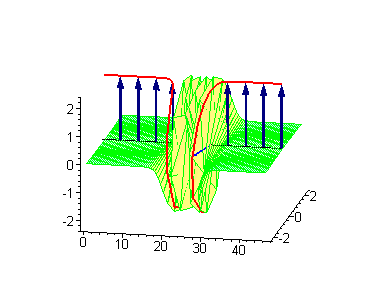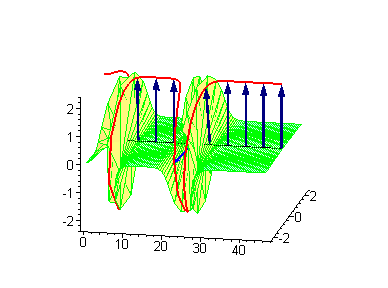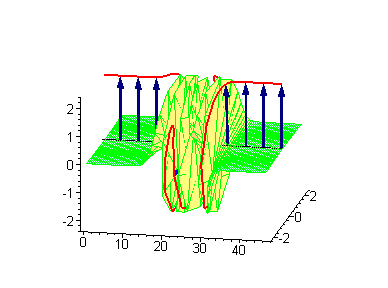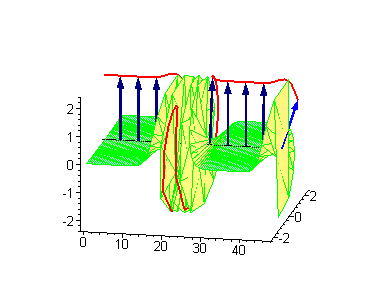
Трёхсолитонные решения

Трёхсолитонные столкновения между бегущим кинком и стоячим бризером или бегущим антикинком и стоячим бризером приводят к фазовому сдвигу стоячего бризера. В процессе столкновения между движущимся кинком и стоячим бризером сдвиг последнего [math]\displaystyle{ \Delta_\textrm{B} }[/math] даётся соотношением

[math]\displaystyle{ \Delta_B = \frac{2\operatorname{arctanh}\sqrt{(1 - \omega^{2})(1 - v_\text{K}^2)}}{\sqrt{1 - \omega^{2}}}, }[/math]

где [math]\displaystyle{ v_\text{K} }[/math] — скорость кинка, а [math]\displaystyle{ \omega }[/math] — частота бризера^[3]. Если координата стоячего бризера до столкновения — [math]\displaystyle{ x_0 }[/math], то после столкновения она станет [math]\displaystyle{ x_0 + \Delta_\text{B} }[/math].

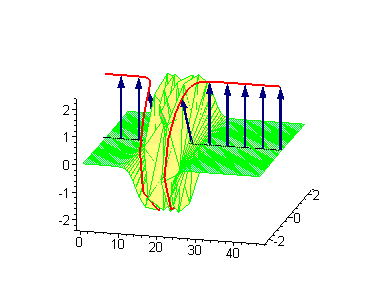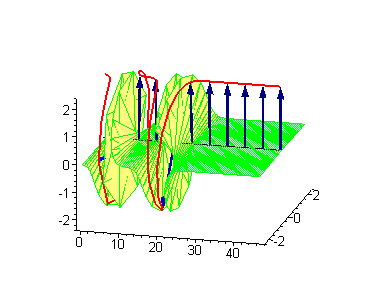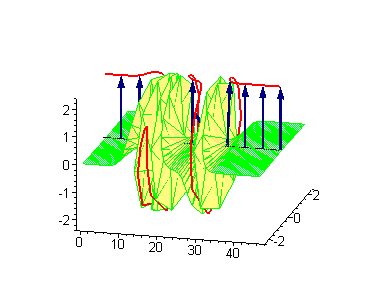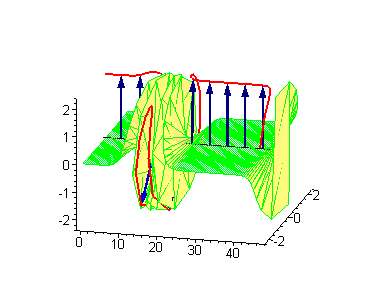Столкновение антикинка со стоящим бризером

Связанные уравнения

Уравнение шинус-Гордона^{[источник не указан 4614 дней]}:

[math]\displaystyle{ \varphi_{xx} - \varphi_{tt} = \sinh\varphi. }[/math]

Это уравнения Эйлера — Лагранжа для лагранжиана

[math]\displaystyle{ \mathcal{L} = \frac{1}{2}(\varphi_t^2 - \varphi_x^2) - \cosh\varphi. }[/math]

Другое тесно связанное с уравнением синус-Гордона — это эллиптическое уравнение синус-Гордона:

[math]\displaystyle{ \varphi_{xx} + \varphi_{yy} = \sin\varphi, }[/math]

где [math]\displaystyle{ \varphi }[/math] — функция переменных x и y. Это уже не солитонное уравнение, но оно имеет много похожих свойств, так как оно связано с уравнением синус-Гордона аналитическим продолжением (или поворотом Вика) y = it.

Эллиптическое уранение шинус-Гордона может быть определено аналогичным образом. Обобщение даётся теорией поля Тоды.

Квантовая версия

В квантовой теории поля модель синус-Гордона содержит параметр, который может быть отождествлён с постоянной Планка. Спектр частиц состоит из солитона, антисолитона и конечного (возможно, нулевого) числа бризеров. Число бризеров зависит от данного параметра. Множественные рождения частиц сокращаются на уравнениях движения.

Квазиклассическое квантование модели синус-Гордона было осуществлено Людвигом Фаддеевым и Владимиром Корепиным^[4]. Точная квантовая матрица рассеяния была открыта Александром и Алексеем Замолодчиковыми^[5]. Данная модель s-дуальна модели Тирринга.

В конечном объёме и на луче

Также рассматривают модель синус-Гордона на круге, отрезке прямой или луче. Возможно подобрать граничные условия, которые сохраняют интегрируемость данной модели. На луче спектр частиц содержит пограничные состояния кроме солитонов и бризеров.

Суперсимметричная модель синуса-Гордона

Суперсимметричный аналог модели синус-Гордона также существует. С таким же успехом для него могут быть найдены сохраняющие интегрируемость граничные условия.

Примечания

↑ Dodd R. K., Eilbeck J. C., Gibbon J. D., Morris H. C. Solitons and Nonlinear Wave Equations. Academic Press, London, 1982.
↑ Rogers C., Schief W. K. Bäcklund and Darboux Transformations. New York: Cambridge University Press, 2002.
↑ ^3,0 ^3,1 Miroshnichenko A., Vasiliev A., Dmitriev S. Solitons and Soliton Collisions Архивная копия от 22 августа 2010 на Wayback Machine.
↑ Faddeev L. D., Korepin V. E. Quantum theory of solitons (англ.) // Physics Reports. — 1978. — Vol. 42, iss. 1. — P. 1—87. — doi:10.1016/0370-1573(78)90058-3.
↑ Zamolodchikov A. B., Zamolodchikov A. B. Factorized S-matrices in two dimensions as the exact solutions of certain relativistic quantum field theory models (англ.) // Annals of Physics. — 1979-08-01. — Vol. 120, iss. 2. — P. 253—291. — doi:10.1016/0003-4916(79)90391-9.

Ссылки

Polyanin A. D., Zaitsev V. F. Handbook of Nonlinear Partial Differential Equations. Chapman & Hall / CRC Press, Boca Raton, 2004.
Rajaraman R. Solitons and instantons. North-Holland Personal Library, 1989.

[1] Dodd R. K., Eilbeck J. C., Gibbon J. D., Morris H. C. Solitons and Nonlinear Wave Equations. Academic Press, London, 1982.

[rogers-2] Rogers C., Schief W. K. Bäcklund and Darboux Transformations. New York: Cambridge University Press, 2002.

[mir-3] 3,0 ^3,1 Miroshnichenko A., Vasiliev A., Dmitriev S. Solitons and Soliton Collisions Архивная копия от 22 августа 2010 на Wayback Machine.

[4] Faddeev L. D., Korepin V. E. Quantum theory of solitons (англ.) // Physics Reports. — 1978. — Vol. 42, iss. 1. — P. 1—87. — doi:10.1016/0370-1573(78)90058-3.

[5] Zamolodchikov A. B., Zamolodchikov A. B. Factorized S-matrices in two dimensions as the exact solutions of certain relativistic quantum field theory models (англ.) // Annals of Physics. — 1979-08-01. — Vol. 120, iss. 2. — P. 253—291. — doi:10.1016/0003-4916(79)90391-9.

[1]

[2]

[3]

[4]

[5]