Кинк (математика)
Кинк — это решение уравнений поля в некоторых теориях поля в [math]\displaystyle{ 1+1 }[/math] измерениях, интерполирующее между двумя вакуумами при изменении пространственной координаты от [math]\displaystyle{ -\infty }[/math] до [math]\displaystyle{ +\infty }[/math]. Кинк является простейшим топологическим солитоном.
Кинк в модели одного действительного скалярного поля

Рассмотрим[1] теорию одного действительного скалярного поля в пространстве размерности [math]\displaystyle{ 1+1 }[/math] с действием
- [math]\displaystyle{ S=\int d^2 x \left [ \frac{1}{2} \phi_{,\mu} \phi^{,\mu} - V(\phi) \right ], }[/math]
где [math]\displaystyle{ \phi }[/math] — потенциал поля, [math]\displaystyle{ \mu = 0, 1 }[/math], а
- [math]\displaystyle{ V(\phi) = - \frac{\mu^{2}}{2} \phi^{2} + \frac{\lambda}{4} \phi^{4} + \frac{\mu^4}{4\lambda} = \frac{\lambda}{4} (\phi^{2}-v^2)^2,~~ v = \frac{\mu}{\sqrt \lambda}. }[/math]
Действие инвариантно относительно дискретного преобразования [math]\displaystyle{ \phi=-\phi }[/math]; эта симметрия спонтанно нарушается, так как классические вакуумы равны [math]\displaystyle{ \phi^{vac}=\pm v }[/math].
Из принципа наименьшего действия получается уравнение поля
- [math]\displaystyle{ \phi_{,\mu}^{~~\mu}+\frac{\partial V(\phi)}{\partial \phi}=0. }[/math]
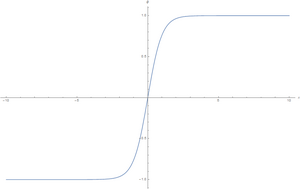
Будем искать статическое, то есть не зависящее от времени решение уравнений поля. В этом случае уравнение поля сводится к
- [math]\displaystyle{ \phi''-\frac{\partial V(\phi)}{\partial \phi}=0, }[/math]
где штрих обозначает производную по пространственной координате. Полученное уравнение имеет следующее решение:
- [math]\displaystyle{ \phi = v \tanh (\pm\sqrt{\frac{\lambda}{2}}v(x-x_0)) = \frac{\mu}{\sqrt\lambda}\tanh{(\pm\frac{\mu}{\sqrt 2}x)}, }[/math]
где [math]\displaystyle{ x_0 }[/math] — постоянная интегрирования. Данное решение и является простейшим статическим кинком, интерполирующим между вакуумами [math]\displaystyle{ -v }[/math] и [math]\displaystyle{ +v }[/math] при изменении пространственной координаты от [math]\displaystyle{ -\infty }[/math] до [math]\displaystyle{ +\infty }[/math]. Решение со знаком [math]\displaystyle{ - }[/math] называется антикинком.
Свойства решения
Размер кинка имеет порядок величины [math]\displaystyle{ r_k=\mu^{-1} }[/math], то есть порядок комптоновской длины волны элементарного возбуждения. Действительно, плотность энергии кинка
- [math]\displaystyle{ \epsilon (x)=\frac{1}{2}\phi'^2+V(\phi)=\frac{\lambda}{2} v^4 \frac{1}{\cosh^4 (\frac{\mu}{\sqrt 2} (x-x_0))} }[/math]
существенно отличается от нуля только в области [math]\displaystyle{ |x-x_0|\lesssim r_k }[/math].
Статическая энергия кинка равна
- [math]\displaystyle{ \int_{-\infty}^{\infty} \epsilon (x) dx = \frac{2}{3}m v^2, }[/math]
где [math]\displaystyle{ m=\sqrt 2 \mu }[/math] — масса элементарного возбуждения.
Полученное решение не инвариантно относительно пространственных трансляций и преобразований Лоренца. Однако эти преобразования переводят решения уравнений поля в другие решения. Применяя трансляции и преобразование Лоренца, получим следующее семейство нестатических решений:
- [math]\displaystyle{ \phi=\frac{\mu}{\sqrt\lambda}\tanh{(\pm\frac{\mu}{\sqrt 2}\frac{(x-x_0)-u t}{\sqrt{1-u^2}})}, }[/math]
где [math]\displaystyle{ u }[/math] — скорость движущегося кинка.
Кинк в модели одного комплексного скалярного поля
Рассмотрим[1] теорию одного комплексного скалярного поля в пространстве размерности [math]\displaystyle{ 1+1 }[/math] с лагранжианом
- [math]\displaystyle{ \Lambda=\phi_{,\mu} \bar{\phi}^{,\mu}+\mu^2 \phi \bar{\phi} - \frac{\lambda}{2} (\phi \bar{\phi})^2. }[/math]
Принцип наименьшего действия приводит к следующим уравнениям поля:
- [math]\displaystyle{ \phi_{,\mu}^{~~\mu}=\mu^2 \phi-\lambda \phi^2 \bar{\phi}, }[/math]
- [math]\displaystyle{ \bar{\phi}_{,\mu}^{,\mu}=\mu^2 \bar{\phi}-\lambda \bar{\phi}^2 \phi. }[/math]
Полученные уравнения имеют решением кинк из теории действительного скалярного поля
- [math]\displaystyle{ \phi=\bar{\phi}=\frac{\mu}{\sqrt\lambda}\tanh{(\pm\frac{\mu}{\sqrt 2}x)}. }[/math]
Кинк в уравнении синус-Гордона

Рассмотрим[1] теорию одного действительного скалярного поля в пространстве размерности [math]\displaystyle{ 1+1 }[/math] с лагранжианом
- [math]\displaystyle{ \Lambda=\phi_{,\mu} \phi^{,\mu}+m^2 v^2 [\cos \frac{\phi}{v}-1]. }[/math]
Принцип наименьшего действия приводит к уравнению
- [math]\displaystyle{ \phi_{,\mu}^{~~\mu}+m^2 v \sin \frac{\phi}{v}=0, }[/math]

которое заменой [math]\displaystyle{ x\rightarrow mx,~~t\rightarrow mt,~~\phi\rightarrow \frac{\phi}{v} }[/math] приводится к уравнению синус-Гордона
- [math]\displaystyle{ \phi_{tt}- \phi_{xx} + \sin\phi = 0, }[/math]
имеющему следующие частные решения[2], представляющие движущиеся со скоростью [math]\displaystyle{ v }[/math] кинки, интерполирующие между вакуумами [math]\displaystyle{ \phi_0=2 \pi k,~~ k\in\mathbb{Z} }[/math] и [math]\displaystyle{ \phi_0 + 2\pi }[/math] при изменении [math]\displaystyle{ x }[/math] от [math]\displaystyle{ -\infty }[/math] до [math]\displaystyle{ +\infty }[/math]:
- [math]\displaystyle{ \phi (x,t)=\phi_0 + 4\arctan \left \{ \exp \left [ \pm \frac{x+vt}{\sqrt{v^2-1}}+\delta \right ] \right \}, }[/math]
где [math]\displaystyle{ \delta }[/math] — произвольная постоянная. Знак [math]\displaystyle{ + }[/math] соответствует кинку, знак [math]\displaystyle{ - }[/math] — антикинку.
Примечания
Литература
- Т. И. Белова, А. Е. Кудрявцев, Солитоны и их взаимодействия в классической теории поля, УФН 167, 377—406 (1997) Архивная копия от 20 декабря 2016 на Wayback Machine.
- V.A. Gani, A.E. Kudryavtsev, M.A. Lizunova, Kink interactions in the (1+1)-dimensional φ6 model, Phys. Rev. D 89, 125009 (2014); [http://web.archive.org/web/20161220140059/https://arxiv.org/abs/1402.5903 Архивная копия от 20 декабря 2016 на Wayback Machine arXiv:1402.5903 [hep-th]].
- V.A. Gani, V. Lensky, M.A. Lizunova, Kink excitation spectra in the (1+1)-dimensional φ8 model, JHEP 08 (2015) 147; [http://web.archive.org/web/20161220135634/https://arxiv.org/abs/1506.02313 Архивная копия от 20 декабря 2016 на Wayback Machine arXiv:1506.02313 [hep-th]].