Аффинная дифференциальная геометрия
Необходимо проверить качество перевода и исправить содержательные и стилистические ошибки. |
Аффинная дифференциальная геометрия — это тип дифференциальной геометрии, в котором дифференциальные инварианты инвариантны относительно сохраняющих объем аффинных преобразований. Название аффинная дифференциальная геометрия следует из эрлангенской программы Феликса Клейна. Основное различие между аффинной и Римановой дифференциальными геометриями состоит в том, что в аффинном случае мы вводим форму объёма над многообразием вместо метрики.
Предварительное исследование
Здесь мы рассматриваем простейший случай, то есть многообразия коразмерности один. Пусть M ⊂ Rn+1 будет n-мерным многообразием, и пусть ξ — векторное поле на Rn+1 трансверсальное к M такое, что TpRn+1 = TpM ⊕ Span(ξ) для всех p ∈ M, где ⊕ обозначает прямую сумму, а Span — линейную оболочку.
Для гладкого многообразия, скажем N, пусть Ψ(N) обозначает модуль гладких векторных полей над N. Пусть D : Ψ(Rn+1)×Ψ(Rn+1) → Ψ(Rn+1) будет стандартной ковариантной производной на Rn+1 где D(X, Y) = DXY. Мы можем разложить DXY на компонент, касательный к M, и поперечный компонент — параллельные к ξ. Это дает уравнение Гаусса: DXY = ∇XY + h(X,Y)ξ, где ∇ : Ψ(M)×Ψ(M) → Ψ(M) — индуцированная связность на M и h : Ψ(M)×Ψ(M) → R является билинейной формой. Обратите внимание, что ∇ и h зависят от выбора поперечного векторного поля ξ. Мы рассматриваем только те гиперповерхности, для которых h является невырожденным[англ.]. Это свойство гиперповерхности M и не зависит от выбора поперечного векторного поля ξ.[1] Если h невырожден, мы говорим, что M невырожден. В случае кривых на плоскости невырожденные кривые — это кривые без перегибов. В случае поверхностей в трехмерном пространстве невырожденные поверхности — это поверхности без параболических точек[англ.].
Мы также можем рассматривать производную ξ в некотором касательном направлении, скажем X. Эта величина, DXξ, может быть разложена на составляющую, касательную к M, и поперечную составляющую, параллельную ξ. Это дает уравнение Вейнгартена[англ.]: DXξ = −SX + τ(X)ξ. Тензор типа-(1,1) S : Ψ(M) → Ψ(M) называется оператором аффинной формы, дифференциальная одноформа τ : Ψ(M) → R называется формой поперечной связности. Опять же, и S, и τ зависят от выбора поперечного векторного поля ξ.
Первая форма индуцированного объема
Пусть Ω : Ψ(Rn+1)n+1 → R будет формой объёма, определенной на Rn+1. Мы можем индуктировать форму объема на M, заданную через ω : Ψ(M)n → R заданную через ω(X1,...,Xn) := Ω(X1,...,Xn,ξ). Естественное определение: в Евклидовой дифференциальной геометрии, где ξ — Евклидова единичная нормаль, следует что стандартный евклидов объём охватываемый X1,…,Xn всегда равен ω(X1,…,Xn). Отметим, что ω зависит от выбора поперечного векторного поля ξ.
Вторая форма индуцированного объема
Для касательных векторов X1,…,Xn пусть H := (hi,j) будет n × n матрицей заданной через hi,j := h(Xi,Xj). Мы определяем форму второго объёма на M, задаваемую ν : Ψ(M)n → R, где ν(X1,...,Xn) := |det(H)|1⁄2. Опять же, это естественное определение. Если M = Rn и h евклидово скалярное произведение, то ν(X1,…,Xn) всегда является стандартным евклидовым объемом, охватываемым векторами X1,…,Xn. Поскольку h зависит от выбора поперечного векторного поля ξ, отсюда следует, что ν тоже.
Два естественных условия
Мы ставим два естественных условия. Во-первых, индуцированная связь ∇ и индуцированная форма объема ω совместимы, то есть ω ≡ 0. Это означает, что ∇Xω = 0 для всех X ∈ Ψ(M). Другими словами, если мы параллельно переносим векторы X1,…,Xn вдоль некоторой кривой в M относительно связи ∇, тогда объем, охватываемый X1,…,Xn по отношению к форме объема ω не изменяется. Прямое вычисление[1] показывает, что ∇Xω = τ(X)ω и поэтому ∇Xω = 0 для всех X ∈ Ψ(M), если и только если, τ ≡ 0, то есть DXξ ∈ Ψ(M) для всех X ∈ Ψ(M). Это означает, что производная ξ, в касательном направлении X относительно D всегда дает, возможно, нулевой касательный вектор к M. Второе условие состоит в том, что две формы объема ω и ν совпадают, то есть ω ≡ ν.
Вывод
Можно показать[1], что существует, с точностью до знака, единственный выбор поперечного векторного поля ξ, для которого два условия: ∇ω ≡ 0 и ω ≡ ν удовлетворены. Эти два специальных поперечных векторных поля называются аффинными нормальными векторными полями, или иногда называемые нормальными полями Бляшке.[2] Из его зависимости от формы объема для его определения мы видим, что аффинное нормальное векторное поле инвариантно относительно сохраняющих объем аффинных преобразований. Эти преобразования задаются как SL(n+1,R) ⋉ Rn+1, где SL(n+1,R) обозначает специальную линейную группу матриц (n+1) × (n+1) с действительными элементами и определителем 1, а ⋉ обозначает полупрямое произведение. SL(n+1,R) ⋉ Rn+1 образует группу Ли.
Аффинная нормальная линия
Аффинная нормальная линия в точке p ∈ M — это прямая, проходящая через p и параллельная ξ.
Плоские кривые
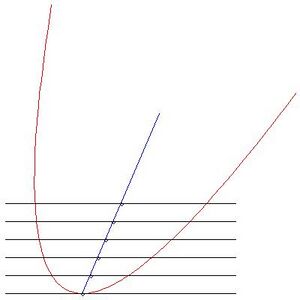
Аффинное нормальное векторное поле для кривой на плоскости имеет красивую геометрическую интерпретацию.[2] Пусть I ⊂ R будет открытым интервалом и пусть γ : I → R2 будет гладкой параметризацией плоской кривой. Мы предполагаем, что γ(I) — невырожденная кривая (в значениях Номизу и Сасаки[1]), то есть не имеет точек перегиба. Рассмотрим точку p = γ(t0) на плоской кривой. Поскольку γ(I) не имеет точек перегиба, следует, что γ(t0) не является точкой перегиба, и поэтому кривая будет локально выпуклой,[3] то есть все точки γ(t) с t0 − ε < t < t0 + ε, для достаточно малых ε , будут лежать на той же стороне касательной к γ(I) в γ(t0).
Пусть γ(t0) — касательная к γ(I) и пусть ближайшие параллельные прямые на стороне касательной содержат часть кривой P := {γ(t) ∈ R2 : t0 − ε < t < t0 + ε}. Для параллельных прямых, достаточно близких к касательной, они будут пересекать P ровно в двух точках. На каждой параллельной прямой мы отмечаем середину отрезка, соединяющего эти две точки пересечения. Для каждой параллельной прямой получаем середину, и таким образом геометрическое место точек средних точек очерчивает кривую, начинающуюся в p. Предельная касательная к геометрическому пространству средних точек по мере приближения к p — это аффинная нормальная линия, то есть прямая, содержащая вектор аффинной нормали к γ(I) в точке γ(t0). Обратите внимание, что это аффинная инвариантная конструкция, поскольку параллелизм и середины инвариантны относительно аффинных преобразований.
Рассмотрим параболу, заданную параметризацией γ(t) = (t + 2t2,t2). У этого есть уравнение x2 + 4y2 − 4xy − y = 0. Касательная в точке γ(0) имеет уравнение y = 0, и таким образом параллельные прямые заданы y = k для достаточно малых k ≥ 0. Линия y = k пересекает кривую в точке x = 2k ± √k. Расположение средних точек задается выражением {(2k,k) : k ≥ 0}. Это образует отрезок прямой, и поэтому предельная касательная к этому отрезку прямой, когда мы стремимся к γ(0), — это как раз линия, содержащая этот отрезок, то есть прямая x = 2y. В этом случае аффинная нормальная линия к кривой в точке γ(0) имеет уравнение x = 2y. Фактически, прямое вычисление показывает, что аффинный вектор нормали в точке γ(0), а именно ξ(0), задается формулой ξ(0) = 21⁄3·(2,1).[4] На рисунке красная кривая — это кривая γ, черные линии — это касательная линия и некоторые соседние касательные линии, черные точки — это середины отображаемых линий, а синяя линия — это геометрическое место средних точек.
Поверхности в трёхмерном пространстве
Похожий аналог существует для нахождения аффинной нормальной прямой в эллиптических точках[англ.] гладких поверхностей в трёхмерном пространстве. На этот раз берутся плоскости, параллельные касательной. Это, для плоскостей достаточно близких к касательной плоскости, пересекает поверхность чтобы образовать выпуклые плоские кривые. Каждая выпуклая плоская кривая имеет центр масс. Геометрическое место центров масс очерчивают кривую в трёхмерном пространстве. Предельная касательная к этому геометрическому множеству, когда геометрическое место центров масс стремится к исходной точке поверхности, является аффинной нормальной линией, то есть линией, содержащей вектор аффинной нормали.
См. также
Примечания
- ↑ 1,0 1,1 1,2 1,3 Nomizu, K. & Sasaki, T. (1994), Affine Differential Geometry: Geometry of Affine Immersions, Cambridge University Press, ISBN 0-521-44177-3, <https://archive.org/details/affinedifferenti0000nomi>
- ↑ 2,0 2,1 Su, Buchin (1983), Affine Differential Geometry, Harwood Academic, ISBN 0-677-31060-9, <https://archive.org/details/affinedifferenti0000supu>
- ↑ Bruce, J. W. & Giblin, P. J. (1984), Curves and Singularities, Cambridge University Press, ISBN 0-521-42999-4
- ↑ Davis, D. (2006), Generic Affine Differential Geometry of Curves in Rn, Proc. Royal Soc. Edinburgh, 136A, 1195−1205.
На эту статью не ссылаются другие статьи Руниверсалис. |