Атомное ядро

А́томное ядро́ — центральная часть атома, в которой сосредоточена основная его масса (более 99,9 %). Ядро заряжено положительно, заряд ядра определяет химический элемент, к которому относят атом. Размеры ядер различных атомов составляют несколько фемтометров, что более чем в 10 тысяч раз меньше размеров самого атома. Атомные ядра изучает ядерная физика.

Атомное ядро состоит из нуклонов — положительно заряженных протонов и нейтральных нейтронов, которые связаны между собой при помощи сильного взаимодействия. Протон и нейтрон обладают собственным моментом количества движения (спином), равным [math]\displaystyle{ \hbar/2 = h/ 4\pi }[/math]^{[сн 1]} и связанным с ним магнитным моментом. Единственный стабильный атом, не содержащий нейтронов в ядре — лёгкий водород (протий).

Атомное ядро, рассматриваемое как класс частиц с определённым числом протонов и нейтронов, принято называть нуклидом.

В некоторых редких случаях могут образовываться короткоживущие экзотические атомы, у которых вместо нуклона ядром служат иные частицы.

Количество протонов в ядре называется его зарядовым числом [math]\displaystyle{ Z }[/math] — это число равно порядковому номеру элемента, к которому относится атом, в таблице (Периодической системе элементов) Менделеева. Количество протонов в ядре определяет структуру электронной оболочки нейтрального атома и, таким образом, химические свойства соответствующего элемента. Количество нейтронов в ядре называется его изотопическим числом [math]\displaystyle{ N }[/math]^{[источник не указан 1961 день (обс.)]}. Ядра с одинаковым числом протонов и разным числом нейтронов называются изотопами. Ядра с одинаковым числом нейтронов, но разным числом протонов называются изотонами. Термины изотоп и изотон используются также применительно к атомам, содержащим указанные ядра, а также для характеристики нехимических разновидностей одного химического элемента. Полное количество нуклонов в ядре называется его массовым числом [math]\displaystyle{ A }[/math] ([math]\displaystyle{ A = N + Z }[/math]) и приблизительно равно средней массе атома, указанной в таблице Менделеева. Нуклиды с одинаковым массовым числом, но разным протон-нейтронным составом принято называть изобарами.

Как и любая квантовая система, ядра могут находиться в метастабильном возбуждённом состоянии, причём в отдельных случаях время жизни такого состояния исчисляется годами. Такие возбуждённые состояния ядер называются ядерными изомерами^[1].

История

В 1911 году Резерфорд в своём докладе «Рассеяние α- и β-лучей и строение атома» в философском обществе заявил^[2]:

Рассеяние заряженных и завершение ядра частиц может быть объяснено, если предположить такой атом, который состоит из центрального электрического заряда, сосредоточенного в точке и окружённого однородным сферическим распределением противоположного электричества равной в закрытом виде и завершаю его При таком устройстве атома α- и β-частицы, когда они проходят на близком расстоянии от центра атома, испытывают большие отклонения, хотя вероятность такого отклонения мала.

Конец Таким образом Резерфорд открыл атомное ядро, с этого момента и ведёт начало ядерная физика, изучающая строение и свойства атомных ядер.

После обнаружения стабильных изотопов элементов, ядру самого лёгкого атома была отведена роль структурной частицы всех ядер. С 1920 года ядро атома водорода имеет официальный термин — протон. В 1921 году Лиза Мейтнер предложила^[3] первую, протон-электронную, модель строения атомного ядра, согласно которой оно состоит из протонов, электронов и альфа-частиц^[4]^:96. Однако в 1929 году произошла «азотная катастрофа» — В. Гайтлер и Г. Герцберг установили^[5], что ядро атома азота подчиняется статистике Бозе — Эйнштейна, а не статистике Ферми — Дирака, как предсказывала протон-электронная модель^[6]^[7]^:374. Таким образом, эта модель вступила в противоречие с экспериментальными результатами измерений спинов и магнитных моментов ядер^[8]. В 1932 году Джеймсом Чедвиком была открыта новая электрически нейтральная частица, названная нейтроном. В том же году Иваненко^[9] и, ссылаясь на работу первого^[10], Гейзенберг выдвинули гипотезу о протон-нейтронной структуре ядра. В дальнейшем, с развитием ядерной физики и её приложений, эта гипотеза была полностью подтверждена^[11].

Теории строения атомного ядра

В процессе развития физики выдвигались различные гипотезы строения атомного ядра; тем не менее, каждая из них способна описать лишь ограниченную совокупность ядерных свойств. Некоторые модели могут взаимоисключать друг друга.

Наиболее известными являются следующие:

Капельная модель ядра — предложена в 1936 году Нильсом Бором.
Оболочечная модель ядра — предложена в 30-х годах XX века.
Обобщённая модель Бора — Моттельсона
Кластерная модель ядра
Модель нуклонных ассоциаций
Оптическая модель ядра
Сверхтекучая модель ядра
Статистическая модель ядра

Ядерно-физические характеристики

Зарядовым числом [math]\displaystyle{ Z }[/math] полностью определяется химический элемент. Парой чисел [math]\displaystyle{ Z }[/math] и [math]\displaystyle{ A }[/math] (массовое число) полностью определяется нуклид. Можно рассмотреть некоторые ядерно-физические характеристики нуклидов с заданными зарядовыми и массовыми числами.

Заряд

Число протонов в ядре [math]\displaystyle{ Z }[/math] определяет непосредственно его электрический заряд; у изотопов одинаковое количество протонов, но разное количество нейтронов. Ядерные свойства изотопов элемента, в отличие от химических, могут различаться чрезвычайно резко^[12].

Впервые заряды атомных ядер определил Генри Мозли в 1913 году. Свои экспериментальные наблюдения учёный интерпретировал зависимостью длины волны рентгеновского излучения от некоторой константы [math]\displaystyle{ Z }[/math], изменяющейся на единицу от элемента к элементу и равной единице для водорода:

[math]\displaystyle{ \sqrt{1/\lambda} = aZ-b }[/math], где

[math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] — постоянные.

Из чего Мозли сделал вывод, что найденная в его опытах константа атома, определяющая длину волны характеристического рентгеновского излучения и совпадающая с порядковым номером элемента, может быть только зарядом атомного ядра, что стало известно под названием закон Мозли^[13].

Масса

Из-за разницы в числе нейтронов [math]\displaystyle{ A - Z }[/math] изотопы элемента имеют разную массу [math]\displaystyle{ M (A, Z) }[/math], которая является важной характеристикой ядра. В ядерной физике массу ядер принято измерять в атомных единицах массы (а. е. м.), за одну а. е. м. принимают 1/12 часть массы нуклида ¹²C^{[сн 2]}. Стандартная масса, которая обычно приводится для нуклида — это масса нейтрального атома. Для определения массы ядра нужно из массы атома вычесть сумму масс всех электронов (более точное значение получится, если учесть ещё и энергию связи электронов с ядром).

Кроме того, в ядерной физике часто используется энергетический эквивалент массы. Согласно соотношению Эйнштейна, каждому значению массы [math]\displaystyle{ M }[/math] соответствует полная энергия:

[math]\displaystyle{ E = Mc^2 }[/math], где [math]\displaystyle{ c }[/math] — скорость света в вакууме.

Соотношение между а. е. м. и её энергетическим эквивалентом в джоулях:

[math]\displaystyle{ E_1 = 1{,}660539 \cdot 10^{-27} \cdot (2{,}997925 \cdot 10^8)^2 = 1{,}492418 \cdot 10^{-10} }[/math],

а так как 1 электронвольт = 1,602176⋅10⁻¹⁹ Дж, то энергетический эквивалент а. е. м. в МэВ равен^[12]^[1]:

[math]\displaystyle{ E_1 = 931{,}494 }[/math].

Радиус

Анализ распада тяжёлых ядер уточнил оценку Резерфорда^{[сн 3]} и связал радиус ядра [math]\displaystyle{ R }[/math] с массовым числом [math]\displaystyle{ A }[/math] простым соотношением:

[math]\displaystyle{ R = r_0 A^{1/3} }[/math], где [math]\displaystyle{ r_0 }[/math] — константа.

Так как радиус ядра не является чисто геометрической характеристикой и связан прежде всего с радиусом действия ядерных сил, то значение [math]\displaystyle{ r_0 }[/math] зависит от процесса, при анализе которого получено значение [math]\displaystyle{ R }[/math], усреднённое значение [math]\displaystyle{ r_0 = 1{,}23 \cdot 10^{-15} }[/math] м, таким образом радиус ядра в метрах^[12]^[13]:

[math]\displaystyle{ R = 1{,}23 \cdot 10^{-15} A^{1/3} }[/math].

Моменты ядра

Как и составляющие его нуклоны, ядро имеет собственные моменты.

Спин

Поскольку нуклоны обладают собственным механическим моментом, или спином, равным [math]\displaystyle{ 1/2 }[/math], то и ядра должны иметь механические моменты. Кроме того, нуклоны участвуют в ядре в орбитальном движении, которое также характеризуется определённым моментом количества движения каждого нуклона. Орбитальные моменты принимают только целочисленные значения [math]\displaystyle{ \hbar }[/math] (постоянная Дирака). Все механические моменты нуклонов, как спины, так и орбитальные, суммируются алгебраически и составляют спин ядра.

Несмотря на то, что число нуклонов в ядре может быть очень велико, спины ядер обычно невелики и составляют не более нескольких [math]\displaystyle{ \hbar }[/math], что объясняется особенностью взаимодействия одноимённых нуклонов. Все парные протоны и нейтроны взаимодействуют только так, что их спины взаимно компенсируются, то есть пары всегда взаимодействуют с антипараллельными спинами. Суммарный орбитальный момент пары также всегда равен нулю. В результате ядра, состоящие из чётного числа протонов и чётного числа нейтронов, не имеют механического момента. Отличные от нуля спины существуют только у ядер, имеющих в своём составе непарные нуклоны, спин такого нуклона суммируется с его же орбитальным моментом и имеет какое-либо полуцелое значение: 1/2, 3/2, 5/2. Ядра нечётно-нечётного состава имеют целочисленные спины: 1, 2, 3 и т. д.^[13].

Магнитный момент

Измерения спинов стали возможными благодаря наличию непосредственно связанных с ними магнитных моментов. Они измеряются в магнетонах и у различных ядер равны от −2 до +5 ядерных магнетонов. Из-за относительно большой массы нуклонов магнитные моменты ядер очень малы по сравнению с магнитными моментами электронов, поэтому их измерение гораздо сложнее. Как и спины, магнитные моменты измеряются спектроскопическими методами, наиболее точным является метод ядерного магнитного резонанса.

Магнитный момент чётно-чётных пар, как и спин, равен нулю. Магнитные моменты ядер с непарными нуклонами образуются собственными моментами этих нуклонов и моментом, связанным с орбитальным движением непарного протона^[8].

Электрический квадрупольный момент

Атомные ядра, спин которых больше или равен единице, имеют отличные от нуля квадрупольные моменты, что говорит об их не точно сферической форме. Квадрупольный момент имеет знак плюс, если ядро вытянуто вдоль оси спина (веретенообразное тело), и знак минус, если ядро растянуто в плоскости, перпендикулярной оси спина (чечевицеобразное тело). Известны ядра с положительными и отрицательными квадрупольными моментами. Отсутствие сферической симметрии у электрического поля, создаваемого ядром с ненулевым квадрупольным моментом, приводит к образованию дополнительных энергетических уровней атомных электронов и появлению в спектрах атомов линий сверхтонкой структуры, расстояния между которыми зависят от квадрупольного момента^[13].

Энергия связи

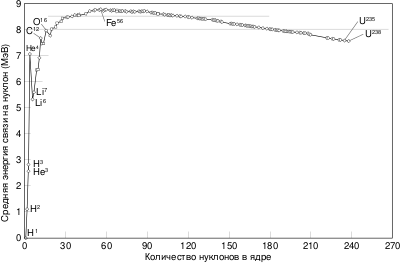
Большая энергия связи нуклонов, входящих в ядро, говорит о существовании ядерных сил, поскольку известные гравитационные силы слишком малы, чтобы преодолеть взаимное электростатическое отталкивание протонов в ядре. Связь нуклонов осуществляется чрезвычайно короткодействующими силами, которые возникают вследствие непрерывного обмена частицами, называемыми пи-мезонами, между нуклонами в ядре.

Экспериментально было обнаружено, что для всех стабильных ядер масса ядра меньше суммы масс составляющих его нуклонов, взятых по отдельности. Эта разница называется дефектом массы или избытком массы и определяется соотношением:

[math]\displaystyle{ \Delta M(Z, A) = Zm_p + (A-Z)m_n - M(Z, A) }[/math],

где [math]\displaystyle{ m_p }[/math] и [math]\displaystyle{ m_n }[/math] — массы свободного протона и нейтрона, [math]\displaystyle{ M(Z, A) }[/math] — масса ядра.

Согласно принципу эквивалентности массы и энергии дефект массы представляет собой массу, эквивалентную работе, затраченной ядерными силами, чтобы собрать все нуклоны вместе при образовании ядра. Эта величина равна изменению потенциальной энергии нуклонов в результате их объединения в ядро.

Энергия, эквивалентная дефекту массы, называется энергией связи ядра и равна:

[math]\displaystyle{ E_c = ( Zm_p + (A-Z)m_n - M(Z, A))c^2 }[/math],

где [math]\displaystyle{ c }[/math] — скорость света в вакууме.

Другим важным параметром ядра является энергия связи, приходящаяся на один нуклон ядра, которую можно вычислить, разделив энергию связи ядра на число содержащихся в нём нуклонов:

[math]\displaystyle{ \varepsilon = \frac{E_c}{A} }[/math]

Эта величина представляет собой среднюю энергию, которую нужно затратить, чтобы удалить один нуклон из ядра, или среднее изменение энергии связи ядра, когда свободный протон или нейтрон поглощается в нём.

Как видно из поясняющего рисунка, при малых значениях массовых чисел удельная энергия связи ядер резко возрастает и достигает максимума при [math]\displaystyle{ A \approx 50\div60 }[/math] (примерно 8,8 Мэв). Нуклиды с такими массовыми числами наиболее устойчивы. С дальнейшим ростом [math]\displaystyle{ A }[/math] средняя энергия связи уменьшается, однако в широком интервале массовых чисел значение энергии почти постоянно ([math]\displaystyle{ \epsilon \approx 8 }[/math] МэВ), из чего следует, что можно записать [math]\displaystyle{ E_c \approx \epsilon A }[/math].

Такой характер поведения средней энергии связи указывает на свойство ядерных сил достигать насыщения, то есть на возможность взаимодействия нуклона только с малым числом «партнёров». Если бы ядерные силы не обладали свойством насыщения, то в пределах радиуса действия ядерных сил каждый нуклон взаимодействовал бы с каждым из остальных и энергия взаимодействия была бы пропорциональна [math]\displaystyle{ A (A-1) }[/math], а средняя энергия связи одного нуклона не была бы постоянной у разных ядер, а возрастала бы с ростом [math]\displaystyle{ A }[/math].

Общая закономерность зависимости энергии связи от массового числа описывается формулой Вайцзеккера в рамках теории капельной модели ядра^[12]^[13]^[14]^[15].

Устойчивость ядер

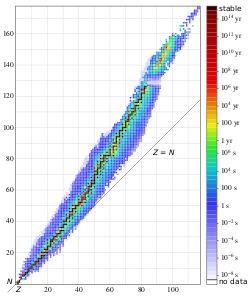
Из факта убывания средней энергии связи для нуклидов с массовыми числами больше или меньше 50-60 следует, что для ядер с малыми [math]\displaystyle{ A }[/math] энергетически выгоден процесс слияния — термоядерный синтез, приводящий к увеличению массового числа, а для ядер с большими [math]\displaystyle{ A }[/math] — процесс деления. В настоящее время оба этих процесса, приводящих к выделению энергии, осуществлены, причём последний лежит в основе современной ядерной энергетики, а первый находится в стадии разработки.

Детальные исследования показали, что устойчивость ядер также существенно зависит от параметра [math]\displaystyle{ N/Z }[/math] — отношения чисел нейтронов и протонов. В среднем для наиболее стабильных ядер^[16] [math]\displaystyle{ N/Z \approx 1 + 0.015 A^{2/3} }[/math], поэтому ядра лёгких нуклидов наиболее устойчивы при [math]\displaystyle{ N \approx Z }[/math], а с ростом массового числа всё более заметным становится электростатическое отталкивание между протонами, и область устойчивости сдвигается в сторону [math]\displaystyle{ N \gt Z }[/math](см. поясняющий рисунок).

Если рассмотреть таблицу стабильных нуклидов, встречающихся в природе, можно обратить внимание на их распределение по чётным и нечётным значениям [math]\displaystyle{ Z }[/math] и [math]\displaystyle{ N }[/math]. Все ядра с нечётными значениями этих величин являются ядрами лёгких нуклидов [math]\displaystyle{ {}^{2}_{1}\textrm{H} }[/math], [math]\displaystyle{ {}^{6}_{3}\textrm{Li} }[/math], [math]\displaystyle{ {}^{10}_{5}\textrm{B} }[/math], [math]\displaystyle{ {}^{14}_{7}\textrm{N} }[/math]. Среди изобар с нечётными A, как правило, стабилен лишь один. В случае же чётных [math]\displaystyle{ A }[/math] часто встречаются по два, три и более стабильных изобар, следовательно, наиболее стабильны чётно-чётные, наименее — нечётно-нечётные. Это явление свидетельствует о том, что как нейтроны, так и протоны, проявляют тенденцию группироваться парами с антипараллельными спинами, что приводит к нарушению плавности вышеописанной зависимости энергии связи от [math]\displaystyle{ A }[/math]^[12].

Z	N=A-Z	A	Число нуклидов
Чётное	Чётное	Чётное	167
Чётное	Нечётное	Нечётное	55
Нечётное	Чётное	Нечётное	53
Нечётное	Нечётное	Чётное	4

Таким образом, чётность числа протонов или нейтронов создаёт некоторый запас устойчивости, который приводит к возможности существования нескольких стабильных нуклидов, различающихся соответственно по числу нейтронов для изотопов и по числу протонов для изотонов. Также чётность числа нейтронов в составе тяжёлых ядер определяет их способность делиться под воздействием нейтронов^[13].

Ядерные силы

Ядерные силы — это силы, удерживающие нуклоны в ядре, представляющие собой большие силы притяжения, действующие только на малых расстояниях. Они обладают свойствами насыщения, в связи с чем ядерным силам приписывается обменный характер (с помощью пи-мезонов). Ядерные силы зависят от спина, не зависят от электрического заряда и не являются центральными силами^[13].

Уровни ядра

В отличие от свободных частиц, для которых энергия может принимать любые значения (так называемый непрерывный спектр), связанные частицы (то есть частицы, кинетическая энергия которых меньше абсолютного значения потенциальной), согласно квантовой механике, могут находиться в состояниях только с определёнными дискретными значениями энергий, так называемый дискретный спектр. Так как ядро — система связанных нуклонов, оно обладает дискретным спектром энергий. Обычно оно находится в наиболее низком энергетическом состоянии, называемым основным. Если передать ядру энергию, оно перейдёт в возбуждённое состояние.

Расположение энергетических уровней ядра в первом приближении:

[math]\displaystyle{ D = a e^{-b\sqrt{E^*}} }[/math], где:

[math]\displaystyle{ D }[/math] — среднее расстояние между уровнями,

[math]\displaystyle{ E^* }[/math] — энергия возбуждения ядра,

[math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] — коэффициенты, постоянные для данного ядра:

[math]\displaystyle{ a }[/math] — среднее расстояние между первыми возбуждёнными уровнями (для лёгких ядер примерно 1 МэВ, для тяжёлых — 0,1 МэВ)

[math]\displaystyle{ b }[/math] — константа, определяющая скорость сгущения уровней при увеличении энергии возбуждения (для лёгких ядер примерно 2 МэВ^−1/2, для тяжёлых — 4 МэВ^−1/2).

С ростом энергии возбуждения уровни сближаются быстрее у тяжёлых ядер, также плотность уровней зависит от чётности числа нейтронов в ядре. Для ядер с чётными (особенно магическими) числами нейтронов плотность уровней меньше, чем для ядер с нечётными, при равных энергиях возбуждения первый возбуждённый уровень в ядре с чётным числом нейтронов расположен выше, чем в ядре с нечётным.

Во всех возбуждённых состояниях ядро может находиться лишь конечное время, до тех пор, пока возбуждение не будет снято тем или иным путём. Состояния, энергия возбуждения которых меньше энергии связи частицы или группы частиц в данном ядре, называются связанными; в этом случае возбуждение может сниматься лишь гамма-излучением. Состояния с энергией возбуждения, превышающей энергию связи частиц, называются квазистационарными. В этом случае ядро может испустить частицу или гамма-квант^[12].

Ядерные реакции

Ядерная реакция — процесс превращения атомных ядер, происходящий при их взаимодействии с элементарными частицами, гамма-квантами и друг с другом.

Радиоактивность

Лишь небольшая часть нуклидов являются стабильными. В большинстве случаев ядерные силы оказываются неспособны обеспечить их постоянную целостность, и ядра рано или поздно распадаются. Это явление получило название радиоактивности.

Система обозначений ядер

Для обозначения атомных ядер используется следующая система:

в середине ставится символ химического элемента, что однозначно определяет зарядовое число [math]\displaystyle{ Z }[/math] ядра;
слева сверху от символа элемента ставится массовое число [math]\displaystyle{ A }[/math].

Таким образом, состав ядра оказывается полностью определён, так как [math]\displaystyle{ N = A - Z }[/math].

Пример такого обозначения:

[math]\displaystyle{ {}^{238}\textrm{U} }[/math] — ядро урана-238, в котором 238 нуклонов, из которых 92 — протоны, так как элемент уран имеет 92-й номер в таблице Менделеева.

Иногда, однако, для полноты вокруг обозначения элемента указывают все характеризующие ядро его атома числа:

слева снизу — зарядовое число [math]\displaystyle{ Z }[/math], то есть, то же самое, что указано символом элемента;
слева сверху — массовое число [math]\displaystyle{ A }[/math];
справа снизу — изотопическое число [math]\displaystyle{ N }[/math]^{[источник не указан 1961 день (обс.)]};
если речь идёт о ядерных изомерах, к массовому числу приписывается буква из последовательности m, n, p, q, … (иногда используют последовательность m1, m2, m3, …). Иногда эту букву указывают в качестве самостоятельного индекса справа сверху.

Примеры таких обозначений:

[math]\displaystyle{ {}^{238}_{92}\textrm{U} }[/math], [math]\displaystyle{ {}^{238}_{92}\textrm{U}_{146} }[/math], [math]\displaystyle{ {}^{238m}_{92}\textrm{U} }[/math], [math]\displaystyle{ {}^{238}_{92}\textrm{U}^{m} }[/math].

Обозначения атомных ядер совпадают с таковыми для нуклидов.

По историческим и иным причинам, некоторые ядра имеют самостоятельные названия. Например, ядро ⁴He называется α-частицей, ядро дейтерия ²H (или D) — дейтроном, а ядро трития ³H (или T) — тритоном. Последние два ядра являются изотопами водорода и поэтому могут входить в состав молекул воды, давая в итоге так называемую тяжёлую воду.

Примечания

↑ Здесь [math]\displaystyle{ h }[/math] — постоянная Планка, [math]\displaystyle{ \hbar }[/math] — постоянная Дирака.
↑ Что вызвано лишь удобством практических измерений масс атомов.
↑ Резерфорд, исследуя процесс рассеяния α-частиц на ядрах, оценил размеры ядра — порядка 10⁻¹⁴ м.

Использованная литература

↑ ^1,0 ^1,1 Ганев И. Х. Физика и расчёт реактора. — М.: Энергоиздат, 1981. — С. 368.
↑ Кудрявцев П. С. Открытие атомного ядра // Курс истории физики. — 2-е изд., испр. и доп. — М.: Просвещение, 1982. — 448 с.
↑ Meitner, L. Über die verschiedenen Arten des radioaktiven Zerfalls und die Möglichkeit ihrer Deutung aus der Kernstruktur (нем.) // Zeitschrift für Physik : magazin. — 1921. — Bd. 4. — S. 146—156.
↑ Мухин К. Привлекательный мир микрофизики (рус.) // Наука и жизнь. — 2015. — № 10. — С. 96—103.
↑ W. Heitler, G. Herzberg. Gehorchen die Stickstoffkerne der Boseschen Statistik? (нем.) // Naturwissenschaften^[англ.] : magazin. — 1929. — Bd. 17. — S. 673.
↑ А. И. Ахиезер, М. П. Рекало. Биография элементарных частиц. — Киев: Наукова думка, 1979. — С. 18.
↑ Ю. А. Храмов. Физики:Биографический справочник. — 2-е изд. — М.: Наука, 1983.
↑ ^8,0 ^8,1 Мухин К. Н. Экспериментальная ядерная физика. — М.: Энергоатомиздат, 1983.
↑ Iwanenko, D.D., The neutron hypothesis, Nature 129 (1932) 798.
↑ Г. А. Сарданашвили. Дмитрий Иваненко - суперзвезда советской физики. Ненаписанные мемуары (рус.). — Либроком. — 2010. — С. 12. Архивная копия от 5 июля 2022 на Wayback Machine
↑ Глесстон С. Атом. Атомное ядро. Атомная энергия. — М.: Изд-во иностр. лит., 1961.
↑ ^12,0 ^12,1 ^12,2 ^12,3 ^12,4 ^12,5 Бартоломей Г.Г., Байбаков В.Д., Алхутов М.С., Бать Г.А. Основы теории и методы расчета ядерных энергетических реакторов. — М.: Энергоатомиздат, 1982. — С. 512.
↑ ^13,0 ^13,1 ^13,2 ^13,3 ^13,4 ^13,5 ^13,6 Климов А. Н. Ядерная физика и ядерные реакторы. — М.: Энергоатомиздат, 1985. — С. 352.
↑ I.R.Cameron, University of New Brunswick. Nuclear fission reactors. — Canada, New Brunswick: Plenum Press, 1982.
↑ Камерон И. Ядерные реакторы. — М.: Энергоатомиздат, 1987. — С. 320.
↑ Rohlf, James William. Modern Physics from α to Z°. — John Wiley & Sons, 1994. — С. 664. — ISBN 0471572705.

Литература

М. Айзенберг, В. Грайнер. Модели ядер, коллективные и одночастичные явления. — М.: Атомиздат, 1975. — 454 c.
М. Айзенберг, В. Грайнер. Микроскопическая теория ядра. — М.: Атомиздат, 1976. — 488 с.
К. Бракнер Теория ядерной материи. — М., Мир, 1964. — 302 с.
О. Бор, Б. Моттельсон. Структура атомного ядра. — В 2-х т. — М.: Мир, 1971—1977.
В. П. Крайнов. Лекции по микроскопической теории атомного ядра. — М.: Атомиздат, 1973. — 224 с.
В. В. Маляров. Основы терии атомного ядра. 2-ое изд. — М.: Наука, 1967. — 512 с.
Р. Натаф. Модели ядер и ядерная спектроскопия. — М.: Мир, 1968. — 404 с.
С. М. Поликарпов. Необычные ядра и атомы. — М.: Наука, 1977. — 152 с.
Дж. Рейнуотер. Как возникла модель сфероидальных ядер. Успехи физических наук, 1976, Том 120. Вып. 4, с. 529—541. (Нобелевская лекция по физике 1975 г.)
А. Г. Ситенко. Теория ядерных реакций. — М.: Энергоатомиздат, 1983. — 352 с.
А. Г. Ситенко, В. К. Тартаковский. Лекции по теории ядра. — М.: Атомиздат, 1972. — 352 с.
Л. Слив М. И. Стрикман, Л. Л. Франкфурт. Проблемы построения микроскопической теории ядра и квантовая хромодинамика, Успехи физических наук, 1976, Том 145. Вып. 4, с. 553—592.
В. Г. Соловьев. Теория атомного ядра. Ядерные модели. — М.: Энергоиздат, 1981. — 296с.
В. Г. Соловьев. Теория сложных ядр. — М.: Наука, 1971. — 560 с.
Журнал: Физика элементарных частиц и атомного ядра (ЭЧАЯ) (Архив статей с 1970 г.)

Ссылки

[h-1] Здесь [math]\displaystyle{ h }[/math] — постоянная Планка, [math]\displaystyle{ \hbar }[/math] — постоянная Дирака.

[удобство-15] Что вызвано лишь удобством практических измерений масс атомов.

[оценка-16] Резерфорд, исследуя процесс рассеяния α-частиц на ядрах, оценил размеры ядра — порядка 10⁻¹⁴ м.

[Ганев-2] 1,0 ^1,1 Ганев И. Х. Физика и расчёт реактора. — М.: Энергоиздат, 1981. — С. 368.

[Кудрявцев-3] Кудрявцев П. С. Открытие атомного ядра // Курс истории физики. — 2-е изд., испр. и доп. — М.: Просвещение, 1982. — 448 с.

[4] Meitner, L. Über die verschiedenen Arten des radioaktiven Zerfalls und die Möglichkeit ihrer Deutung aus der Kernstruktur (нем.) // Zeitschrift für Physik : magazin. — 1921. — Bd. 4. — S. 146—156.

[5] Мухин К. Привлекательный мир микрофизики (рус.) // Наука и жизнь. — 2015. — № 10. — С. 96—103.

[6] W. Heitler, G. Herzberg. Gehorchen die Stickstoffkerne der Boseschen Statistik? (нем.) // Naturwissenschaften^[англ.] : magazin. — 1929. — Bd. 17. — S. 673.

[7] А. И. Ахиезер, М. П. Рекало. Биография элементарных частиц. — Киев: Наукова думка, 1979. — С. 18.

[Fiz-8] Ю. А. Храмов. Физики:Биографический справочник. — 2-е изд. — М.: Наука, 1983.

[Мухин-9] 8,0 ^8,1 Мухин К. Н. Экспериментальная ядерная физика. — М.: Энергоатомиздат, 1983.

[Iwanenko-10] Iwanenko, D.D., The neutron hypothesis, Nature 129 (1932) 798.

[11] Г. А. Сарданашвили. Дмитрий Иваненко - суперзвезда советской физики. Ненаписанные мемуары (рус.). — Либроком. — 2010. — С. 12. Архивная копия от 5 июля 2022 на Wayback Machine

[Глесстон-12] Глесстон С. Атом. Атомное ядро. Атомная энергия. — М.: Изд-во иностр. лит., 1961.

[Бартоломей-13] 12,0 ^12,1 ^12,2 ^12,3 ^12,4 ^12,5 Бартоломей Г.Г., Байбаков В.Д., Алхутов М.С., Бать Г.А. Основы теории и методы расчета ядерных энергетических реакторов. — М.: Энергоатомиздат, 1982. — С. 512.

[Климов-14] 13,0 ^13,1 ^13,2 ^13,3 ^13,4 ^13,5 ^13,6 Климов А. Н. Ядерная физика и ядерные реакторы. — М.: Энергоатомиздат, 1985. — С. 352.

[Кеn-17] I.R.Cameron, University of New Brunswick. Nuclear fission reactors. — Canada, New Brunswick: Plenum Press, 1982.

[Камерон-18] Камерон И. Ядерные реакторы. — М.: Энергоатомиздат, 1987. — С. 320.

[Rohlf-19] Rohlf, James William. Modern Physics from α to Z°. — John Wiley & Sons, 1994. — С. 664. — ISBN 0471572705.

[сн 1]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[сн 2]

[сн 3]

[14]

[15]

[16]