Тор (поверхность)

Красным — образующая окружность

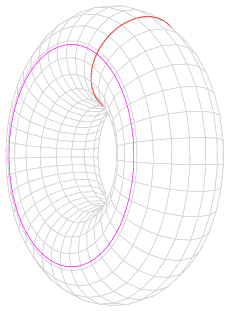
Тор (тороид) — поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей её.

Обобщенно, тор — топологическое пространство или гладкое многообразие, эквивалентное такой поверхности.

Иногда не требуют, чтобы ось вращения не пересекала образующую окружность. В таком случае, если ось вращения пересекает образующую окружность (или касается её), то тор называют закрытым, иначе открытым.

Понятие тора определяется и в многомерном случае. Тор является примером коммутативной алгебраической группы и примером группы Ли.

История

Тороидальная поверхность впервые была рассмотрена древнегреческим математиком Архитом при решении задачи об удвоении куба. Другой древнегреческий математик, Персей, написал книгу о спирических линиях — сечениях тора плоскостью, параллельной его оси.

Ось тора

Ось вращения может пересекать окружность, касаться её и располагаться вне окружности. В первых двух случаях тор называется закрытым, в последнем — открытым, или кольцом.

• Изменение расстояния до оси вращения
• 
• 
• 
• 
• 
• 

Окружность, состоящая из центров образующих окружностей, называется направляющей окружностью.

Топологические свойства

Тор является поверхностью рода 1 (сфера с одной ручкой). Тор является компактным топологическим пространством.

Тор имеет характеристику Эйлера — Пуанкаре χ=0.

Уравнения

Параметрическое

Уравнение тора с расстоянием от центра образующей окружности до оси вращения R и с радиусом образующей окружности r может быть задано параметрически в виде:

[math]\displaystyle{ \left\{ \begin{matrix} x(\varphi,\psi) = & (R + r \cos \psi) \cos \varphi \\ y(\varphi,\psi) = & (R + r \cos \psi) \sin \varphi \\ z(\varphi,\psi) = & r \sin \psi \\ \end{matrix} \right. \qquad \varphi \in [0,2\pi), \psi \in [-\pi,\pi) }[/math]

Алгебраическое

Непараметрическое уравнение в тех же координатах и с теми же радиусами имеет четвёртую степень:

[math]\displaystyle{ \left( x^2+y^2+z^2+R^2-r^2 \right)^2-4R^2\left(x^2+y^2\right)=0 }[/math]

Такая поверхность имеет четвёртый порядок.

Существуют другие поверхности, диффеоморфные тору, имеющие другой порядок.

[math]\displaystyle{ y^2=x^3+x+1 }[/math], где x, y комплексные числа. Комплексная эллиптическая кривая, кубическая поверхность.

[math]\displaystyle{ \left\{ \begin{matrix} x^2+y^2 = 1 \\ z^2+t^2 = 1 \\ \end{matrix} \right. }[/math] Вложение тора в 4-мерное пространство. Это поверхность 2 порядка. Кривизна этой поверхности равна 0.

Кривизна поверхности

На торе есть точки с положительной, нулевой и отрицательной гауссовой кривизной.

Тор в трёхмерном пространстве имеет точки положительной и отрицательной кривизны. В соответствии с теоремой Гаусса-Бонне интеграл кривизны по всей поверхности тора равен нулю.

Свойства

Этапы выворачивания тора

Вариант окраски участков тора

• Площадь поверхности тора как следствие из первой теоремы Гюльдена: [math]\displaystyle{ S=4\pi^2 R r }[/math].
• Объём тела, ограничиваемого тором (полнотория), как следствие из второй теоремы Паппа — Гюльдена: [math]\displaystyle{ V=2\pi^2 R r^2 }[/math].
• Тор с вырезанным диском («проколотый») можно вывернуть наизнанку непрерывным образом (топологически, то есть серией диффеоморфизмов). При этом две пересекающиеся перпендикулярно окружности на нём («параллель» и «меридиан») поменяются местами.
• Два таких «дырявых» тора, сцепленных между собой, можно продеформировать так, чтобы один из торов «проглотил» другой.
• Минимальное число цветов, необходимое для раскрашивания участков тора так, чтобы соседние были разного цвета, равно 7. См. также Проблема четырёх красок.

Сечения

Анимация, показывающая разрезание тора бикасательной плоскостью и две получающиеся окружности Вилларсо

Сечения

• При сечении тора бикасательной плоскостью получающаяся кривая четвёртого порядка оказывается вырожденной: пересечение является объединением двух окружностей называемых окружностями Вилларсо.
  • В частности, открытый тор может быть представлен как поверхность вращения окружности зацепленной за ось вращения
• Одно из сечений открытого тора — лемниската Бернулли, другие кривые линии являются графическими линиями и называются кривыми Персея (спирическими линиями, сечениями тора плоскостью, параллельной его оси)
• Некоторые пересечения поверхности тора плоскостью внешне напоминают эллипс (кривую 2-го порядка). Получаемая таким образом кривая выражается алгебраическим уравнением 4-го порядка.

Обобщения

Многомерный тор

Стереографическая проекция

Обобщением 2-мерного тора является многомерный тор (также n-тор или гипертор):

[math]\displaystyle{ \mathbf{T}^n = \underbrace{S^1 \times \cdots \times S^1}_n. }[/math]

Поверхность вращения

Тор — частный случай поверхности вращения.

См. также

• Полноторие
• Цилиндрические и тороидальные шахматы

Литература

• Савёлов А. А. Плоские кривые: Систематика, свойства, применения. М.: Физматгиз, 1960. 293 с. Переиздана в 2002 году, ISBN 5-93972-125-7