Полноторие

Полното́рие (полното́рий) — трёхмерная фигура, ограниченная тором, а также топологическое пространство, гомеоморфное этой фигуре, то есть прямое произведение [math]\displaystyle{ D^2 \times S^1 }[/math]двумерного диска и окружности. Неформально, полноторие — бублик, тогда как тор — только его поверхность (пустотелая камера колеса).

Свойства

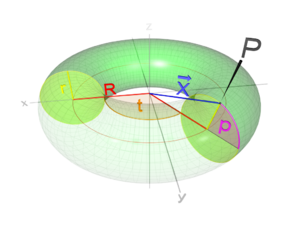
Полноторие может быть получено как фигура вращения круга радиуса [math]\displaystyle{ r }[/math] вокруг оси, лежащей в плоскости этого круга, находящийся на расстоянии [math]\displaystyle{ R }[/math] от его центра.
Объём полнотория как следствие из второй теоремы Гульдина: [math]\displaystyle{ V=2\pi^2 R r^2 }[/math], где [math]\displaystyle{ r }[/math] — радиус образующего круга, а [math]\displaystyle{ R }[/math] — расстояние от центра образующего круга до оси вращения (см. рисунок).
Полноторие является трёхмерным компактным многообразием с краем. Это многообразие является связным и ориентируемым.
Полноторие гомотопически эквивалентно окружности [math]\displaystyle{ S^1 }[/math]. Отсюда следует, что полноторие и окружность имеют одинаковые фундаментальные группы и группы гомологий:

[math]\displaystyle{ \pi_1(S^1 \times D^2) \cong \pi_1(S^1) \cong \mathbb{Z} }[/math]

[math]\displaystyle{ H_k(S^1 \times D^2) \cong H_k(S^1) \cong \begin{cases} \mathbb{Z} & k = 0,1 \\ 0 & k\ge 2 \end{cases} }[/math]

Литература

Фоменко А. Т. Наглядная геометрия и топология — М., 1992.
Фоменко А. Т., Фукс Д. Б. Курс гомотопической топологии.— М.: Наука, 1989.