Математический софизм

Плакат Якова Гуминера «Арифметика встречного промфинплана» (1931 год)

Математический софизм (от греч. σόφισμα — уловка, хитрая выдумка, головоломка) — ошибочное математическое утверждение, полученное с помощью рассуждений, которые кажутся правильными, но в действительности содержат ту или иную ошибку. Причины ошибки могут быть разнообразными — применение запрещённых в математике действий (например, деление на ноль), неточное использование математических законов или использование вне зоны их применимости, логические ошибки и т. д.

Математический софизм является частным случаем софизма. Далее в данной статье речь идёт только о математических софизмах, которые для краткости будут называться просто софизмами. Не следует путать софизмы с научными парадоксами (например, с апориями Зенона, парадоксом дней рождения или парадоксом Банаха — Тарского), которые не содержат ошибок и часто обладают немалой научной ценностью.

Разбор софизмов, поиск ошибок в них исключительно ценны в ходе преподавания математики, они помогают учащимся и студентам сформировать ясное понимание математических и логических законов, а также предостерегают от возможных типичных ошибок в применении этих законов.

История

Прокл Диадох (V век н. э.) в своих комментариях к «Началам» Евклида сообщил, что ещё Евклид в III веке до н. э. составил сборник математических софизмов в помощь изучающим геометрию; сборник назывался «Псевдария» и до наших дней не дошёл. Цель софизмов, согласно Проклу — научить учащихся обнаруживать ошибки в рассуждениях и избегать их в дальнейшем.

В дальнейшем, вплоть до наших дней, учебная литература, а также сборники по занимательной математике, часто включают софизмы с заданием «найдите ошибку», на основе которых поясняются математические правила и проверяются знания читателей.

Классификация софизмов

Существует несколько вариантов группировки софизмов — одни авторы группируют их по виду математической тематики, другие по типу ошибки в рассуждениях, третьи сочетают в том или ином виде оба подхода.

Российский педагог В. И. Обреимов предложил делить софизмы по типу ошибочного результата:

1. Равенство неравных.
2. Неравенство равных.
3. Меньшее превышает большее.
4. Геометрические несообразности.
5. Мнимое реально (ошибки в рассуждениях о комплексных числах).
6. Неразрешимые уравнения.

Эта классификация подверглась критике за то, что материал по одной и той же ошибке сводит вместе разные разделы математики, что методологически неправильно, и к тому же классификационные признаки недостаточно существенны.

Немецкий математик Герман Шуберт рассматривал четыре типа софизмов («Математические развлечения и игры», 1897):

1. Деление на ноль.
2. Двузначность квадратного корня.
3. Ошибки в геометрических построениях.
4. Некорректная работа с бесконечностью.

Книга В. М. Брадиса и других отмечает очевидную неполноту этого списка и предлагает свою:

1. Неправильности речи.
2. Распространение на исключительные случаи (например, деление на ноль).
3. Приписывание свойств определённого вида всему роду. Например, обе части неравенства можно сократить на общий положительный множитель, но если множитель отрицательный, важно не забыть изменить знак неравенства на противоположный.
4. Неправильное применение принципа непосредственных умозаключений путём обращения. Например, из равенства чисел следует равенство их квадратов, но обратное неверно.
5. Подмена точных определений геометрической интуицией.
6. Ошибки построения,
7. Ошибки, являющиеся следствием буквального толкования сокращённой (условной) формулировки некоторых геометрических утверждений.
8. Нарушение смысла условных записей.
9. Уклонение от тезиса, то есть доказательство не того утверждения, которое первоначально сформулировано.

Сам материал софизмов в книге Брадиса и др. изложен строго по темам: арифметика, алгебра, геометрия, тригонометрия, приближённые вычисления. Данная статья также придерживается тематического разбиения материала как наиболее удобного для преподавателей и учащихся.

Элементарная математика

Алгебра

Деление на ноль

Софизм. Пусть [math]\displaystyle{ a,b }[/math] — произвольные числа. Обозначим их разность буквой [math]\displaystyle{ c, }[/math] то есть [math]\displaystyle{ a-b=c. }[/math] Умножим это равенство на [math]\displaystyle{ a-b\colon \quad (a-b)^2=c(a-b). }[/math] Раскроем скобки: [math]\displaystyle{ a^2-2ab+b^2=ca-cb. }[/math] Далее сгруппируем одночлены следующим образом: [math]\displaystyle{ a^2-ab-ac=ab-b^2-bc, }[/math] или:

[math]\displaystyle{ a(a-b-c) = b(a-b-c). }[/math]

Сократив на [math]\displaystyle{ a-b-c, }[/math] получаем: [math]\displaystyle{ a=b, }[/math] то есть все числа равны.

• Причина ошибки: поскольку [math]\displaystyle{ a-b=c, }[/math] мы не имеем права сокращать на [math]\displaystyle{ a-b-c, }[/math] потому что это выражение равно нулю, а сокращать (то есть делить) на ноль нельзя.

Деление на ноль — одна из самых частых алгебраических ошибок, причём это деление может быть замаскировано, например, под сокращение общего множителя. Например, сокращая уравнение [math]\displaystyle{ 9x^2=x }[/math] на [math]\displaystyle{ x, }[/math] мы теряем корень [math]\displaystyle{ x=0. }[/math] Другой софизм — уравнение:

[math]\displaystyle{ \sqrt{x-5}\cdot x = 4\sqrt{x-5}. }[/math]

Сокращая на [math]\displaystyle{ \sqrt{x-5}, }[/math] мы не только теряем единственный корень уравнения [math]\displaystyle{ x=5, }[/math] но попутно приобретаем лишний корень [math]\displaystyle{ x=4, }[/math] который не входит в область допустимых значений неизвестного, поскольку подкоренное выражение при [math]\displaystyle{ x=4 }[/math] становится отрицательно.

Неравенства

Софизм 1. Пусть [math]\displaystyle{ a, b }[/math] — произвольные положительные числа, причём [math]\displaystyle{ a\gt b. }[/math] Умножив это неравенство на [math]\displaystyle{ b }[/math] и отняв от обеих его частей [math]\displaystyle{ a^2, }[/math] получим: [math]\displaystyle{ ab-a^2\gt b^2-a^2. }[/math] Разложим на множители:

[math]\displaystyle{ a(b-a) \gt (b+a)(b-a) }[/math]

Сократив на [math]\displaystyle{ b-a }[/math] (по условию оно не равно нулю), получим неравенство: [math]\displaystyle{ a\gt b+a. }[/math] Отнимем от обеих частей [math]\displaystyle{ a, }[/math] результат: [math]\displaystyle{ 0\gt b. }[/math] То есть любое положительное число [math]\displaystyle{ b }[/math] одновременно и отрицательное.

• Причина ошибки: обе части неравенства можно сокращать на общий ненулевой множитель, но если этот множитель отрицательный, то знак неравенства должен быть изменён на противоположный. Здесь именно тот случай, так как [math]\displaystyle{ b-a\lt 0. }[/math] После сокращение получим: [math]\displaystyle{ a\lt b+a, }[/math] ошибка устранена.

Извлечение корня

Софизм 1. Верное равенство: [math]\displaystyle{ 1-3+\frac94 = 4-6+\frac94 }[/math] можно записать в виде: [math]\displaystyle{ \left(1-\frac32\right)^2 = \left(2-\frac32\right)^2. }[/math] Извлекая квадратный корень, получаем: [math]\displaystyle{ 1-\frac32=2-\frac32, }[/math] откуда: [math]\displaystyle{ 1=2. }[/math]

• Причина ошибки: из равенства квадратов величин следует равенство самих величин только если они имеют одинаковые знаки. Правильное извлечение корня даёт результат с абсолютной величиной: [math]\displaystyle{ \left|1-\frac32\right|=\left|2-\frac32\right|, }[/math] и тогда ошибка не возникает.

Софизм 2. В старших классах определяется возведение числа не только в целую, но и в дробную степень: [math]\displaystyle{ a^{m/n} = (\sqrt[n]{a})^m. }[/math] Рассмотрим софизм, доказывающий, что [math]\displaystyle{ -1 = 1 }[/math].

[math]\displaystyle{ -1 = (-1)^{\frac{2}{2}} = (-1)^{2\ \cdot\ \frac{1}{2}} = \left({(-1)^2}\right)^\frac{1}{2}=1^\frac{1}{2}={\color{blue}\sqrt{\color{black}1}}= 1 }[/math]

• Причина ошибки: возведение в дробную степень определяется только для неотрицательных чисел.

Софизм 3. Следует проявлять осторожность при возведении в дробную степень значений тригонометрических функций. Кажется очевидным, что [math]\displaystyle{ (\cos^2 x)^{3/2} = \cos^3 x, }[/math] однако при [math]\displaystyle{ x=\pi }[/math] получаем ошибочное равенство: [math]\displaystyle{ 1^{3/2} = -1. }[/math] Выше уже пояснялось, что арифметический корень из квадрата числа равен абсолютной величине числа, так что правильная запись следующая: [math]\displaystyle{ (\cos^2 x)^{3/2} = |\cos x|^3. }[/math]

Некорректные условия задачи

Софизм 1. Решаем уравнение: [math]\displaystyle{ 3\sqrt{x} + x + 2 = 0. }[/math]

[math]\displaystyle{ 3\sqrt{x} = -(x + 2); \quad 9x=x^2+4x+4;\quad x^2-5x+4=0 }[/math]

[math]\displaystyle{ x_1 = 4;\quad x_2 = 1 }[/math]

Проверка: подстановка первого корня в уравнение даёт равенство [math]\displaystyle{ 12=0, }[/math] подстановка второго даёт: [math]\displaystyle{ 6=0. }[/math]

• Причина ошибки: исходное уравнение не имеет решений. Это видно из того, что левая часть строго больше нуля [math]\displaystyle{ (x\geqslant0, }[/math] так как он под корнем). При возведении в квадрат появились два посторонних корня, но проверка их отбраковала.

Софизм 2. Решим уравнение: [math]\displaystyle{ x^2-ax = -\frac13 a^2, }[/math] где [math]\displaystyle{ a }[/math] — произвольное вещественное число.

Умножив обе части уравнения на [math]\displaystyle{ (-3a) }[/math] и затем прибавив к ним [math]\displaystyle{ x^3-a^3, }[/math] мы преобразуем уравнение к виду: [math]\displaystyle{ (x-a)^3 = x^3. }[/math] После извлечения кубического корня получается уравнение [math]\displaystyle{ x-a=x, }[/math] откуда: [math]\displaystyle{ a=0, }[/math] то есть все числа равны нулю.

• Причина ошибки: мы обращались с неизвестным [math]\displaystyle{ x }[/math] как с вещественным числом, однако исходное уравнение, как легко убедиться, не имеет вещественных корней (исключая как раз случай [math]\displaystyle{ a=0 }[/math]), потому что его дискриминант [math]\displaystyle{ D=-a^2/3 \leqslant 0. }[/math] Если же рассматривать уравнение в системе комплексных чисел, то все рассуждения до извлечения кубического корня верны, но комплексный кубический корень имеет три значения, поэтому из равенства кубов не следует равенства самих величин.

Геометрия

См. также: Исчезновение клетки

Исчезновение клетки

Софизм 1. Разрежем треугольник на четыре части, как показано на верхней части рисунка, а затем составим из этих частей новый треугольник такой же величины, как показано на нижней части рисунка. От перестановки местами частей общая площадь изменяется на одну клетку!

• Причина ошибки: прямая, которая кажется гипотенузой треугольника, на деле является ломаной, то есть рассматриваемая фигура — не треугольник, а четырёхугольник. Это легко заключить из того факта, что в красном треугольнике отношение катетов равно 3:8, а в синем — 2:5, что немного больше. Значит, у верхней фигуры ломаная чуть-чуть вогнута, у нижней — чуть-чуть выпукла, и разница в площади как раз даёт «лишнюю» клетку.

Лишняя клетка

У данного софизма имеется множество вариантов, один из которых приведен на рисунке: перекладывая части прямоугольника площадью [math]\displaystyle{ 24\cdot 9 = 216, }[/math] мы получаем прямоугольник площадью [math]\displaystyle{ 31\cdot 7 = 217. }[/math] Причина аналогична: вдоль диагонали второго прямоугольника растянута дырочка площадью в одну клетку.

Софизм о равенстве треугольников

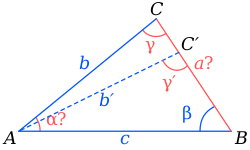
Софизм 2. Будем опираться на признак: два треугольника равны, если у них равны две стороны и один из углов. У треугольников ABC и ABC' равны угол [math]\displaystyle{ \beta }[/math] и две стороны (сторона [math]\displaystyle{ c }[/math] общая, [math]\displaystyle{ b=b' }[/math]) и значит, треугольники равны, что противоречит построению на рисунке (углы [math]\displaystyle{ \gamma }[/math] и [math]\displaystyle{ \gamma' }[/math] не равны 90°, поэтому точки C и C' не совпадают).

• Причина ошибки: небрежная и поэтому ошибочная формулировка признака равенства треугольников, правильно: «два треугольника равны, если у них равны две стороны и угол между ними». Собственно, данный софизм можно рассматривать как убедительное опровержение ошибочного признака.

Софизм о равнобедренности всех треугольников

Софизм 3: «все треугольники равнобедренные» (часто приписывается Льюису Кэрроллу). Рассмотрим произвольный треугольник ABC (см. рисунок). Биссектриса угла A и перпендикуляр к середине стороны BC пересекаются в некоторой точке O. Опустим из точки O перпендикуляры OR (на сторону AB) и OQ (на сторону AC), а также соединим O с вершинами B и C..

Прямоугольные треугольники RAO и QAO равны, потому что у них равны одна сторона (AO) и угол (∠RAO = ∠QAO). Равны также прямоугольные треугольники ROB и QOC, потому что у них равны две стороны: BO = OC и RO = OQ. Но тогда AR = AQ, RB = QC, и сторона AB = AR + RB = AQ + QC = AC — треугольник равнобедренный.

• Причина ошибки: намеренно искажённый чертёж. Если его выполнить аккуратно, точка O будет не внутри, а вне треугольника (на описанной вокруг треугольника окружности). При этом одна из точек R и Q находится на стороне треугольника, а другая — на продолжении другой стороны: если сторона [math]\displaystyle{ AB \gt AC }[/math], то R внутри, Q снаружи, иначе наоборот. В первом случае [math]\displaystyle{ AB = AR + RB; AC = AQ - QC }[/math] — минус вместо плюса; аналогично разбирается второй случай.

Тригонометрия

Стандартные обозначения в треугольнике

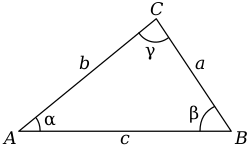
Софизм. Рассмотрим известное тригонометрическое тождество: [math]\displaystyle{ \sin(\pi - \alpha) = \sin \alpha. }[/math] В любом треугольнике сумма углов [math]\displaystyle{ \alpha+\beta+\gamma = \pi, }[/math] поэтому [math]\displaystyle{ \sin(\pi - (\alpha+\beta)) }[/math] равен, с одной стороны, [math]\displaystyle{ \sin (\alpha+\beta) }[/math] по тождеству, а с другой стороны — [math]\displaystyle{ \sin \gamma. }[/math] Следовательно, углы тоже равны: [math]\displaystyle{ \alpha+\beta = \gamma. }[/math] Вычитая это равенство из тождества: [math]\displaystyle{ \alpha+\beta+\gamma = \pi, }[/math] получаем: [math]\displaystyle{ 2 \gamma=\pi, }[/math] или [math]\displaystyle{ \gamma=\pi/2. }[/math] Вывод: любой треугольник — прямоугольный.

• Причина ошибки: равенство [math]\displaystyle{ \sin (\alpha+\beta) = \sin \gamma }[/math] действительно имеет место для любого треугольника, но из него не следует равенство углов — это показывает и формула [math]\displaystyle{ \sin(\pi - \alpha) = \sin \alpha. }[/math] У любых двух углов, дополняющих друг друга до [math]\displaystyle{ \pi, }[/math] синусы одинаковы.

Доказательство по индукции

См. также: Доказательство одноцветности всех лошадей

Софизм. Докажем, что все лошади одной масти. Доказательство ведём индукцией по числу [math]\displaystyle{ N }[/math] лошадей. При [math]\displaystyle{ N=1 }[/math] утверждение тривиально. Пусть все табуны из [math]\displaystyle{ N }[/math] лошадей одной масти; докажем для табуна из [math]\displaystyle{ N+1 }[/math] лошадей. Уберём одну лошадь; все оставшиеся имеют одинаковую масть по предположению индукции. Вернём лошадь в табун и заберём другую лошадь. Тогда и ранее отделявшаяся лошадь получается той же масти.

• Причина ошибки: вторая часть доказательства не работает при переходе от [math]\displaystyle{ N=1 }[/math] к [math]\displaystyle{ N = 2 }[/math] (трюк с отделением лошади тогда ничего не доказывает).

Этот остроумный софизм имеет интересную вариацию: доказательство утверждения, что все целые числа равны. Докажем индукцией по длине [math]\displaystyle{ N }[/math] отрезка натуральных чисел [math]\displaystyle{ 1,2,3,\dots, N }[/math]. При [math]\displaystyle{ N=1 }[/math] чисел в отрезке всего одно, и утверждение справедливо. Пусть утверждение верно для первых [math]\displaystyle{ N }[/math] чисел, докажем для [math]\displaystyle{ N+1. }[/math] Возьмём два произвольных числа [math]\displaystyle{ 1\leqslant a, b\leqslant N+1. }[/math] По предположению индукции [math]\displaystyle{ a-1 = b-1, }[/math] но тогда и [math]\displaystyle{ a=b }[/math] ■ Ошибка здесь аналогична предыдущей: для отрезка длины 2, [math]\displaystyle{ a=1, b=2 }[/math] значение [math]\displaystyle{ a-1 }[/math] выходит за пределы предположения индукции, разрушая логику доказательства.

Высшая математика

Комплексные числа

Софизм 1. Мнимая единица определяется как [math]\displaystyle{ \sqrt{-1}, }[/math] так что [math]\displaystyle{ i^2=-1. }[/math] Но [math]\displaystyle{ i^2=\sqrt{-1}\cdot\sqrt{-1} = \sqrt{(-1)\cdot (-1)} = \sqrt{1} = 1. }[/math] Получается, что [math]\displaystyle{ 1=-1. }[/math]

• Причина ошибки: в системе комплексных чисел надо осторожно обращаться с корнями. Арифметический корень, обозначаемый знаком радикала, определяется только для положительных вещественных чисел, а комплексные квадратные корни из отрицательных чисел двузначны. Поэтому равенство [math]\displaystyle{ \sqrt{1} = 1 }[/math] следует заменить на [math]\displaystyle{ \sqrt{1} = \pm 1, }[/math] и тогда ошибки не возникает.

Софизм 2. Возведём известное тождество [math]\displaystyle{ e^{2\pi i}=1 }[/math] в степень [math]\displaystyle{ i. }[/math] Слева получится [math]\displaystyle{ e^{-2\pi}, }[/math] справа, очевидно, 1. В итоге: [math]\displaystyle{ e^{-2\pi} = 1, }[/math] что, как легко проверить, неверно.

• Причина ошибки: возведение в комплексную степень даёт многозначный результат, поэтому правило [math]\displaystyle{ \left(a^b\right)^c=a^{bc} }[/math] здесь неприменимо, надо использовать общее определение (см. Комплексная степень); Аккуратное применение формул определения комплексной степени даёт слева и справа [math]\displaystyle{ e^{-2\pi k}; }[/math] отсюда видно, что корень ошибки — путаница значений этого выражения при [math]\displaystyle{ k=0 }[/math] и при [math]\displaystyle{ k=1. }[/math]

Пределы функций

Софизм 1. Найдём предел выражения [math]\displaystyle{ \frac{ax+y}{x+ay}, }[/math] когда [math]\displaystyle{ x,y \to \infty. }[/math] Если сначала устремить [math]\displaystyle{ x \to \infty, }[/math] то предел равен [math]\displaystyle{ a }[/math] (независимо от значения [math]\displaystyle{ y }[/math]), а если начать с [math]\displaystyle{ y, }[/math] то предел равен [math]\displaystyle{ 1/a. }[/math] Получается, что любое число равно своему обратному.

• Причина ошибки: собственно, ошибка только в окончательном выводе. Перестановка порядка частичных пределов, вообще говоря, может изменить результат.

Действия с бесконечными рядами

Софизм 1. Рассмотрим бесконечный ряд для натурального логарифма [math]\displaystyle{ \ln 2 }[/math], получаемый из ряда Меркатора при [math]\displaystyle{ x=1\colon }[/math]

[math]\displaystyle{ \ln 2 = 1 - \frac12 + \frac13 - \frac14 + \frac15 - \frac16 \dots }[/math]

Сгруппируем вместе члены с одинаковыми знаками:

[math]\displaystyle{ \ln 2 = \left(1 + \frac13 + \frac15 \dots \right) - \left( \frac12 + \frac14 + \frac16 \dots\right) = \left(1 + \frac13 + \frac15 \dots \right) + \left( \frac12 + \frac14 + \frac16 \dots\right) - 2 \left( \frac12 + \frac14 + \frac16 \dots\right) }[/math]

Объединив первые две скобки и внеся множитель 2 внутрь третьей скобки, получаем разность двух одинаковых величин, то есть ноль, хотя [math]\displaystyle{ \ln 2 }[/math] не равен нулю:

[math]\displaystyle{ \ln 2 = \left(1 + \frac12 + \frac13 + \frac14 \dots \right) - \left( 1 + \frac12 + \frac13 + \frac14 \dots \right) = 0 }[/math]

• Причина ошибки: не всякая перегруппировка членов ряда разрешена, она справедлива только для абсолютно сходящихся рядов. В частности, представление сходящегося исходного ряда в виде разности двух расходящихся рядов некорректно. Ряд [math]\displaystyle{ 1 + \frac12 + \frac13 + \frac14 + \frac15 + \dots }[/math] называется «гармоническим», и он расходится, хотя отличается от исходного только знаками членов.

Интегрирование

Неопределённый интеграл

Софизм. Проинтегрируем два тождества:

[math]\displaystyle{ \frac{d}{dx}\sin^2 x = 2 \sin x \cos x; \quad \frac{d}{dx}\cos^2 x = -2 \sin x \cos x. }[/math]

Результаты:

[math]\displaystyle{ \int{\sin x \cos x dx} = \frac12 \sin^2 x; \quad \int{\sin x \cos x dx} = -\frac12 \cos^2 x }[/math]

Вычитая из первого равенства второе, получаем:

[math]\displaystyle{ \sin^2x+\cos^2 x = 0, }[/math]

в то время как справа должна быть 1.

• Причина ошибки: в значения неопределённых интегралов забыли включить константы интегрирования:

[math]\displaystyle{ \int{\sin x \cos x dx} = \frac12 \sin^2 x + C_1; \quad \int{\sin x \cos x dx} = -\frac12 \cos^2 x + C_2 }[/math]

Определённый интеграл

Софизм 1. Найдём интеграл от положительной функции по формуле Ньютона — Лейбница:

[math]\displaystyle{ \int\limits_{-1}^1 \frac{dx}{x^2} = -\frac{1}{x} \bigg|_{-1}^1 = -1-1 = -2. }[/math]

Интеграл от положительной функции оказался отрицательным («парадокс Даламбера», 1768 год).

• Причина ошибки: подынтегральная функция разрывна (и не ограничена) в нуле, поэтому формула Ньютона — Лейбница к ней неприменима.

Софизм 2. Найдём интеграл от положительной функции методом замены переменной:

[math]\displaystyle{ I = \int\limits_{-1}^1 x^2 dx }[/math]

Введём новую переменную [math]\displaystyle{ y=x^2; dy = x dx }[/math]; отрезок интегрирования [math]\displaystyle{ [-1; 1] }[/math] для [math]\displaystyle{ x }[/math] перейдёт в отрезок [math]\displaystyle{ [1; 1] }[/math] для [math]\displaystyle{ y }[/math]:

[math]\displaystyle{ I = \int\limits_1^1 \sqrt{y} dy = 0. }[/math] Правильный ответ: [math]\displaystyle{ I = \frac23. }[/math]

• Причина ошибки: при замене переменной старая и новая переменные должны находиться во взаимно-однозначном соответствии, иначе обратная функция [math]\displaystyle{ x=x(y) }[/math] не определена; в софизме это правило нарушено.

Другие софизмы

Несколько дополнительных примеров софизмов и парадоксальных выводов, вызвавших оживлённое обсуждение в научном сообществе:

• Задача о двух конвертах в теории вероятностей.
• Парадокс Карри в математической логике.
• Парадокс Скулема в теории множеств.
• Петербургский парадокс

Литература

• Брадис В. М„ Минковский В. Л., Харчева А. К. Ошибки в математических рассуждениях. — 2-е изд. — М.: Учпедгиз, 1959. — 177 с.
  • 3-е издание: М.: Просвещение, 1967. — 191 с.
• Гарднер, Мартин. Геометрические заблуждения (глава 6) // Крестики-нолики. — М.: Мир, 1988. — 325 с. — ISBN 5-03-001234-6.
• Гарднер, Мартин. Математические софизмы (глава 13) // Математические головоломки и развлечения. — М.: Мир, 1971. — 511 с.
• Дворянинов С. В. Преподавание математики и софизмы // Математическое образование. — 2007. — № 1(41).
• Мадера А. Г., Мадера Д. А. Математические софизмы. Правдоподобные рассуждения, приводящие к ошибочным утверждениям / Книга для учащихся 7—11 классов. — М.: Просвещение, 2003. — 112 с. — ISBN 5-09-010795-5.
• Нагибин Ф. Ф., Канин Е. С. Математические софизмы // Математическая шкатулка. Пособие для учащихся. — Издание 4-е. — М.: Просвещение, 1984.
• Обреимов В. И. Математические софизмы. — 2-е изд. — СПб.: Ф. Павленков, 1889. — 79 с.
• Перельман Я. И. Дважды два — пять! (Математические софизмы). — Л.: ДЗН, 1839. — 16 с.
• Фурре, Эмиль. Геометрическiе головоломки и паралогизмы. — Одесса: Mathesis, 1912. — 52 с.
• Bunch, Bryan. Mathematical Fallacies and Paradoxes. — Dover Publications, 1997. — 240 p. — (Dover Books on Mathematics). — ISBN 978-0486296647.

Ссылки

• Classic Fallacies (англ.). Дата обращения: 28 марта 2020.