Майорановский фермион

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
(перенаправлено с «Майорановская частица»)
Майорановский фермион
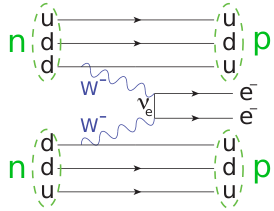Диаграмма Фейнмана двойного безнейтринного бета-распадаДиаграмма Фейнмана двойного безнейтринного бета-распада
Состав Элементарная частица
Семья Фермион
Группа Истинно нейтральная частица
Участвует во взаимодействиях Гравитация
Античастица Сами себе
Теоретически обоснована Был впервые рассмотрен итальянским физиком Этторе Майораной в 1930-х годах[1]
В честь кого или чего названа Этторе Майорана и фермион
Квантовые числа
Электрический заряд 0
Цветной заряд 0
Барионное число 0
Лептонное число 0
B−L 0
Спин ½ ħ
Магнитный момент 0
Изотопический спин 0
Странность 0
Очарование 0
Прелесть 0
Истинность 0
Гиперзаряд 0

В физике элементарных частиц майора́новский фермио́н, или фермио́н Майора́ны — это фермион, который является своей собственной античастицей. Существование таких частиц было впервые рассмотрено итальянским физиком Этторе Майораной в 1937 году[1]. В экспериментах с полупроводниковыми нанопроволоками наблюдались квазичастицы, обладающие свойствами майорановского фермиона. Экспериментальное обнаружение майорановских частиц как в физике высоких энергий, так и в области физики твёрдого тела приведёт к важным последствиям для науки в целом[2].

В физике элементарных частиц

Предполагается, что нейтрино может быть либо фермионом Майораны, либо фермионом Дирака (в Стандартной модели все фермионы, включая нейтрино, являются дираковскими). Экспериментального подтверждения этого всё ещё нет, и теория Майораны, в итоге, может оказаться опровегнутой[3]. В первом случае различие между нейтрино и антинейтрино определяется только их спиральностью: превращение нейтрино в антинейтрино можно осуществить переворотом спина (или, например, переходом в систему отсчёта, в которой импульс нейтрино направлен в противоположном направлении, что, правда, осуществимо лишь при ненулевой массе нейтрино). Если электронное нейтрино является фермионом Майораны и при этом массивно, то некоторые изотопы могут испытывать безнейтринный двойной бета-распад; при существующей чувствительности экспериментов этот распад пока не обнаружен, хотя в мире проводятся десятки экспериментов по поиску этого процесса[4][5].

Гипотетические частицы нейтралино в суперсимметричных моделях являются фермионами Майораны. Поэтому открытие майорановских фермионов будет дополнительным аргументом для теорий суперсимметрии[6].

Майорановские частицы, в отличие от дираковских, не могут обладать магнитным дипольным моментом (кроме недиагональных компонент магнитного момента, изменяющих аромат)[7][8][9]. Слабое взаимодействие с электромагнитными полями делает майорановские фермионы кандидатами для частиц холодной тёмной материи[10][11].

16 июля 2013 года коллаборация GERDA сообщила[12], что в результате обработки данных первой фазы долговременного эксперимента, проводящегося в итальянской подземной лаборатории Гран-Сассо на криогенном полупроводниковом мультидетекторе, состоящем из германия, обогащённого германием-76, не был обнаружен безнейтринный двойной бета-распад этого изотопа (нижнее ограничение на период полураспада — не менее 3·1025 лет). Это, как и ряд более ранних и менее чувствительных экспериментов, свидетельствует в пользу того, что нейтрино не является майорановской частицей; точнее, ограничивает сверху так называемую майорановскую массу электронного нейтрино, которая для дираковского фермиона должна быть в точности равна нулю. Установленное верхнее ограничение равно приблизительно 0,2—0,4 эВ. В настоящее время ряд как действующих, так и находящихся на стадии планирования и разработки экспериментов по поиску безнейтринного двойного бета-распада нацелен на улучшение инструментальной чувствительности. Последние доступные данные для оценок снизу для полураспада и оценок сверху для массы приведены в таблице на март 2018 года[13].

Оценка параметров[14]
Эксперимент Изотоп Полураспад Масса
Gerda 76Ge 8,0·1025 лет 0,12—0,26 эВ
Majorana 76Ge 1,9·1025 лет 0,24—0,53 эВ
KamLAND-Zen 136Xe 10,7·1025 лет 0,05—0,16 эВ
EXO 136Xe 1,1·1025 лет 0,17—0,49 эВ
CUORE 130Te 1,5·1025 лет 0,11—0,50 эВ

Уравнение Дирака

Основная статья: Уравнение Майораны

Математически, фермионы со спином 1/2 описываются уравнением Дирака вида

[math]\displaystyle{ i\frac{\hbar}{c} \partial_t\psi(x, t) = [-i\hbar\boldsymbol{\alpha} \cdot \boldsymbol{\partial_x} + \beta mc]\psi(x, t), }[/math]

где m — масса частицы, а матрицы α и β удовлетворяют антикоммутационным соотношениям {αi, αj} = 2δij, {αi, β} = 0, β2 = 1. Так как выбор этих матриц неоднозначен, то их можно выбрать в виде

[math]\displaystyle{ \alpha_1 = \begin{pmatrix} 0 & \sigma_1 \\ \sigma_1 & 0 \end{pmatrix},\quad \alpha_2 = \begin{pmatrix} 0 & \sigma_3 \\ \sigma_3 & 0 \end{pmatrix},\quad \alpha_3 = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix},\quad \beta = \begin{pmatrix} 0 & \sigma_2 \\ \sigma_2 & 0 \end{pmatrix}, }[/math]

благодаря чему в исходном уравнении все коэффициенты получаются мнимыми. Тогда уравнение, сопряжённое уравнению Дирака, не меняется:

[math]\displaystyle{ i\frac{\hbar}{c} \partial_t\psi^*(x, t) = [-i\hbar\boldsymbol{\alpha} \cdot \boldsymbol{\partial_x} + \beta mc]\psi^*(x, t). }[/math]

Решению сопряжённого уравнения Дирака соответствует частица, которая является своей собственной античастицей ([math]\displaystyle{ \psi^*=\psi }[/math]) и называется майорановским фермионом[15]. Существует бесконечное множество матриц [math]\displaystyle{ \boldsymbol{\alpha} }[/math][16].

Решениями этого уравнения выступает четырёхкомпонентный спинор, но такую систему из четырёх уравнений Майораны можно привести к виду двух независимых систем (из двух уравнений каждая) с решениями в виде левых ([math]\displaystyle{ \psi_L }[/math]) и правых ([math]\displaystyle{ \psi_R }[/math]) майорановских фермионов. Причём массы (mL и mR) в этих новых частицах не обязательно совпадают[2]:

[math]\displaystyle{ (i\partial_t - \boldsymbol{p} \cdot \boldsymbol{\sigma}) \psi_R - im_R \sigma_2 \psi_R^* = 0, }[/math]
[math]\displaystyle{ (i\partial_t + \boldsymbol{p} \cdot \boldsymbol{\sigma}) \psi_L - im_L \sigma_2 \psi_L^* = 0. }[/math]

Эти уравнения можно получить, используя вариационный принцип в общем виде, исходя из лагранжиана электрослабого взаимодействия. Здесь интерес представляет выбор массового слагаемого в ланганжане, вид которого определяет дираковский или майорановский фермионы используются в теории[17]. Раньше такого вопроса не возникало из-за предположения о безмассовости нейтрино. Но открытие нейтринных осцилляций поставило вопрос о конечности масс этих истинно нейтральных фермионов. Если представить, что антинейтино и нейтрино на самом деле одна и та же частица (то есть майорановский фермион), то объяснение большой разницы в массах между нейтрино и другими лептонами может дать механизм качелей. Например, в этом случае, масса ненаблюдаемого экспериментально правого нейтрино велика по сравнению с массой электрона (mD), а масса левого составит малую величину порядка [math]\displaystyle{ m_D^2/m_R }[/math][18].

В физике твёрдого тела

Если в физике высоких энергий вопрос о существовании или несуществовании майорановских фермионов остаётся открытым, то никаких сомнений в существовании в сверхпроводниках аналогичных элементарных возбуждений, предсказанных теоретически, нет[3]. Вопрос заключается в демонстрации каких-либо связанных с ними наблюдаемых эффектов из-за технических сложностей[19]. Некоторые квазичастицы (различные возбуждения коллективных состояний в твердотельных системах, ведущие себя подобно частицам) могут описываться как майорановские фермионы, причём их существует несколько типов в связи с возможностью выбрать размерность системы. В физике твёрдого тела майорановские фермионы также называются майорановскими состояниями, чтобы отличать их от решения трёхмерного уравнения Майораны. Интерес к таким квазичастицам (предсказанным, но пока не открытым экспериментально) связан с тем, что они теоретически могут использоваться в кубитах для топологического квантового компьютера — например, для сохранения информации, — при этом из-за своей нелокальной природы они менее чувствительны к влиянию среды[19]. В одномерных системах говорят не о майорановских фермионах, а о майорановских локализованных состояниях, которые не перемещаются в системе свободно, благодаря чему сохраняют свои свойства из-за большого времени декогеренции[20]. Возможное экспериментальное обнаружение[21][22] таких объектов в комбинированных полупроводниковых-сверхпроводниковых наносистемах в сильном магнитном поле требует независимого подтверждения в связи со сложностью детектирования и существованием возможных альтернативных объяснений[23].

Майорановские фемионы могут существовать в экзотических системах, которые достаточно трудно реализуются на практике, например в p-волновых сверхпроводниках[24], полупроводниках в режиме дробного квантового эффекта Холла с фактором заполнением 5/2, на поверхности топологических изоляторов с использованием эффекта близости от s-волновых сверхпроводников[25], либо используя эффект близости между сверхпроводником и ферромагнетиком. С другой стороны, в 2010 году опубликовали две статьи, которые показали, как создать майорановские фермионы в полупроводниковых нанопроволоках[26][27].

Игрушечная модель Китаева

Рис. 1. Разбиение фермионов (первый ряд) на «полуфермионы» или майорановские фермионы в игрушечной модели Китаева в топологически тривиальном (второй ряд) и топологически нетрививальном (третий ряд) случаях[28].

Алексей Китаев[29] предложил рассмотреть гамильтониан бесспинового p-волнового сверхпроводника в терминах вторичного квантования[30]

[math]\displaystyle{ H_K=\sum_{j=1}^N\left(-t(a_j^{\dagger}a_{j+1}+a_{j+1}^{\dagger}a_j)-\mu\left(a_j^{\dagger}a_j-\frac{1}{2}\right)+\Delta e^{i\theta}a_ja_{j+1}+\Delta e^{-i\theta}a_{j+1}^{\dagger}a_j^{\dagger}\right)\,, }[/math]

где t — интеграл перескока, μ — химический потенциал, Δ и θ — амплитуда и фаза параметра порядка. Можно ввести следующие майорановские фермионные операторы для этой задачи [math]\displaystyle{ c_{2j-1}=e^{i\theta/2}a_j+e^{-i\theta/2}a_j^{\dagger} }[/math] и [math]\displaystyle{ c_{2j}=-i\left(e^{i\theta/2}a_j-e^{-i\theta/2}a_j^{\dagger}\right) }[/math], которые приводят к новому виду гамильтониана

[math]\displaystyle{ H_K=\frac{-i}{2}\sum_{j=1}^N\mu c_{2j-1}c_{2j}+\frac{i}{2}\sum_{j=1}^{N-1}[(t+\Delta)c_{2j}c_{2j+1}+(-t+\Delta)c_{2j-1}c_{2j+2}]\,. }[/math]

Теперь рассмотрим два предельных случая что проиллюстрировано на рис. 1: в первом случае химический потенциал меньше нуля, μ<0, а остальные параметры обращаются в ноль, Δ=t=0. Тогда спаривание полуфермионов в фермионы происходит тривиальным образом для каждого узла цепочки. Во втором случае, когда химический потенциал равен нулю, μ=0, а интеграл перескока и параметр порядка равны, Δ=t>0, то сумма превращается в слагаемые спаривающие полуфермионы в соседних узлах, причём крайние полуфермионы выпадают из суммы и образуют дважды вырожденный уровень при нуле энергии. Эти два узла можно превратить в обычный фермион сильно нелокальной природы [math]\displaystyle{ f=1/2(c_1+ic_N) }[/math]. А гамильтониан приобретает обычный диагональный вид при преобразовании [math]\displaystyle{ d_j=1/2(c_{2j}+ic_{2j+1}) }[/math], [math]\displaystyle{ d_j=1/2(c_{2j}-ic_{2j+1}) }[/math][28]:

[math]\displaystyle{ H_t=2t\sum_{j=1}^{L-1}\left(d_j^{\dagger}d_{j}-\frac{1}{2}\right)\,. }[/math]

Фактически эта задача не имеет отношения к реальности, но показывает как получить майорановские связные состояния и какой гамильтониан во взаимодействующей системе должен появиться. В качестве возможного материала для реализации майорановских состояний Китаев предложил использовать нанопроволоки из p-волнового сверхпроводника, то есть одномерные свехпроводники с триплетным состояниями куперовских пар.

Полупроводниковые нанопроволоки

Файл:Majorana.ogg
Рис. 2. Формирование топологического закона дисперсии используя ур. 2 при последовательном включении спин-орбитального взаимодействия, сверхпроводимости и приложении магнитного поля.

В работах 2010 года[31][32] наметился путь реализации майорановских фермионов на практике. Основное достижение заключалось в понимании влияния различных эффектов на майорановские связные состояния. В работе[31] рассматривался гамильтониан (постоянная Планка равна единице) вида

[math]\displaystyle{ H=\int\Psi^{\dagger}\left[\left(\frac{k^2}{2m}-\mu\right)\tau_z\otimes\sigma_0+\alpha k\tau_z\otimes\sigma_z+\Delta_Z\tau_0\otimes\sigma_x+\Delta_{sc}\tau_x\otimes\sigma_0\right]\Psi dy, }[/math] (1)

где волновая функция имеет вид [math]\displaystyle{ \Psi^{\dagger}=(\psi^{\dagger}_{\uparrow},\psi^{\dagger}_{\downarrow},\psi_{\downarrow},-\psi_{\uparrow}) }[/math]. Первое слагаемое в подынтегральном выражении отвечает за кинетическую энергию частиц с учётом химического потенциала, второе — спин-орбитальное взаимодействие, третье — зеемановская энергия, четвёртое — сверхпроводимость. Нанопроволока ориентирована в направлении y, спин-орбитальное взаимодействие вдоль x, а магнитное поле вдоль z. Матрицы Паули [math]\displaystyle{ \sigma }[/math], [math]\displaystyle{ \tau }[/math] действуют в спиновом пространстве и в пространстве частиц-античастиц. Индекс 0 отвечает за единичную матрицу. Гамильтониан имеет собственные значения вида

[math]\displaystyle{ E_{\pm}^2=\Delta_Z^2+\Delta_{sc}^2+\left(\frac{k^2}{2m}-\mu\right)^2+(\alpha k)^2\pm 2\sqrt{\Delta_Z^2\Delta_{sc}^2+\left(\frac{k^2}{2m}-\mu\right)^2\left((\alpha k)^2+\Delta_Z^2\right)}. }[/math] (2)

Вблизи нуля волнового вектора возникает запрещённая зона [math]\displaystyle{ \Delta=|\Delta_Z-\sqrt{\Delta_{sc}^2+\mu^2}| }[/math]. Когда выполняется условие [math]\displaystyle{ \Delta_Z\gt \sqrt{\Delta_{sc}^2+\mu^2} }[/math] говорят о возникновении топологически нетривиальной фазы, а точка, где ширина зоны равна нулю — точкой топологического фазового перехода. Она разделяет топологически тривиальную и нетривиальную фазы. Когда выполняется условие на существование топологически нетривиальной фазы на обоих краях нанопроволоки возникают майорановские связанные состояния при нуле энергии. На рис. 2 показано как возникает четыре ветви дисперсионных соотношений из ур. 2 при последовательном включении взаимодействий. Спин-орбитальное взаимодействие вида αk приводит к расщеплению параболического закона дисперсии для нанопроволоки. При добавлении сверхпроводимости добавляется электрон-дырочная симметрия, что удваивает количество дисперсионных кривых и возникает сверхпроводящая щель [math]\displaystyle{ \Delta_{sc} }[/math] в спектре возбуждений. При приложении магнитного поля появляется зеемановское расщепление уровней [math]\displaystyle{ \Delta_Z }[/math], которое работает против сверхпроводимости и закрывает щель. При равенстве [math]\displaystyle{ \Delta_Z=\Delta_{sc} }[/math] (химический потенциал [math]\displaystyle{ \mu=0 }[/math]) достигается точка фазового перехода и щель пропадает, но при дальнейшем увеличении магнитного поля щель появляется вновь. Эта щель соответствует состоянию топологической сверхпроводимости[31].

Модель Фу — Кейна

В двумерном случае реализация майорановских фермионов оказалась возможна в модели предложенной учёными Лян Фу и Чарльзом Кейном в 2008 году[33]. Использовав модель топологического изолятора (проводимость в таких материалах существует только на поверхности) с нанесённым на его поверхность тогкого слоя сверхпроводника s-типа, они рассмотрели гамильтониан для волновой функции (в формализме Намбу) [math]\displaystyle{ \Psi=((\psi_{\uparrow},\psi_{\downarrow}),(\psi^{\dagger}_{\uparrow},-\psi^{\dagger}_{\downarrow}))^{T} }[/math], где стрелками обозначены проекции спина, а индекс T отвечает за транспонирование, вида[34]

[math]\displaystyle{ H=-iv\tau^z\boldsymbol{\sigma}\cdot\boldsymbol{\nabla}-\mu I\tau^z+\Delta_0I(\tau^x\cos(\phi)+\tau^y\sin(\phi))\,, }[/math]

где v — скорость электрона на уровне энергии Ферми (фермиевская скорость), I — единичная матрица, σ=(σx,σy) — двумерный вектор составленный из матриц Паули, действующие на спиновые состояния, τx и τy — матрицы Паули действующие на пары [math]\displaystyle{ \psi }[/math] и [math]\displaystyle{ \psi^{\dagger} }[/math], смешивая их между собой, μ — химический потенциал, Δ0 — параметр порядка сверхпроводника. Блочная часть гамильтониана [math]\displaystyle{ H_0=-iv\boldsymbol{\sigma}\cdot\boldsymbol{\nabla}-\mu I }[/math] — это гамильтониан для квазичастиц возникающий на поверхности топологического изолятора. Куперовские пары из сверхпроводника из-за эффекта близости могут находиться на поверхности тополонического изолятора, приводя к эффективному гамильтониану взаимодействию аналогичному сверхпроводнику p-типа, где по теории Китаева существуют майорановские фермионы. Отличие состояит в симметрии этого гамильтониана по отношению к обращению времени, что приводит к дополнительному вырождению. Но используя внешнее магнитное поле ориентированное перпендикулярно поверхности сверхпроводника, которое нарушает симметрию по обращению времени, возможно сформировать сверхпроводящие вихри в рассматриваемой системе. Рассчёт показывает, что майорановский фермион возникает в ядре вихря[33].

Примечания

  1. ↑ 1,0 1,1 E. Majorana.  // Nuovo Cimento. — 1937. — Vol. 14. — P. 171.
  2. ↑ 2,0 2,1 Elliott & Franz, 2015, с. 138.
  3. ↑ 3,0 3,1 Elliott & Franz, 2015, с. 139.
  4. ↑ Rodejohann, Werner. Neutrino-less double beta decay and particle physics (англ.) // International Journal of Modern Physics[англ.] : journal. — 2011. — Vol. E20, no. 9. — P. 1833—1930. — doi:10.1142/S0218301311020186. — Bibcode: 2011IJMPE..20.1833R. — arXiv:1106.1334.
  5. ↑ Schechter, J.; Valle, J. W. F. Neutrinoless double-β decay in SU(2) × U(1) theories (англ.) // Physical Review D : journal. — 1982. — Vol. 25, no. 11. — P. 2951—2954. — doi:10.1103/PhysRevD.25.2951. — Bibcode: 1982PhRvD..25.2951S.
  6. ↑ Palash B. Pal. Dirac, Majorana, and Weyl fermions // Am. J. Phys.. — 2011. — Т. 79. — С. 485. — doi:10.1119/1.3549729. — arXiv:1006.1718.
  7. ↑ Kayser, Boris; Goldhaber, Alfred S. CPT and CP properties of Majorana particles, and the consequences (англ.) // Physical Review D : journal. — 1983. — Vol. 28, no. 9. — P. 2341—2344. — doi:10.1103/PhysRevD.28.2341. — Bibcode: 1983PhRvD..28.2341K.
  8. ↑ Radescu, E. E. On the electromagnetic properties of Majorana fermions (англ.) // Physical Review D : journal. — 1985. — Vol. 32, no. 5. — P. 1266—1268. — doi:10.1103/PhysRevD.32.1266. — Bibcode: 1985PhRvD..32.1266R.
  9. ↑ Boudjema, F.; Hamzaoui, C.; Rahal, V.; Ren, H. C. Electromagnetic Properties of Generalized Majorana Particles (англ.) // Physical Review Letters : journal. — 1989. — Vol. 62, no. 8. — P. 852—854. — doi:10.1103/PhysRevLett.62.852. — Bibcode: 1989PhRvL..62..852B. — PMID 10040354.
  10. ↑ Pospelov, Maxim; ter Veldhuis, Tonnis. Direct and indirect limits on the electro-magnetic form factors of WIMPs (англ.) // Physics Letters B[англ.] : journal. — 2000. — Vol. 480, no. 1—2. — P. 181—186. — doi:10.1016/S0370-2693(00)00358-0. — Bibcode: 2000PhLB..480..181P. — arXiv:hep-ph/0003010.
  11. ↑ Ho, Chiu Man; Scherrer, Robert J. Anapole Dark Matter (англ.) // Physics Letters B[англ.] : journal. — 2013. — Vol. 722, no. 8. — P. 341—346. — doi:10.1016/j.physletb.2013.04.039. — Bibcode: 2013PhLB..722..341H. — arXiv:1211.0503.
  12. ↑ GERDA Collaboration. Results on Neutrinoless Double-β Decay of 76Ge from Phase I of the GERDA Experiment // Phys. Rev. Lett.. — 2013. — Т. 111. — С. 122503. — doi:10.1103/PhysRevLett.111.122503. — arXiv:1307.4720.
  13. ↑ GERDA, 2018.
  14. ↑ GERDA Collaboration. Improved Limit on Neutrinoless Double-β Decay of 76Ge from GERDA Phase II // Phys. Rev. Lett.. — 2018. — Т. 120. — С. 132503. — doi:10.1103/PhysRevLett.120.132503.
  15. ↑ Sato M., Ando Y. Топологические сверхпроводники: обзор. // Rep. Prog. Phys.. — 2017. — Т. 80. — С. 076501. — doi:10.1088/1361-6633/aa6ac7. — arXiv:1608.03395.
  16. ↑ Pal, 2011.
  17. ↑ Elliott & Franz, 2015, с. 141.
  18. ↑ Elliott & Franz, 2015, с. 144.
  19. ↑ 19,0 19,1 Elliott & Franz, 2015, с. 140.
  20. ↑ V. Mourik, K. Zuo, S. M. Frolov, S. R. Plissard, E. P. A. M. Bakkers, L. P. Kouwenhoven. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices // Science. — 2012. — Т. 336. — С. 1003—1007. — doi:10.1126/science.1222360. — arXiv:1204.2792.
  21. ↑ A. D. K. Finck et al. Anomalous Modulation of a Zero-Bias Peak in a Hybrid Nanowire-Superconductor Device // Phys. Rev. Lett. — 2013. — Vol. 110. — P. 126406. — doi:10.1103/PhysRevLett.110.126406.
  22. ↑ Mourik et al., 2012, с. 1007.
  23. ↑ Davide Castelvecchi. Evidence of elusive Majorana particle dies — but computing hope lives on // Nature. — 2021. — Т. 591. — С. 354—355. — doi:10.1038/d41586-021-00612-z.
  24. ↑ Kitaev A. Yu. Unpaired Majorana fermions in quantum wires = Неспаренные майорановские фермионы в квантовых проволоках // Phys.-Usp.. — 2001. — Т. 44. — С. 131. — doi:10.1070/1063-7869/44/10S/S29. — arXiv:cond-mat/0010440.
  25. ↑ Fu L., Kane C. L. Сверхпроводящий эффект близости и майорановские фермионы на поверхности топологического изолятора = Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator // Phys. Rev. Lett.. — 2008. — Т. 100. — С. 096407. — doi:10.1103/PhysRevLett.100.096407. — arXiv:0707.1692.
  26. ↑ Oreg Y., Refael G., von Oppen F. Helical Liquids and Majorana Bound States in Quantum Wires // Phys. Rev. Lett.. — 2010. — Т. 105. — С. 177002. — doi:10.1103/PhysRevLett.105.177002. — arXiv:1003.1145.
  27. ↑ Lutchyn R. M., Sau J. D., Das Sarma S. Майорановские фермионы и топологический фазовый переход в гетероструктурах полупроводник-сверхпроводник. = Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures // Phys. Rev. Lett.. — 2010. — Т. 105. — С. 077001. — doi:10.1103/PhysRevLett.105.077001. — arXiv:1002.4033.
  28. ↑ 28,0 28,1 Kitaev A., 2001, с. 133.
  29. ↑ Kitaev A., 2001.
  30. ↑ Kitaev A., 2001, с. 132.
  31. ↑ 31,0 31,1 31,2 Oreg Y., 2010, с. 177002.
  32. ↑ Lutchyn R. M., 2010, с. 077001.
  33. ↑ 33,0 33,1 Fu & Kane, 2008.
  34. ↑ Fu & Kane, 2008, с. 1.

Литература


Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Майорановский_фермион&oldid=7036048