Эффект Зеемана

Эффе́кт Зе́емана^[1] — расщепление линий атомных спектров в магнитном поле. Назван в честь Питера Зеемана, открывшего эффект в 1896 году.

Эффект обусловлен тем, что в присутствии магнитного поля [math]\displaystyle{ \vec{B} }[/math] электрон, обладающий магнитным моментом [math]\displaystyle{ \vec{\mu}, }[/math] приобретает дополнительную энергию [math]\displaystyle{ \Delta E= -\vec{\mu}\cdot\vec{B}. }[/math] Приобретённая энергия приводит к снятию вырождения атомных состояний по полному квантовому числу [math]\displaystyle{ m_j }[/math] и расщеплению атомных спектральных линий.

Природа эффекта

В классическом представлении

Объяснение эффекта Зеемана в рамках классической физики было дано Хендриком Лоренцем. Согласно его теории, атом рассматривается как классический гармонический осциллятор, и его уравнение движения в присутствии магнитного поля [math]\displaystyle{ \vec{B}, }[/math] направленного вдоль оси Z, можно рассматривать в виде

[math]\displaystyle{ m_e\frac{d\vec{v}}{dt}=-m_e\omega_0^2 \vec{r} - e\vec{v}\times \vec{B}, }[/math]

где [math]\displaystyle{ \vec{v} }[/math] — скорость вращения электрона вокруг ядра, [math]\displaystyle{ m_e }[/math] — масса электрона, [math]\displaystyle{ \omega_o }[/math] — резонансная частота электронного дипольного перехода. Последний член в уравнении обусловлен силой Лоренца.

Введём величину, называемую ларморовской частотой [math]\displaystyle{ \Omega_L=\frac{eB}{2m_e}. }[/math]

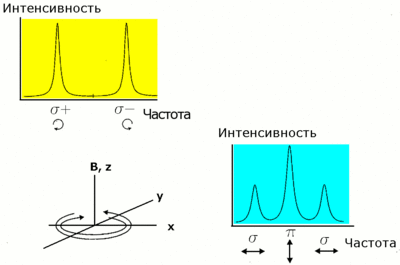
Поляризация и спектр Зееман-эффекта, детектируемые с различных направлений наблюдения: * картинка с жёлтым фоном — наблюдение ведётся в направлении магнитного поля. В этом случае в спектре флуоресценции атомарных паров детектируется две частоты c круговой поляризацией [math]\displaystyle{ \sigma^+ }[/math] и [math]\displaystyle{ \sigma^- }[/math] * картинка с синим фоном — наблюдение ведётся перпендикулярно направлению магнитного поля. В этом случае в спектре флуоресценции атомарных паров детектируются три частоты, имеющие линейную поляризацию σ и π

Решение уравнения движения показывает, что резонансная частота дипольного момента в присутствии магнитного поля расщепляется на три частоты [math]\displaystyle{ \omega\simeq \omega_o\pm \Omega_L }[/math], называемых лоренцевским или простым зеемановским триплетом. Таким образом, в магнитном поле электрон вместо простого вращения вокруг ядра атома начинает совершать сложное движение относительно выделенного магнитным полем направления [math]\displaystyle{ Z. }[/math] Электронное облако атома прецессирует вокруг этой оси с частотой Лармора [math]\displaystyle{ \Omega_L. }[/math]

Такая простая модель объясняет наблюдаемое в экспериментах изменение поляризации флуоресценции атомарных паров в зависимости от направления наблюдения. Если смотреть вдоль оси Z, то на частоте [math]\displaystyle{ \omega_o }[/math] никакой атомной флуоресценции наблюдаться не будет, так как атомный диполь на этой частоте колеблется вдоль оси магнитного поля, а его излучение распространяется в направлении, перпендикулярном этой оси. На частотах [math]\displaystyle{ \omega\simeq \omega_o\pm\Omega_L }[/math] наблюдается право- и левовращающая поляризации, так называемые [math]\displaystyle{ \sigma^+ }[/math] и [math]\displaystyle{ \sigma^- }[/math]-поляризации.

Если же смотреть вдоль осей X или Y, то наблюдается линейная поляризация (π и σ соответственно) на всех трёх частотах [math]\displaystyle{ \omega_o }[/math] и [math]\displaystyle{ \omega\simeq \omega_o\pm \Omega_L }[/math]. Вектор поляризации света π направлен вдоль магнитного поля, а σ — перпендикулярно.

Классическая физика оказалась способной описать только так называемый простой (нормальный) эффект Зеемана. Объяснить сложный (аномальный) эффект Зеемана в рамках классических представлений о природе невозможно.

В квантовом представлении

Полный гамильтониан атома в магнитном поле имеет вид:

[math]\displaystyle{ H = H_0 + V_M,\ }[/math]

где [math]\displaystyle{ H_0 }[/math] — невозмущенный гамильтониан атома и [math]\displaystyle{ V_M }[/math] — возмущение, созданное магнитным полем:

[math]\displaystyle{ V_M = -\vec{\mu} \cdot \vec{B}. }[/math]

Здесь [math]\displaystyle{ \vec{\mu} }[/math] — магнитный момент атома, который состоит из электронной и ядерной частей. Ядерным магнитным моментом, который на несколько порядков меньше электронного, можно пренебречь. Следовательно,

[math]\displaystyle{ \vec{\mu} = -\mu_B g \vec{J}/\hbar, }[/math]

где [math]\displaystyle{ \mu_B }[/math] — магнетон Бора, [math]\displaystyle{ \vec{J} }[/math] — полный электронный угловой момент, и [math]\displaystyle{ g }[/math] — фактор.

Оператор магнитного момента электрона является суммой орбитального [math]\displaystyle{ \vec L }[/math] и спинового [math]\displaystyle{ \vec S }[/math] угловых моментов, умноженных на соответствующие гиромагнитные отношения:

[math]\displaystyle{ \vec{\mu} = -\mu_B (g_l \vec{L} + g_s \vec{S})/\hbar, }[/math]

где [math]\displaystyle{ g_l = 1 }[/math] и [math]\displaystyle{ g_s \approx 2{,}0023192 }[/math]; последнюю величину называют аномальным гиромагнитным отношением; отклонение от 2 появляется из-за квантово-электродинамических эффектов. В случае L-S-связи для расчета полного магнитного момента суммируются все электроны:

[math]\displaystyle{ g \vec{J} = \left\langle\sum_i (g_l \vec{l_i} + g_s \vec{s_i})\right\rangle = \left\langle (g_l\vec{L} + g_s \vec{S})\right\rangle, }[/math]

где [math]\displaystyle{ \vec{L} }[/math] и [math]\displaystyle{ \vec{S} }[/math] — полный орбитальный и спиновый моменты атома, и усреднение делается по атомному состоянию с данной величиной полного углового момента.

Простой эффект Зеемана

Простым или нормальным эффектом Зеемана называется расщепление спектральных линий на три подуровня; он качественно может быть объяснён классически. Если член взаимодействия [math]\displaystyle{ V_M }[/math] мал (меньше тонкой структуры то есть [math]\displaystyle{ V_M\ll|E_i-E_k| }[/math]), нормальный эффект Зеемана наблюдается:

при переходах между синглетными термами ([math]\displaystyle{ S=0; J=L }[/math]);
при переходах между уровнями [math]\displaystyle{ L=0 }[/math] и [math]\displaystyle{ J=S }[/math];
при переходах между уровнями [math]\displaystyle{ J=1 }[/math] и [math]\displaystyle{ J=0 }[/math], поскольку [math]\displaystyle{ J=0 }[/math] не расщепляется, а [math]\displaystyle{ J=1 }[/math] расщепляется на три подуровня.

В сильных полях также наблюдается расщепление на три подуровня, однако это может происходить вследствие эффекта Пашена — Бака (см. далее).

При нормальном эффекте Зеемана расщепление связано с чисто орбитальным или чисто спиновым магнитным моментами. Это наблюдается в синглетах He и в группе щёлочноземельных элементов, а также в спектрах Zn, Cd, Hg.

Поляризация [math]\displaystyle{ \pi }[/math] и [math]\displaystyle{ \sigma^{\pm} }[/math] наблюдаются при изменении проекции магнитного момента на [math]\displaystyle{ \Delta m_j=0 }[/math] и [math]\displaystyle{ \Delta m_j=\pm1 }[/math], соответственно.

Несмотря на то, что Зееман изначально наблюдал в своих экспериментах именно простой эффект, в природе он встречается относительно редко.

Сложный эффект Зеемана

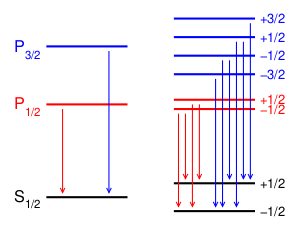
Для всех несинглетных линий спектральные линии атома расщепляются на значительно большее, чем три, количество компонент, а величина расщепления кратна нормальному расщеплению [math]\displaystyle{ \nu_n }[/math]. В случае сложного (или аномального) эффекта величина расщепления сложным образом зависит от квантовых чисел [math]\displaystyle{ L, ~S, ~J }[/math]. Как указано ранее, приобретённая электроном в магнитном поле дополнительная энергия [math]\displaystyle{ V_M }[/math] пропорциональна [math]\displaystyle{ g }[/math] — фактору, который называют множителем Ланде (гиромагнитный множитель) и который дается формулой

[math]\displaystyle{ g=1+\frac{J(J+1)-L(L+1)+S(S+1)}{2J(J+1)}, }[/math]

где L — значение орбитального момента атома, S — значение спинового момента атома, J — значение полного момента.

Впервые этот множитель ввёл Ланде. Работы Ланде являлись продолжением работ Зеемана, поэтому расщепление линий в спектрах, полученных Ланде в магнитном поле, называют аномальным эффектом Зеемана. Заметим, что эксперимент Зеемана сделан при [math]\displaystyle{ L=J, S=0 }[/math], то есть [math]\displaystyle{ g=1 }[/math], поэтому никакой надобности в множителях не возникало.

Таким образом, вырожденный энергетический уровень расщепляется на [math]\displaystyle{ 2J + 1 }[/math] равноотстоящих зеемановских подуровня (где [math]\displaystyle{ J }[/math] — максимальное значение модуля магнитного квантового числа [math]\displaystyle{ m_l = j }[/math]).

Эффект Пашена — Бака

Эффект Пашена — Бака наблюдается, когда зеемановское расщепление превышает расщепление тонкой структуры, то есть при [math]\displaystyle{ V_M\gg|E_i-E_k| }[/math]. В таких полях разрушается обычное спин-орбитальное взаимодействие. При этом сложное зеемановское расщепление переходит в простое, так что вырожденный энергетический уровень расщепляется на [math]\displaystyle{ 2J + 1 }[/math] равноотстоящих зеемановских подуровней (где [math]\displaystyle{ J }[/math] — максимальное значение модуля магнитного квантового числа [math]\displaystyle{ m_l = j }[/math]).

Сверхсильные поля

В ещё более сильных магнитных полях, при которых циклотронная энергия электрона [math]\displaystyle{ \hbar\omega_c }[/math] (где [math]\displaystyle{ \omega_c }[/math] — его циклотронная частота) становится сопоставимой с энергией связи атома или превышает её, структура атома полностью меняется. В этом случае классификация уровней производится согласно уровням Ландау, а кулоновское взаимодействие выступает как возмущение по отношению к магнитному, расщепляя уровни Ландау на подуровни. Для атома водорода в основном состоянии такая ситуация наступает, когда [math]\displaystyle{ \hbar\omega_c }[/math] превышает атомную единицу энергии, то есть при [math]\displaystyle{ B\gt 2,35\times10^5 }[/math] Тл.

История

Предположение, что спектральные линии могут расщепляться в магнитном поле, было впервые высказано Майклом Фарадеем, который, однако, не смог наблюдать эффект из-за отсутствия источника достаточно сильного поля^[2]. Эффект был впервые обнаружен Питером Зееманом в 1896 году для узкой зелёно-голубой линии кадмия. В своём опыте Зееман применял магнитные поля напряжённостью 1–1,5 Тл и наблюдал расщепление линии на триплет. Зееман сослался на Фарадея как на автора идеи^[2]. 31 октября 1897 года об этих опытах узнал Хендрик Лоренц, который уже на следующий день встретился с Зееманом и привёл ему своё объяснение, основанное на разработанной им же классической электронной теории. Вскоре, однако, обнаружилось, что спектральные линии большинства других веществ расщепляются в магнитном поле более сложным образом. Объяснить этот эффект удалось только в рамках квантовой физики с развитием представлений о спине^[3]. За открытие и объяснение эффекта Зееман и Лоренц были награждены Нобелевской премией по физике 1902 года.

См. также

Примечания

↑ Ельяшевич М. А. Зеемана эффект // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 77—78. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ ^2,0 ^2,1 Zeeman P. The Effect of Magnetisation on the Nature of Light Emitted by a Substance (англ.) // Nature. — 1897. — Vol. 55, iss. 1424. — P. 347. — doi:10.1038/055347a0. — Bibcode: 1897Natur..55..347Z.
↑ Сивухин Д. В. § 92. Эффект Зеемана // Общий курс физики. — М.: Наука, 1980. — Т. IV. Оптика. — С. 564. — 768 с.

Литература

Сивухин Д. В. Атомная и ядерная физика // Общий курс физики. — М.: Физматлит, 2002. — Т. 5. — 784 с.
Шпольский Э. В. Атомная физика (в 2-х томах). — М.: Наука, 1984. — 990 с.
Christopher J. Foot. Atomic Physics. — 2004. — ISBN 13: 9780198506966.
М. А. Ельяшевич. Зеемана эффект // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия (т. 1—2); Большая Российская энциклопедия (т. 3—5), 1988—1999. — ISBN 5-85270-034-7.

Оригинальные статьи

P. Zeeman. On the influence of Magnetism on the Nature of the Light emitted by a Substance (англ.) // Phil. Mag.. — 1897. — Vol. 43. — P. 226.
P. Zeeman. Doubles and triplets in the spectrum produced by external magnetic forces (англ.) // Phil. Mag.. — 1897. — Vol. 44. — P. 55.
P. Zeeman. The Effect of Magnetisation on the Nature of Light Emitted by a Substance (англ.) // Nature. — 1897. — Vol. 55. — P. 347. — doi:10.1038/055347a0.

[ФЭ-1] Ельяшевич М. А. Зеемана эффект // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 77—78. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.

[origseem-2] 2,0 ^2,1 Zeeman P. The Effect of Magnetisation on the Nature of Light Emitted by a Substance (англ.) // Nature. — 1897. — Vol. 55, iss. 1424. — P. 347. — doi:10.1038/055347a0. — Bibcode: 1897Natur..55..347Z.

[3] Сивухин Д. В. § 92. Эффект Зеемана // Общий курс физики. — М.: Наука, 1980. — Т. IV. Оптика. — С. 564. — 768 с.

[1]

[2]

[3]