Резонансы
Резонанс (резонон[1]) — короткоживущие возбуждённые состояния адронов. Большинство известных частиц являются резонансами.
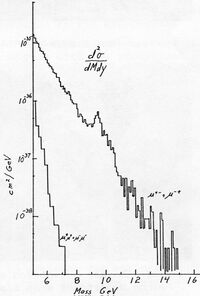
Время жизни резонансов: 10−22—10−24 с, поэтому их невозможно наблюдать непосредственно в виде треков на детекторах. Они определяются как пики в полном сечении образования вторичных частиц:
- [math]\displaystyle{ \sigma(E)=\sigma_0\frac{\left(\frac{\Gamma}{2}\right)^2}{(E-E_0)^2+\left(\frac{\Gamma}{2}\right)^2} }[/math]
Максимальное сечение [math]\displaystyle{ \sigma(E_0)=\sigma_0 }[/math] соответствует резонансу с энергией [math]\displaystyle{ E_0 }[/math] и шириной [math]\displaystyle{ \Gamma }[/math]. Ширина резонанса, выражаемая в единицах энергии соответствует его среднему времени жизни [math]\displaystyle{ \tau }[/math]:
- [math]\displaystyle{ \tau=\frac{\hbar}{\Gamma} }[/math]
Резонансы аналогичны возбуждённым состояниям атома: когда электрон поглощает энергию и переходит на другой более высокий энергетический уровень. Подобные возбуждённые состояния, называемые изомерами, существуют и у атомных ядер. Аналогично электрону в атоме или нуклону в ядре, кварки, получая достаточную порцию энергии, также переходят на другой энергетический уровень. Обычные же (метастабильные) частицы при этом являются основными состояниями кварковой системы. Соответственно, резонансы можно описывать спектральными термами [math]\displaystyle{ n^{2S+1}L_J }[/math], где:
- [math]\displaystyle{ n }[/math] — главное квантовое число,
- [math]\displaystyle{ S }[/math] — спиновое квантовое число (0 или 1 — для мезонов, 1⁄2 или 3⁄2 — для барионов),
- [math]\displaystyle{ L }[/math] — орбитальное квантовое число,
- [math]\displaystyle{ J=|L\pm S| }[/math] — внутреннее квантовое число (соответствует спину самого резонанса).
В отличие от электрического поля внутри атома, теория которого довольно проста, кварки находятся в глюонном поле, расчёт которого представляет довольно большую сложность. Поэтому крайне сложно заранее предсказать спектр возбуждения кварковой системы, хотя в большинстве случаев он хорошо описывается теорией полюсов Редже[2]. Также среди резонансов, помимо чистых [math]\displaystyle{ q\tilde{q} }[/math] и [math]\displaystyle{ qqq }[/math] состояний, встречаются также системы с дополнительными кварками (тетракварк, пентакварк) и глюонной примесью (глюбол). В связи с этим каждый новый резонанс до сих пор является своего рода сюрпризом для физиков.
Номенклатура резонансов
Резонансы обозначаются как и обычные частицы, но за символом в скобках указывается их масса в МэВ. Раньше символ резонанса дополнялся звёздочкой, но сейчас она редко используется.
Для нейтральных мезонов, тетракварков, экзотических мезонов и их резонансов принята следующая схема обозначения:[3]
| [math]\displaystyle{ I }[/math] | Кварковый состав | J PC | |||
|---|---|---|---|---|---|
| (0, 1…)− + | (0, 1…)+ − | (0, 1…)− − | (0, 1…)+ + | ||
| [math]\displaystyle{ I=1 }[/math] | [math]\displaystyle{ \mathrm{u\tilde{u}} }[/math] и [math]\displaystyle{ \mathrm{d\tilde{d}} }[/math] | [math]\displaystyle{ \pi }[/math] | [math]\displaystyle{ b }[/math] | [math]\displaystyle{ \rho }[/math] | [math]\displaystyle{ a }[/math] |
| [math]\displaystyle{ \mathrm{c\tilde{c}} }[/math] | [math]\displaystyle{ \Pi_c }[/math] | [math]\displaystyle{ Z_c }[/math] | [math]\displaystyle{ R_c }[/math] | [math]\displaystyle{ W_c }[/math] | |
| [math]\displaystyle{ \mathrm{b\tilde{b}} }[/math] | [math]\displaystyle{ \Pi_b }[/math] | [math]\displaystyle{ Z_b }[/math] | [math]\displaystyle{ R_b }[/math] | [math]\displaystyle{ W_b }[/math] | |
| [math]\displaystyle{ \mathrm{t\tilde{t}} }[/math] | [math]\displaystyle{ \Pi_t }[/math] | [math]\displaystyle{ Z_t }[/math] | [math]\displaystyle{ R_t }[/math] | [math]\displaystyle{ W_t }[/math] | |
| [math]\displaystyle{ I=0 }[/math] | [math]\displaystyle{ \mathrm{u\tilde{u}} }[/math], [math]\displaystyle{ \mathrm{d\tilde{d}} }[/math] и/или [math]\displaystyle{ \mathrm{s\tilde{s}} }[/math] | [math]\displaystyle{ \eta, \eta' }[/math] | [math]\displaystyle{ h, h' }[/math] | [math]\displaystyle{ \omega, \phi }[/math] | [math]\displaystyle{ f, f' }[/math] |
| [math]\displaystyle{ \mathrm{c\tilde{c}} }[/math] | [math]\displaystyle{ \eta_c }[/math] | [math]\displaystyle{ h_c }[/math] | [math]\displaystyle{ J/\psi,\psi }[/math] | [math]\displaystyle{ \chi_c }[/math] | |
| [math]\displaystyle{ \mathrm{b\tilde{b}} }[/math] | [math]\displaystyle{ \eta_b }[/math] | [math]\displaystyle{ h_b }[/math] | [math]\displaystyle{ \Upsilon }[/math] | [math]\displaystyle{ \chi_b }[/math] | |
| [math]\displaystyle{ \mathrm{t\tilde{t}} }[/math] | [math]\displaystyle{ \eta_t }[/math] | [math]\displaystyle{ h_t }[/math] | [math]\displaystyle{ \theta }[/math] | [math]\displaystyle{ \chi_t }[/math] | |
Примечания
- ↑ Теория кварков, 1971, с. 5.
- ↑ В.В. Анисович. Систематизация кварк-антикварковых состояний и экзотические мезоны // Успехи физических наук : журнал. — 2004. — Январь (т. 174, № 1). — С. 49–72. — doi:10.3367/UFNr.0174.200401d.0049.
- ↑ Naming scheme for hadrons. Дата обращения: 24 февраля 2021. Архивировано 20 марта 2021 года.
Литература
- Резонансы — статья из Физической энциклопедии
- Коккедэ Я. Теория кварков. — М.: Мир, 1971. — 341 с.