Риман, Бернхард
| Георг Фридрих Бернхард Риман | |
|---|---|
 | |
| Место рождения | Брезеленц, Ганновер |
| Место смерти | Селаска, Пьемонт |
| Научная сфера | математика, механика, физика |
| Место работы | Гёттингенский университет |
| Альма-матер | Гёттингенский университет |
| Научный руководитель | К. Ф. Гаусс |
| Ученики | Шеринг, Эрнст |
| Известен как | основатель римановой геометрии |
Гео́рг Фри́дрих Бе́рнхард Ри́ман (иногда Бернгард, нем. Georg Friedrich Bernhard Riemann; 17 сентября 1826 года, Брезеленц, Ганновер — 20 июля 1866 года, Селаска, Италия, близ Лаго-Маджоре) — немецкий математик, механик и физик.
Член Берлинской и Парижской академии наук, Лондонского королевского общества (1859—1860). За свою короткую жизнь (всего десять лет трудов) он преобразовал сразу несколько разделов математики, в том числе математический анализ, комплексный анализ, дифференциальную геометрию, математическую физику и арифметику, внёс вклад в создание топологии. «Мы склонны видеть в Римане, может быть, величайшего математика середины XIX века, непосредственного преемника Гаусса», — отмечал академик П. С. Александров[1].
Биография
Риман был старшим сыном бедного пастора, вторым из шести его детей. Смог начать посещать школу лишь в 14 лет (1840). Мать Римана, Шарлотта Эбелль, умерла от туберкулёза, когда он ещё учился в школе; от этой же болезни умерли две его сестры и, впоследствии, умрёт он сам. Риман всю жизнь был очень привязан к своей семье[2].
Наклонности к математике проявлялись у молодого Римана ещё в детстве, но, уступая желанию отца, в 1846 году он поступил в Гёттингенский университет для изучения филологии, философии и богословия. Однако, увлечённый лекциями Гаусса, юноша принял окончательное решение стать математиком[3].
В 1847 году Риман перешёл в Берлинский университет, где преподавали Дирихле, Якоби и Штейнер. В 1849 году он вернулся в Гёттинген[3], где познакомился с Вильгельмом Вебером, который стал его учителем и близким другом; годом позже приобрёл ещё одного друга — Рихарда Дедекинда.
В 1851 году Риман защитил диссертацию «Основания теории функций комплексной переменной», его научным руководителем был Гаусс, высоко ценивший талант своего ученика. В диссертации впервые было введено понятие, позже получившее известность как риманова поверхность. В 1854—1866 годах Риман работал в Гёттингенском университете[3].

Чтобы претендовать на должность экстраординарного профессора, Риман по уставу должен был выступить перед профессорским составом. Осенью 1853 года Риман прочитал в присутствии Гаусса исторический доклад «О гипотезах, лежащих в основании геометрии», с которого ведёт своё начало риманова геометрия. Доклад, впрочем, не помог — Римана не утвердили. Однако текст выступления был опубликован (хотя и с большим опозданием — в 1868 году), и это стало эпохальным событием для геометрии. Всё же Риман был принят приват-доцентом Гёттингенского университета, где читает курс абелевых функций.
В 1857 году Риман опубликовал классические труды по теории абелевых функций и аналитической теории дифференциальных уравнений и был переведён на должность экстраординарного профессора Гёттингенского университета.
С 1859 года, после смерти Дирихле, Риман — ординарный профессор математики Гёттингенского университета, читает заодно лекции по математической физике (изданы посмертно его учениками). Вместе с Дедекиндом он совершил поездку в Берлинский университет, где общался с Вейерштрассом, Куммером, Кронекером. После чтения там знаменитой работы «О числе простых чисел, не превышающих заданной величины» Риман по рекомендации Вейерштрасса избран членом Берлинской академии наук (1859). Эта работа исследовала распределение простых чисел и свойства ζ-функции (функции Римана). В следующем 1860 году Риман был избран членом Парижской академии наук и Лондонского королевского общества.

В 1862 году Риман женился на Эльзе Кох, подруге покойной сестры. У них родилась дочь Ида. Вскоре после женитьбы Риман простудился и серьёзно заболел. Надеясь укрепить здоровье, Риман с женой в декабре 1862 года уехали в Италию (вначале на год с возвратом в Гёттинген, затем ещё на два года). В 1866 году Риман скончался в Италии от туберкулёза в возрасте неполных 40 лет.
Посмертный сборник трудов Римана, подготовленный Дедекиндом, содержал всего один том. Могила Римана в Италии была заброшена и позже уничтожена при перепланировке кладбища, но надгробная плита уцелела и в наши дни установлена у стены кладбища.
Научная деятельность
Исследования Римана относятся к теории функций комплексного переменного, геометрии, математической и теоретической физике, теории дифференциальных уравнений[3], теории чисел.
Работы по математике
В знаменитом докладе «О гипотезах, лежащих в основании геометрии» (нем. Über die Hypothesen, welche der Geometrie zu Grunde liegen) Риман определил общее понятие n-мерного многообразия и его метрики в виде произвольной положительно определённой квадратичной формы, называемой сейчас римановой метрикой. Далее Риман обобщил гауссову теорию поверхностей на многомерный случай; при этом был впервые введён тензор кривизны и другие фундаментальные понятия римановой геометрии. Существование метрики, по Риману, объясняется либо дискретностью пространства, либо некими физическими силами связи — здесь он предвосхитил общую теорию относительности. Альберт Эйнштейн писал: «Риман первый распространил цепь рассуждений Гаусса на континуумы произвольного числа измерений, он пророчески предвидел физическое значение этого обобщения евклидовой геометрии»[4].
Риман также высказал предположение, что геометрия в микромире может отличаться от трёхмерной евклидовой[5]:
Эмпирические понятия, на которых основывается установление пространственных метрических отношений, — понятия твёрдого тела и светового луча, по-видимому, теряют всякую определённость в бесконечно малом. Поэтому вполне мыслимо, что метрические отношения пространства в бесконечно малом не отвечают геометрическим допущениям; мы действительно должны были бы принять это положение, если бы с его помощью более просто были объяснены наблюдаемые явления.

В другом месте этой же работы Риман указал, что допущения евклидовой геометрии должны быть проверены также и «в сторону неизмеримо большого», то есть в космологических масштабах[6]. Глубокие мысли, содержащиеся в выступлении Римана, ещё долго стимулировали развитие науки.
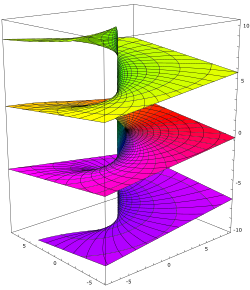
Риман является создателем геометрического направления теории аналитических функций. Он разработал теорию конформных отображений и общую теорию многозначных комплексных функций, построив для них носящие его имя римановы поверхности, на которых эти функции однозначны. Он использовал не только аналитические, но и топологические методы; позднее его труды продолжил Анри Пуанкаре, завершив создание топологии[3].
Труд Римана «Теория абелевых функций» был важным шагом в бурном развитии этого раздела анализа в XIX веке. Риман ввёл понятие рода абелевой функции[англ.], классифицировал их по этому параметру и вывел топологическое соотношение между родом, числом листов и числом точек ветвления функции.
Вслед за Коши Риман рассмотрел формализацию понятия интеграла и ввёл своё определение — интеграл Римана, ставший стандартом в классическом анализе. Развил общую теорию тригонометрических рядов, не сводящихся к рядам Фурье.
В аналитической теории чисел большой резонанс имело исследование Риманом распределения простых чисел. Он дал интегральное представление дзета-функции Римана, исследовал её полюса и нули, выдвинул гипотезу Римана. Вывел приближённую формулу для оценки количества простых чисел через интегральный логарифм.
Работы по механике
Исследования Римана в области механики относятся к изучению динамики течений сжимаемой жидкости (газа) — в частности, сверхзвуковых. Наряду с К. Доплером, Э. Махом, У. Дж. Ранкином и П.-А. Гюгонио Риман стал одним из основоположников классической газовой динамики[7].
Риманом был предложен метод аналитического решения нелинейного уравнения, описывающего одномерное движение сжимаемой жидкости; позже геометрическая разработка данного метода привела к созданию метода характеристик (сам Риман термина «характеристика» и соответствующих геометрических образов не использовал)[8]. Фактически им был создан общий метод для расчёта течений газов в предположении, что данные течения зависят только от двух независимых переменных[9].
В 1860 году Риман нашёл точное общее решение нелинейных уравнений одномерного течения сжимаемого газа (при условии его баротропности); оно представляет собой бегущую плоскую волну конечной амплитуды (простую волну), профиль которой — в отличие от случая волн малой амплитуды — меняет со временем свою форму[10].
Исследуя задачу о распространении малых возмущений при одномерном движении баротропной жидкости, Риман предложил выполнить в уравнениях движения замену зависимых переменных: перейти от переменных [math]\displaystyle{ p }[/math] и [math]\displaystyle{ v }[/math] (давление и скорость) к новым переменным
- [math]\displaystyle{ J_1 = v + \int\frac{\mathrm{d}p}{\rho c}, }[/math]
- [math]\displaystyle{ J_2 = v - \int\frac{\mathrm{d}p}{\rho c} }[/math]
(получивших название инвариантов Римана), в которых уравнения движения принимают особенно простой вид (здесь [math]\displaystyle{ \rho }[/math] — плотность жидкости, [math]\displaystyle{ c }[/math] — скорость звука)[11].
Именно Риману механика обязана понятием об ударных волнах. Явление образования ударных волн в потоке сжимаемого газа впервые было обнаружено не экспериментально, а теоретически — в ходе проводившегося Риманом изучения решений уравнений движения газа (среди которых, как выяснилось, имеются решения с подвижными поверхностями сильного разрыва)[12].
Риман сделал и первую попытку получить условия на поверхности разрыва (то есть соотношения, связывающие скачки физических величин при переходе через данную поверхность). Однако в этом он не преуспел (поскольку фактически исходил из законов сохранения массы, импульса и энтропии, а следовало исходить из законов сохранения массы, импульса и энергии)[13]; правильные соотношения в случае одномерного движения газа были получены Ранкином (1870) и Гюгонио (1887)[7].
Список терминов, связанных с именем Римана
- Геометрия Римана
- Гипотеза Римана
- Дзета-функция Римана
- Инварианты Римана
- Интеграл Римана
- Кратный интеграл Римана
- Производная Римана
- Риманова геометрия
- Риманова поверхность
- Сфера Римана
- Тензор кривизны Римана
- Теорема Римана об отображении
- Теорема Римана об условно сходящихся рядах
- Теорема Римана об устранимой особой точке
- Условия Коши — Римана
Память
В 1964 году Международный астрономический союз присвоил имя Римана кратеру на видимой стороне Луны. В честь Бернхарда Римана 19 октября 1994 года названа малая планета (4167) Riemann, открытая 2 октября 1978 года Л. В. Журавлёвой в Крымской астрофизической обсерватории[14].
Труды на русском языке
- Риман Б. Сочинения. М.-Л.: ОГИЗ. Государственное издательство технико-теоретической литературы, 1948.
- ЧАСТЬ I. Работы Римана по анализу, теории функций и теории чисел (47).
- I. Основы общей теории функций одной комплексной переменной (49).
- II. Теория абелевых функций (88).
- III. Об обращении в нуль 0-функций (139).
- IV. О сходимости бесконечных 0-рядов p-й кратности (151).
- V. Доказательство теоремы о том, что однозначная функция n переменных не может иметь более 2n периодов (155).
- VI. Новые результаты из теории функций, представимых гауссовым рядом F(a, b, y, x) (159).
- VII. Две теоремы общего характера, касающиеся линейных дифференциальных уравнений с алгебраическими коэффициентами (176).
- VIII. О разложении отношения двух гипергеометрических рядов в бесконечную непрерывную дробь (187).
- IX. Об интегралах линейного дифференциального уравнения второго порядка в окрестности точки ветвления (194).
- X. Из лекций по гипергеометрическому ряду (196).
- XI. О числе простых чисел, не превышающих данной величины (216).
- XII. О возможности представления функции посредством тригонометрического ряда (225).
- XIII. Опыт обобщения действия интегрирования и дифференцирования (262).
- ЧАСТЬ II. Работы Римана по геометрии, механике и математической физике (277).
- XIV. О гипотезах, лежащих в основании геометрии (279).
- XV. Фрагменты, относящиеся к Analysis situs (294).
- XVI. О поверхности, имеющей при заданной границе наименьшую площадь (297).
- XVII. Примеры поверхностей наименьшей площади при заданной границе (330).
- XVIII. О движении жидкого однородного эллипсоида (339).
- XIX. О потенциале тора (367).
- XX. Извлечение из письма профессору Энрико Бетти (378).
- XXI. О распространении плоских волн конечной амплитуды (376).
- XXII. Распространение тепла в эллипсоиде (396).
- XXIII. Математическое сочинение, в котором содержится попытка дать ответ на вопрос, предложенный знаменитейшей Парижской Академией, и т. д. (399).
- XXIV. Равновесие электричества на круговых цилиндрах с параллельными осями. Конформное отображение фигур, ограниченных кругами (414).
- XXV. К теории цветных колец Нобили (418).
- XXVI. О законах распределения статического электричества в материальных телах и т. д. (425).
- XXVII. Новая теория остаточного заряда в аппаратах, служащих для накопления электричества (431).
- XXVIII. По поводу электродинамики (443).
- XXIX. О механизме уха (449).
- XXX. Фрагменты философского содержания (461).
- ЧАСТЬ I. Работы Римана по анализу, теории функций и теории чисел (47).
Документальные фильмы
В фильме «BBC. Музыка простых чисел» рассказывается о гипотезе Римана.
Примечания
- ↑ http://new.philos.msu.ru/vestnik/archive/1988/no41988/ Архивная копия от 19 января 2015 на Wayback Machine с. 22
- ↑ Пиньейро, 2015, с. 20, 135.
- ↑ 3,0 3,1 3,2 3,3 3,4 Боголюбов, 1983, с. 412.
- ↑ Эйнштейн А. Сущность теории относительности. — М.: Иностранная литература, 1955. С. 60.
- ↑ Риман Б. Сочинения. М.-Л.: ГИТТЛ, 1948. — С. 291.
- ↑ Хрестоматия по истории математики. Арифметика и алгебра. Теория чисел. Геометрия / Под ред. А. П. Юшкевича. — М.: Просвещение, 1976. — С. 295.
- ↑ 7,0 7,1 Тюлина, 1979, с. 235.
- ↑ Тюлина, 1979, с. 236.
- ↑ Truesdell, 1976, с. 125.
- ↑ Ландау, Лифшиц, 1986, с. 526—529.
- ↑ Ландау, Лифшиц, 1986, с. 547.
- ↑ Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 1. — С. 391—406. — 492 с.
- ↑ Годунов С. К. Элементы механики сплошной среды. — М.: Наука, 1978. — С. 277. — 304 с.
- ↑ M.P.C. 24121 // Циркуляры малых планет = MINOR PLANET CIRCULARS/MINOR PLANETS AND COMETS. — Cambridge, MA, U.S.A.: Центр малых планет, 1994. — Т. 1994 OCT. 19. — С. 119. — 130 с.
Литература
- Боголюбов А. Н. Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.
- Дербишир Дж. Простая одержимость. Бернхард Риман и величайшая нерешённая проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2.
- Математика XIX века / Под ред. А. Н. Колмогорова, А. П. Юшкевича. — М.: Наука, 1978—1987.
- Том 1 Математическая логика. Алгебра. Теория чисел. Теория вероятностей. 1978. (недоступная ссылка)
- Том 2 Геометрия. Теория аналитических функций. 1981. (недоступная ссылка)
- Ландау Л. Д., Лифшиц Е. М. Гидродинамика. 3-е изд. — М.: Наука, 1986. — 736 с. — (Теоретическая физика. Т. VI).
- Монастырский М. И. Бернхард Риман. Топология. Физика. — М.: Янус-К, 1999. — 188 с. — ISBN 5-8037-0025-8.
- Пиньейро Г. Э. Математика переходит границы. Риман. Дифференциальная геометрия // Наука. Величайшие теории. — М.: Де Агостини, 2015. — Вып. 41. — ISSN 2409-0069.
- Тюлина И. А. История и методология механики. — М.: Изд-во Моск. ун-та, 1979. — 282 с.
- Truesdell C. History of Classical Mechanics. Part II, the 19th and 20th Centuries // Die Naturwissenschaften, 63, 3. — 1976. — P. 119—130.
- Персоналии по алфавиту
- Родившиеся в Нижней Саксонии
- Умершие в Пьемонте
- Учёные по алфавиту
- Математики по алфавиту
- Математики Германии
- Математики XIX века
- Механики по алфавиту
- Механики Германии
- Механики XIX века
- Физики по алфавиту
- Физики Германии
- Физики XIX века
- Преподаватели Гёттингенского университета
- Члены Гёттингенской академии наук
- Члены Прусской академии наук
- Члены Баварской академии наук
- Члены-корреспонденты Французской академии наук
- Иностранные члены Лондонского королевского общества
- Умершие от туберкулёза
- Бернхард Риман
- Преподаватели по алфавиту