Обхват (теория графов)
Обхват графа — длина наименьшего цикла, содержащегося в данном графе[1]. Если граф не содержит циклов (то есть является ациклическим графом), его обхват по определению равен бесконечности[2]. Например, 4-цикл (квадрат) имеет обхват 4. Квадратная решётка имеет также обхват 4, а треугольная сетка имеет обхват 3. Граф с обхватом четыре и более не имеет треугольников.
Клетки
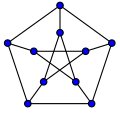
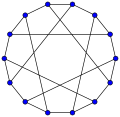
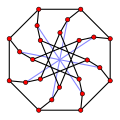
Кубические графы (все вершины имеют степень три) с как можно меньшим обхватом [math]\displaystyle{ g }[/math] известны как [math]\displaystyle{ g }[/math]-клетки (или как (3,[math]\displaystyle{ g }[/math])-клетки). Граф Петерсена — это единственная 5-клетка (наименьший кубический граф с обхватом 5), граф Хивуда — это единственная 6-клетка, граф Макги — это единственная 7-клетка, а граф Татта — Коксетера — это единственная 8-клетка[3]. Может существовать несколько (графов-)клеток для данного обхвата. Например, существует три неизоморфных 10-клетки, каждая с 70 вершинами — 10-клетка Балабана, граф Харриса и граф Харриса — Вонга.
-
Граф Петерсена имеет обхват 5
-
Граф Хивуда имеет обхват 6
-
граф Макги имеет обхват 7
-
Граф Татта — Коксетера (8-клетка Татта) имеет обхват 8
Обхват и раскраска графа
Для любого положительного целого [math]\displaystyle{ k }[/math] существует граф [math]\displaystyle{ G }[/math] с обхватом [math]\displaystyle{ g(G) \ge k }[/math] и хроматическим числом [math]\displaystyle{ \chi(G) \ge k }[/math]. Например, граф Грёча является графом без треугольников и имеет хроматическое число 4, а многократное повторение конструкции Мыцельскиана, используемой для создания графа Грёча, образует графы без треугольников со сколь угодно большим хроматическим числом. Пал Эрдёш доказал эту теорему используя вероятностный метод[4].
План доказательства. Назовём циклы длиной не более [math]\displaystyle{ k }[/math] короткими, а множества с [math]\displaystyle{ |G|/k }[/math] и более вершин — большими. Для доказательства теоремы достаточно найти граф [math]\displaystyle{ G }[/math] без коротких циклов и больших независимых множеств вершин. Тогда множества цветов в раскраске не будут большими, и, как следствие, для раскраски потребуется [math]\displaystyle{ k }[/math] цветов.
Чтобы найти такой граф, будем фиксировать вероятность выбора [math]\displaystyle{ p }[/math] равной [math]\displaystyle{ n^{\epsilon - 1} }[/math]. При малых [math]\displaystyle{ \epsilon }[/math] в [math]\displaystyle{ G }[/math] возникает лишь малое число коротких циклов. Если теперь удалить по вершине из каждого такого цикла, полученный граф [math]\displaystyle{ H }[/math] не будет иметь коротких циклов, а его число независимости будет не меньше, чем у графа [math]\displaystyle{ G }[/math][1].
Близкие концепции
Нечётный обхват и чётный обхват графа — это длины наименьшего нечётного цикла и чётного цикла соответственно.
Окружность графа — это длина наибольшего по длине цикла, а не наименьшего.
Размышления о длине наименьшего нетривиального цикла можно рассматривать как обобщение 1-систолы или большей систолы в систолической геометрии.
Примечания
- ↑ Перейти обратно: 1,0 1,1 Рейнгард Дистель. Теория графов. — Новосибирск: Издательство института математики, 2002.
- ↑ Girth -- Wolfram MathWorld.
- ↑ Andries E. Brouwer. Cages. Электронное приложение к книге Distance-Regular Graphs (Brouwer, Cohen, Neumaier 1989, Springer-Verlag).
- ↑ Paul Erdős. Graph theory and probability // Canadian Journal of Mathematics. — 1959. — Т. 11. — С. 34—38. — doi:10.4153/CJM-1959-003-9.
Для улучшения этой статьи желательно: |