Минор графа

Минор в теории графов — граф [math]\displaystyle{ H }[/math] для заданного графа [math]\displaystyle{ G }[/math], который может быть образован из [math]\displaystyle{ G }[/math] удалением рёбер и вершин и стягиванием рёбер.

Теория миноров графов началась с теоремы Вагнера, гласящей, что граф планарен в том и только в том случае, когда в его миноры не входят ни полный граф K₅, ни полный двудольный граф K_3,3. Из теоремы Робертсона — Сеймура следует, что аналоги характеризации запрещёнными минорами существуют для любого свойства графов, которые сохраняются при удалениях и стягивании рёбер.

Для любого графа H можно проверить, является ли H минором входного графа G за полиномиальное время. Вместе с характеризацией запрещёнными минорами из этого следует, что любое свойство графа, сохраняющееся при удалениях и стягиваниях, может быть распознано за полиномиальное время.

Среди других результатов и гипотез, использующих миноры графов, находятся теорема о структуре графа, согласно которой графы, не содержащие H в качестве минора, могут быть образованы склеиванием более простых частей, и гипотеза Хадвигера, связывающая невозможность раскраски графа с существованием большого полного графа в качестве его минора. Важными вариантами миноров графов являются топологические миноры и погружённые миноры.

Определения

Стягивание ребра — это операция, которая удаляет ребро из графа, а концы ребра сливаются в одну вершину. Неориентированный граф H является минором другого неориентированного графа G, если граф, изоморфный H, может быть получен из G стягиванием рёбер, удалением некоторых рёбер и удалением некоторых изолированных вершин. Порядок, в котором производится стягивания и удаления в G, не влияют на результирующий граф H.

Миноры графов часто изучаются в более общем контексте миноров матроидов. В этом контексте обычно полагается, что графы связны, могут иметь петли и multiple edge (то есть, рассматриваются мультиграфы, а не простые графы). Стягивание петли и удаление разрезающего ребра запрещены. При таком подходе удаление ребра оставляет ранг графа неизменным, а стягивание ребра всегда уменьшает ранг на единицу.

В других контекстах (как, например, при изучении псевдолесов) имеет смысл разрешить удаление разрезающих рёбер и позволить графам быть несвязными, но при этом имеет смысл запретить мультиграфы. В таком варианте теории миноров графов граф всегда упрощается после любого стягивания ребра для исключения петель и кратных рёбер

Пример

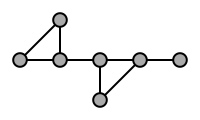
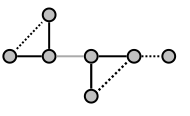
В следующем примере граф H является минором графа G:

H.

G.

Следующий рисунок иллюстрирует это. Сначала строим подграф графа G путём удаления пунктирных рёбер (и возникающую изолированную вершину), а затем стягиваем серое ребро (объединяя две вершины, которые ребро соединяет):

Основные результаты и гипотезы

Можно легко проверить, что отношение миноров графов образует частичный порядок на классе изоморфизмов неориентированных графов — отношение транзитивно (минор минора графа G является сам минором G) и графы G и H могут быть минорами друг друга если они изоморфны, поскольку любая нетривиальная операция с минором удаляет рёбра или вершины. Глубокий результат Нейла Робертсона и Пола Сеймура утверждает, что этот частичный порядок является, на самом деле, вполне квазиупорядоченным — если задан бесконечный список G₁, G₂,… конечных графов, всегда существуют два индекса i < j, такие что G_i является минором графа G_j. Эквивалентная формулировка утверждения — любое множество графов может иметь лишь конечное число минимальных элементов по минорному отношению. Этот результат доказывает гипотезу, до этого известную как гипотеза Вагнера. Вагнер высказал гипотезу много раньше, но опубликовал её лишь в 1970.

По ходу доказательства Сеймур и Робертсон также доказали теорему о структуре графа, в которой они определили для любого фиксированного графа H грубую структуру любого графа, который не содержит H в качестве минора. Утверждение теоремы длинно и запутано, но, вкратце, теорема устанавливает, что такой граф должен иметь структуру суммы по кликам меньших графов, которые получаются небольшой модификацией графов, вложенных в поверхности ограниченного рода. Таким образом, их теория устанавливает фундаментальную связь между минорами графа и топологическими вложениями графов.

Для любого графа H простые свободные от миноров H графы должны быть редкими, что означает, что число рёбер меньше некоторой константы, умноженной на число вершин. Конкретнее, если H имеет h вершин, то простой n-вершинный свободный от H-миноров граф может иметь не более [math]\displaystyle{ \scriptstyle O(nh\sqrt{\log h}) }[/math] рёбер, а некоторые свободные от K_h миноров графы имеют по меньшей мере такое число рёбер. Так, если H имеет h вершин, то свободные от H-миноров графы имеют среднюю степень [math]\displaystyle{ \scriptstyle O(h \sqrt{\log h}) }[/math] и, кроме того, вырожденность [math]\displaystyle{ \scriptstyle O(h \sqrt{\log h}) }[/math]. Вдобавок, свободные от H-миноров графы имеют теорему о разбиении, подобную теореме о разбиении в планарном графе — для любого фиксированного H, и любого n-вершинного свободного от H-миноров графа G можно найти подмножество вершин размером [math]\displaystyle{ \scriptstyle O(\sqrt{n}) }[/math], удаление которого делит граф G на два (возможно несвязных) подграфа с максимум 2n/3 вершинами в каждом. Даже более строго, для любого фиксированного H свободные от H-миноров графы имеют древесную ширину [math]\displaystyle{ \scriptstyle O(\sqrt{n}) }[/math].

Гипотеза Хадвигера делает предположение, что если граф G не содержит минор, изоморфный полному графу с k вершинами, то граф G имеет правильную раскраску в k − 1 цветов. Случай k = 5 является переформулировкой проблемы четырёх красок. Гипотеза Хадвигера доказана для k ≤ 6 , но не в общем виде. Болобас, Катлин и Эрдёш назвали задачу «одной из глубочайших нерешённых задач теории графов». Другой результат, связывающий теорему четырёх красок с минорами графа — это теорема о снарках, о доказательстве которой объявили Робертсон, Сандерс, Сеймур и Томас. Теорема является усилением теоремы четырёх красок и была высказана (как гипотеза) Таттом и она утверждает, что любой 3-регулярный граф без мостов, для рёберной раскраски которого требуется четыре цвета, должен содержать граф Петерсена в качестве минора.

Семейства графов, замкнутые по минорам

Подробнее по теме «семейства минорно замкнутых графов» см. Теорема Робертсона — Сеймура

Многие семейства графов обладают свойством, что любой минор графа из F также входит в F. В этом случае говорят, что класс графов минорно замкнут. Например, для любого планарного графа или вложения графа в фиксированную топологическую поверхность ни удаление рёбер, ни стягивание рёбер не может увеличить род вложения. Таким образом, планарные графы и графы, вложимые в любую фиксированную поверхность, образуют минорно замкнутые семейства.

Если F является минорно замкнутым семейством, то (ввиду свойства вполне квазиупорядоченности миноров) среди графов, не принадлежащих F, существует конечное множество X минорно минимальных графов. Эти графы являются запрещёнными минорами для F — граф принадлежит множеству F тогда и только тогда, когда он не содержит в качестве миноров любой граф из X. Таким образом, любое минорно замкнутое семейство F может быть охарактеризовано как семейство свободных от миноров из X графов для некоторого конечного множества X запрещённых миноров.

Хорошо известным примером характеризации такого типа является Теорема Вагнера, характеризующая планарные графы как графы, не имеющие ни K₅, ни K_3,3 в качестве миноров .

В некоторых случаях свойства графов в минорно замкнутом семействе может быть тесно связана со свойствами исключённых миноров. Например, минорно замкнутое семейство графов F имеет ограниченную путевую тогда и только тогда, когда запрещённые семейство семейства включает лес , F имеет ограниченную глубину дерева тогда и только тогда, когда запрещённые миноры включают разъединённое объединение путей, F имеет ограниченную древесную ширину тогда и только тогда, когда его запрещённые миноры включают планарный граф, и F имеет ограниченную локальную древесную ширину (функциональную связь между диаметром и древесной шириной) тогда и только тогда, когда его запрещённые миноры включают верхушечный граф (граф, который становится планарным при удалении одной вершины). Если H может быть нарисован на плоскости с единственным пересечением (то есть, число пересечений графа равно единице), то для свободных от H-миноров графов верна теорема об упрощённой структуре, по которой такие графы представляют собой кликовую сумму планарных графов и графов с ограниченной древесной шириной. Например, как K₅, так и K_3,3 имеют число пересечений, равное единице, и как показал Вагнер, свободные от K₅ графы — это в точности 3-кликовые суммы планарных графов и восьмивершинного графа Вагнера, в то время как свободные от K_3,3 графы — это в точности 2-кликовые суммы планарных графов и K₅.

Вариации

Топологические миноры

Граф H называется топологическим минором графа G, если граф подразбиений графа H изоморфен подграфу графа G . Легко видеть, что любой топологический минор является минором (в обычном смысле). Обратное, однако, в общем случае неверно (например, полный граф K₅ в графе Петерсена является минором, но не является топологическим минором), но выполняется для графа с максимальной степенью, не превосходящей трёх.

Отношения топологических миноров не является вполне квазиупорядоченным на множестве конечных графов и потому результат Робертсона и Сеймура неприменим к топологическим минорам. Однако легко построить характеризации конечными запрещёнными топологическими минорами из характеризации конечными запрещёнными минорами.

Погружённый минор

Операция с графом, называемая подъёмом, является центральным понятием в концепции погружения. Подъём является операцией со смежными рёбрами. Если заданы три вершины v, u и w, где (v, u) и (u, w) — ребра графа, подъём vuw, или, эквивалентно, (v, u), (u, w) — это операция, которая удаляет два ребра (v, u) и (u, w) и добавляет ребро (v, w). В случае, когда ребро (v, w) уже присутствует, v и w будут соединены ещё одним ребром, а поэтому операция является существенно операцией с мультиграфами.

В случае, когда граф H может быть получен из графа G путём последовательности операций подъёма (над G) а затем нахождения изоморфного подграфа, мы говорим, что H является погружённым минором графа G.

Существует другой способ определения погружённых миноров, который эквивалентен операции подъёма. Мы говорим, что H является погружённым минором графа G, если существует инъективное отображение из вершин H в вершины G, при котором образы смежных элементов H соединены в G путями, не имеющими общих рёбер.

Отношение погружённых миноров является вполне квазиупорядоченным на множестве конечных графов, а потому результаты Роебртсона и Сеймура применимы к погружённым минорам. Более того, это означает, что любое семейство, замкнутое по погружённым минорам, характеризуется конечным семейством запрещённых вложенных миноров.

В области визуализация графов погружённые миноры появляются как планаризации непланарных графов — из рисунка графа на плоскости с пересечениями может быть образован погружённый минор путём замены каждой точки пересечения новой вершиной и разбиения каждого пересечённого ребра на путь. Это позволяет распространить методы рисования планарных графов на непланарные графы .

Неглубокие миноры

Неглубокий минор графа G — это минор, в котором рёбра графа G, стянутые для получения минора, образуют непересекающиеся подграфы малого диаметра. Неглубокие миноры образуют как бы мост между минорами графа и подграфами в том смысле, что неглубокие миноры с высокой глубиной совпадают с обычными типами миноров, в то время как неглубокие миноры с нулевой глубиной — это в точности подграфы. Они также позволяют распространить теорию миноров графа на классы графов, такие как 1-планарные графы, которые не замкнуты по взятию миноров.

Алгоритмы

Задача разрешимости, содержится ли граф H в графе G в качестве минора является, в общем случае, NP-полной. Например, если H является циклом с тем же числом вершин, что и у G, то H является минором графа G тогда и только тогда, когда G содержит гамильтонов граф. Однако, если G является входным, а H фиксирован, задача может быть решена за полиномиальное время. Конкретнее, время работы проверки, является ли H минором графа G в этом случае равно O(n³), где n — число вершин в G, а O большое прячет константу, которая зависит суперэкспоненциально от H. Вследствие результата о минорах графа этот алгоритм улучшается до O(n²). Таким образом, при применении алгоритма с полиномиальным временем работы для проверки, содержит ли заданный граф какой-либо из запрещённых миноров, можно распознать члены любого минорно замкнутого семейства за полиномиальное время. Однако, чтобы применять этот результат конструктивно, необходимо знать запрещённые миноры семейства графов.

Ссылки

• Weisstein, Eric W. Graph Minor (англ.) на сайте Wolfram MathWorld.