Полное усечение (геометрия)

Полностью усечённый куб является кубооктаэдром – рёбра сводятся к вершинам, а вершины расширяются до новых граней

Дважды полностью усечённый куб является октаэдром – грани уменьшаются до точек и новые грани образуются вместо вершин.

Полностью усечённые кубические соты – рёбра уменьшаются до вершин, а вершины превращаются в новые ячейки.

В евклидовой геометрии спрямление или полное усечение — это процесс усечения многогранника путём пометки середины всех его рёбер и отсечения всех вершин вплоть до этих точек . Получающийся многогранник будет ограничен фасетами (гранями размерности n-1, в трёхмерном пространстве это многоугольники) вершинных фигур и усечёнными фасетами исходного многогранника. Операции спрямления даётся однобуквенный символ r. Так, например, r{4,3} — спрямлённый куб, т.е. кубооктаэдр.

Конвей для этой операции использует обозначение ambo. В теории графов эта операция создаёт срединный граф.

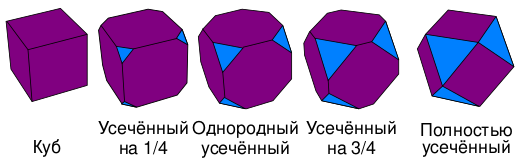
Пример спрямления как финальной стадии усечения ребра

Полное усечение является финальной стадией процесса усечения. На рисунке показаны четыре стадии непрерывного процесса усечения от правильного куба до полностью усечённого состояния:

Более высокие степени полного усечения

Более высокие степени полного усечения могут быть осуществлены на правильных многогранниках более высоких размерностей. Наивысшая степень полного усечения создаёт двойственный многогранник. Спрямление усекает рёбра до точек. Двойное спрямление усекает (двумерные) грани до точек. В более высоких размерностях тройное спрямление усекает ячейки (трёхмерные грани) до точек, и так далее.

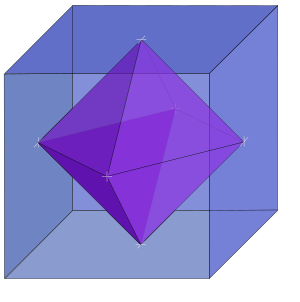
Пример двойного спрямления как финальной стадии усечения граней

Последовательность на рисунке показывает двойное усечение куба как конечную стадию процесса от куба к двойственному октаэдру, при котором исходная грань усекается до точки:

Для многоугольников

Двойственный многоугольник — это то же самое, что и полностью усечённая его форма. Новые вершины располагаются в серединах сторон исходного многоугольника.

Для многогранников и плоских мозаик

Дополнительные сведения: Квазиправильный многогранник

Любой правильный многогранник и его двойственный имеют один и тот же полностью усечённый многогранник. (Это не так для многогранников в пространствах размерности 4 и более.)

Полностью усечённый многогранник может быть получен как пересечение исходного правильного многогранника с подходящим образом масштабированной концентрической версии двойственного. По этой причине их имена строятся как комбинации имени исходного многогранника и его двойственного:

1. Полностью усечённый тетраэдр, двойственным которому является тетраэдр, носит имя тетратетраэдр, более известный как октаэдр.
2. Полностью усечённый октаэдр, двойственным которому является куб, носит имя кубооктаэдр.
3. Полностью усечённый икосаэдр, двойственным которому является додекаэдр, носит имя икосододекаэдр.
4. Полностью усечённый квадратный паркет — это квадратный паркет.
5. Полностью усечённый треугольный паркет, двойственным которому является шестиугольный паркет, носит имя тришестиугольный паркет.

Примеры

Семейство	Родитель	Полное усечение	Двойственный
[p,q]
[3,3]	Тетраэдр	Октаэдр	Тетраэдр
[4,3]	Куб	Кубооктаэдр	Октаэдр
[5,3]	Додекаэдр	Икосододекаэдр	Икосаэдр
[6,3]	Шестиугольная мозаика	Тришестиугольная мозаика	Треугольная мозаика
[7,3]	Семиугольная мозаика третьего порядка	Трисемиугольная мозаика	Треугольная мозаика седьмого порядка
[4,4]	Квадратная мозаика	Квадратная мозаика	Квадратная мозаика
[5,4]	Пятиугольная мозаика четвёртого порядка	Квадратно-пятиугольная мозаика	Квадратная мозаика пятого порядка

Для неправильных многогранников

Если многогранник не является правильным, середины рёбер, окружающих вершину, могут не лежать в одной плоскости. Однако некая форма полного усечения остаётся возможной и в этом случае — любой многогранник имеет полиэдральный граф, как 1-скелет (многогранника), и из этого графа можно образовать срединный граф путём помещения вершин в середины рёбер исходного графа и соединения двух новых вершин ребром, если они принадлежат последовательным рёбрам вдоль общей грани. Получившийся срединный граф остаётся полиэдральным, так что по теореме Штайница его можно представить в виде многогранника.

Эквивалент нотации Конвея для полного усечения — это ambo, обозначаемый буквой a. Применяя дважды aa, (спрямление после спрямления) — это конвеевская операция расширения, e, которая является той же операцией, что и операция скашивания Джонсона, t_0,2 для правильных многогранников и мозаик.

Для 4-мерных многогранников и 3-мерных мозаик

Любой выпуклый правильный 4-мерный многогранник имеет форму полного усечения, как однородный 4-мерный многогранник.

Правильный 4-мерный многогранник {p,q,r} имеет ячейки {p,q}. Его полное усечение даст два типа ячеек — полностью усечённые {p,q} многогранники, оставшиеся от исходных ячеек, и {q,r} многогранники как новые ячейки, образованные на местах отсечённых вершин.

Однако усечение {p,q,r} не совпадает с усечением {r,q,p}. Дальнейшее усечение, называемое двойным полным усечением, симметрично относительно 4-мерного многогранника и его двойственного. Смотрите Однородный 4-мерный многогранник.

Примеры

Семейство	Родитель	Полное усечение	Двойное полное усечение (Усечение двойственного)	Тройное полное усечение (Двойственный)
[p,q,r]
[3,3,3]	Пятиячейник	Полностью усечённый пятиячейник	Полностью усечённый пятиячейник	Пятиячейник
[4,3,3]	тессеракт	Полностью усечённый тессеракт	Полностью усечённый шестнадцатиячейник (двадцатичетырёхячейник)	Шестнадцатиячейник
[3,4,3]	Двадцатичетырёхячейник	Полностью усечённый 24-ячейник	Полностью усечённый 24-ячейник	Двадцатичетырёхячейник
[5,3,3]	Стодвадцатиячейник	Полностью усечённый 120-ячейник	Полностью усечённый 600-ячейник	Шестисотячейник
[4,3,4]	Кубические соты	Полностью усечённые кубические соты	Полностью усечённые кубические соты	Кубические соты
[5,3,4]	Додекаэдральные соты 4-го порядка	Полностью усечённые додекаэдральные соты 4-го порядка	Полностью усечённые кубические соты 5-го порядка	Кубические соты 5-го порядка

Степени спрямления

Первое полное усечение усекает рёбра до точек. Если многогранник является правильным, эта форма представляется расширенным символом Шлефли t₁{p,q,...} или r{p,q,...}.

Второе полное усечение, или двойное спрямление, усекает грани до точек. Если многогранник правильный, двойное полное усечение обозначается t₂{p,q,...} или 2r{p,q,...}. Для 3-мерных многогранников двойное полное усечение даёт двойственный многогранник.

Более высокие степени полного усечения можно построить для многогранников в пространствах размерности 4 и выше. В общем случае, уровень полного усечения n отсекает n-мерные грани до точек.

Если многогранник в n-мерном пространстве полностью усечён до степени (n-1), его фасеты (грани размерности n-1) усекаются до точки и он становится двойственным исходному.

Обозначения и фасеты

Существует три различных эквивалентных обозначения для каждой степени полного усечения. Таблицы ниже показывают имена по размерности и два типа фасет для каждого.

Правильные многоугольники

Фасеты — это рёбра, представленные как {2}.

название {p}	Диаграмма Коксетера	t-запись Символ Шлефли	Вертикальный символ Шлефли
			Название	Фасет-1	Фасет-2
Родитель		t0{p}	{p}	{2}
Полностью усечённый		t1{p}	{p}		{2}

Правильные 3-мерные однородные многогранники и мозаики

Фасеты являются правильными многоугольниками.

Название {p,q}	Диаграмма Коксетера	t-запись Символ Шлефли	Вертикальный символ Шлефли
			Название	Фасет-1	Фасет-2
Родитель		t0{p,q}	{p,q}	{p}
Полностью усечённый		t1{p,q}	[math]\displaystyle{ \begin{Bmatrix} p \\ q \end{Bmatrix} }[/math] = r{p,q}	{p}	{q}
Дважды усечённый		t2{p,q}	{q,p}		{q}

Правильные однородные 4-мерные многогранники и соты

Фасеты — правильные или полностью усечённые многогранники.

название {p,q,r}	Диаграмма Коксетера	t-запись Символ Шлефли	Расширенный символ Шлефли
			Название	Фасет-1	Фасет -2
Родитель		t0{p,q,r}	{p,q,r}	{p,q}
Rectified		t1{p,q,r}	[math]\displaystyle{ \begin{Bmatrix} p \ \ \\ q , r \end{Bmatrix} }[/math] = r{p,q,r}	[math]\displaystyle{ \begin{Bmatrix} p \\ q \end{Bmatrix} }[/math] = r{p,q}	{q,r}
Дважды полностью усечённый (Полностью усечённый двойственный)		t2{p,q,r}	[math]\displaystyle{ \begin{Bmatrix} q , p \\ r \ \ \end{Bmatrix} }[/math] = r{r,q,p}	{q,r}	[math]\displaystyle{ \begin{Bmatrix} q \\ r \end{Bmatrix} }[/math] = r{q,r}
Трихды полностью усечённый (Двойственный)		t3{p,q,r}	{r,q,p}		{r,q}

Правильные многогранники в 5-мерном пространстве и 4-мерные соты

Фасеты являются правильными или полностью усечёнными четырёхмерными многогранниками.

Название {p,q,r,s}	Диаграмма Коксетера	t-запись символа Шлефли	Расширенный символ Шлефли
			Название	Фасет-1	Фасет -2
Родитель		t0{p,q,r,s}	{p,q,r,s}	{p,q,r}
Полностью усечённый		t1{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} p \ \ \ \ \ \\ q , r , s \end{Bmatrix} }[/math] = r{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} p \ \ \\ q , r \end{Bmatrix} }[/math] = r{p,q,r}	{q,r,s}
Дважды полностью усечённый (Дважды полностью усечённый двойственный)		t2{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} q , p \\ r , s \end{Bmatrix} }[/math] = 2r{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} q , p \\ r \ \ \end{Bmatrix} }[/math] = r{r,q,p}	[math]\displaystyle{ \begin{Bmatrix} q \ \ \\ r , s \end{Bmatrix} }[/math] = r{q,r,s}
Трижды полностью усечённый (Полностью усечённый двойственный)		t3{p,q,r,s}	[math]\displaystyle{ \begin{Bmatrix} r , q , p \\ s \ \ \ \ \ \end{Bmatrix} }[/math] = r{s,r,q,p}	{r,q,p}	[math]\displaystyle{ \begin{Bmatrix} r , q \\ s \ \ \end{Bmatrix} }[/math] = r{s,r,q}
Четырежды полностью усечённый (двойственный)		t4{p,q,r,s}	{s,r,q,p}		{s,r,q}

См. также

• Двойственный многогранник
• Квазиправильный многогранник
• Список правильных многогранников
• Усечение (геометрия)
• Нотация Конвея для многогранников

Ссылки

• Джордж Ольшевски Rectification на Glossary for Hyperspace.