Функция Минковского

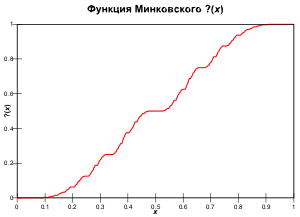
Функция «вопросительный знак» Минковского — построенная Германом Минковским монотонная сингулярная функция [math]\displaystyle{ ?(x) }[/math] на отрезке [math]\displaystyle{ [0, 1] }[/math], обладающая рядом замечательных свойств. Так, она взаимно-однозначно и с сохранением порядка переводит квадратичные иррациональности (то есть, числа вида [math]\displaystyle{ a + \sqrt{b}, }[/math] где [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] рациональные) на отрезке [math]\displaystyle{ [0, 1] }[/math] в рациональные числа на том же отрезке, а рациональные числа — в двоично-рациональные. Она связана с рядами Фарея, цепными дробями, и дробно-линейными преобразованиями, а её график обладает рядом интересных симметрий.

Построение

Функция Минковского может быть задана несколькими эквивалентными способами: через ряды Фарея, через цепные дроби, и построением графика с помощью последовательных итераций.

Задание с помощью дерева Штерна — Броко

В концах отрезка функция Минковского задаётся как [math]\displaystyle{ ?(0) = 0 }[/math] и [math]\displaystyle{ ?(1) = 1 }[/math]. После этого для любых двух рациональных чисел [math]\displaystyle{ \frac{a}{b} }[/math] и [math]\displaystyle{ \frac{c}{d} }[/math], для которых [math]\displaystyle{ ad - bc = 1 }[/math] — иными словами, для любых двух последовательных в каком-либо из рядов Фарея, — функция в их медианте [math]\displaystyle{ \frac{a + c}{b + d} }[/math] определяется как среднее арифметическое значений в этих точках:

[math]\displaystyle{ ?\left(\frac{a + c}{b + d}\right) = \frac{1}{2} \left[?\left(\frac{a}{b}\right) + {}?\left(\frac{c}{d}\right)\right]. }[/math]

Так

[math]\displaystyle{ ?\left(\frac{1}{2}\right) = \frac{?(0) + {}?(1)}{2} = \frac{1}{2}, }[/math]

[math]\displaystyle{ ?\left(\frac{1}{3}\right) = \frac{?(0) + {}?(1/2)}{2} = \frac{1}{4}, }[/math]

[math]\displaystyle{ ?\left(\frac{2}{3}\right) = \frac{?(1/2) + {}?(1)}{2} = \frac{3}{4} }[/math]

и так далее.

Поскольку последовательности

[math]\displaystyle{ \frac{0}{1}, \frac{1}{1}, }[/math]

[math]\displaystyle{ \frac{0}{1}, \frac{1}{2}, \frac{1}{1}, }[/math]

[math]\displaystyle{ \frac{0}{1}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{1}{1}, }[/math]

в которых следующая получается из предыдущей дописыванием между каждыми соседними её элементами их медианты, перечисляют в объединении все рациональные числа отрезка [math]\displaystyle{ [0, 1] }[/math] (см. дерево Штерна — Броко), такая итеративная процедура задаёт функцию Минковского во всех рациональных точках [math]\displaystyle{ [0, 1] }[/math]. Более того, как несложно видеть, множеством её значений в этих точках оказываются в точности все двоично-рациональные числа [math]\displaystyle{ [0, 1] }[/math] — иными словами, плотное в [math]\displaystyle{ [0, 1] }[/math] множество. Поэтому построенная функция по монотонности однозначно продолжается до непрерывной функции [math]\displaystyle{ ? \colon [0, 1] \to [0, 1] }[/math], и это и есть функция Минковского.

Задание с помощью цепной дроби

Функция Минковского, в определённом смысле, преобразует разложение в цепную дробь в представление в двоичной системе счисления. А именно, точку [math]\displaystyle{ x \in [0, 1] }[/math], раскладывающуюся в цепную дробь как [math]\displaystyle{ x = [0; a_1, a_2, \ldots] }[/math], функция Минковского переводит в

[math]\displaystyle{ ?(x) = \sum_{k=1}^\infty \frac{(-1)^{k-1}}{2^{a_1 + \ldots + a_k - 1}}. }[/math]

Иными словами, точка

[math]\displaystyle{ x = \frac{1}{a_1 + \dfrac{1}{a_2 + \dfrac{1}{a_3 + \ldots}}} }[/math]

переходит в точку

[math]\displaystyle{ ?(x) = 0{,}\underbrace{0 \ldots 0}_{a_1-1}\underbrace{1 \ldots 1}_{a_2}\underbrace{0 \ldots 0}_{a_3}\underbrace{1 \ldots 1}_{a_4}\ldots_{(2)}. }[/math]

Самоподобие

Пусть точка [math]\displaystyle{ x \in [0, 1] }[/math] задаётся цепной дробью [math]\displaystyle{ x = [0; a_1, a_2, \ldots] }[/math]. Тогда увеличение [math]\displaystyle{ a_1 }[/math] на единицу, то есть, переход к [math]\displaystyle{ y = [0; a_1 + 1, a_2, \ldots] }[/math] задаётся отображением

[math]\displaystyle{ f \colon x \mapsto y = \frac{1}{1 + \dfrac{1}{x}} = \frac{x}{1 + x}, }[/math]

а функция Минковского после такого преобразования делится (как это следует из её задания через цепную дробь аргумента) пополам:

[math]\displaystyle{ ?\left(\frac{x}{1 + x}\right) = \frac{?(x)}{2}.\qquad(1) }[/math]

С другой стороны, из симметрии относительно [math]\displaystyle{ 1/2 }[/math] медиантной конструкции легко видеть, что

[math]\displaystyle{ ?(1 - x) = 1 - {}?(x).\qquad(2) }[/math]

Сопрягая (1) с помощью (2), видим, что под действием отображения [math]\displaystyle{ g(x) = 1 - f(1 - x) = 1 - \frac{1 - x}{2 - x} = \frac{1}{2 - x} }[/math] функция Минковского преобразуется как

[math]\displaystyle{ ?\left(\frac{1}{2 - x}\right) = \frac{1 + {}?(x)}{2}. }[/math]

Поэтому график функции Минковского переводится в себя каждым из преобразований

[math]\displaystyle{ F(x, t) = \left(\frac{x}{1 + x}, \frac{t}{2}\right), \quad G(x, t) = \left(\frac{1}{2 - x}, \frac{1 + t}{2}\right).\qquad(3) }[/math]

Более того, объединение их образов — это в точности весь исходный график, поскольку образ [math]\displaystyle{ F }[/math] — это часть графика над отрезком [math]\displaystyle{ [0, 1/2] }[/math], а образ [math]\displaystyle{ G }[/math] — график над отрезком [math]\displaystyle{ [1/2, 1] }[/math].

Построение графика как фрактала

График функции Минковского может быть построен как предельное множество для системы итерируемых функций^[англ.]. А именно, отображения [math]\displaystyle{ F }[/math] и [math]\displaystyle{ G }[/math], заданные формулами (3), сохраняют график функции Минковского и переводят единичный квадрат внутрь себя. Поэтому последовательность множеств [math]\displaystyle{ X_n }[/math], определённая рекурсивно соотношениями

[math]\displaystyle{ X_0 = [0, 1] \times [0, 1], \quad X_{n+1} = F(X_n) \cup G(X_n), }[/math]

есть убывающая по вложению последовательность множеств, причём график [math]\displaystyle{ \Gamma = \big\{\big(x, ?(x)\big) \mid x \in [0, 1]\big\} }[/math] функции Минковского содержится в любом из них.

Несложно увидеть, что [math]\displaystyle{ X_n }[/math] является объединением прямоугольников высоты [math]\displaystyle{ 1/2^n }[/math], поэтому предельное множество

[math]\displaystyle{ X_\infty = \bigcap_n X_n }[/math]

является графиком некоторой функции. Поскольку [math]\displaystyle{ \Gamma \subset X_\infty }[/math], то они совпадают. Поэтому график функции Минковского это предельное множество системы итерируемых функций

[math]\displaystyle{ F, G : [0, 1]^2 \to [0, 1]^2. }[/math]

Свойства

Функция Минковского сингулярна, то есть почти всюду (за исключением множества меры 0) производная [math]\displaystyle{ ?'(x) = 0 }[/math]. В точках множества меры 0 существует обобщённая производная, [math]\displaystyle{ ?'(x) = +\infty }[/math]. Тем самым, мера на [math]\displaystyle{ [0, 1] }[/math], функцией распределения которой является функция Минковского (продолженная нулём на отрицательные числа и единицей на числа, большие единицы), сингулярна.
Функция Минковского взаимно однозначно переводит рациональные числа на отрезке [math]\displaystyle{ [0, 1] }[/math] в двоично-рациональные числа на том же отрезке.
Функция Минковского взаимно однозначно переводит квадратичные иррациональности на отрезке [math]\displaystyle{ [0, 1] }[/math] в рациональные числа на том же отрезке. Действительно, число [math]\displaystyle{ x }[/math] является квадратичной иррациональностью тогда и только тогда, когда его разложение в цепную дробь, начиная с некоторого момента, периодично; с другой стороны, эта периодичность равносильна периодичности двоичной записи образа — иными словами, рациональности [math]\displaystyle{ ?(x) }[/math].
График функции Минковского переводится в себя отображениями [math]\displaystyle{ F }[/math] и [math]\displaystyle{ G }[/math], заданными (3), а, следовательно, и их композициями.

Литература

Minkowski H. Verhandlungen des III. internationalen Mathematiker-Kongresses in Heidelberg. — Berlin, 1904.
Denjoy A. Sur une fonction réelle de Minkowski. — Journal de Mathématiques Pures et Appliquées. — 1938. — 17. — pp. 105—151.
Conley, R. M. (2003), A Survey of the Minkowski ?(x) Function, Masters thesis, West Virginia University , ссылка.
Conway, J. H. (2000), Contorted fractions, On Numbers and Games (2nd ed.), Wellesley, MA: A K Peters, с. 82—86 .
Кириллов А. А. Повесть о двух фракталах. — М.: МЦНМО, 2009.

См. также

Канторова лестница

Ссылки

Weisstein, Eric W. Minkowski's Question Mark Function (англ.) на сайте Wolfram MathWorld.