Линейное уравнение

Линейное уравнение — это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна 1. Линейное уравнение можно представить:

в общей форме: [math]\displaystyle{ a_1x_1 + a_2x_2 + \dots + a_nx_n + b = 0 }[/math];
в канонической форме: [math]\displaystyle{ a_1x_1 + a_2x_2 + \dots + a_nx_n = -b }[/math],

где [math]\displaystyle{ x_1, \ldots, x_n }[/math] — это переменные (или неизвестные) величины (также известные как корни линейного уравнения), а [math]\displaystyle{ b, a_1, \ldots, a_n }[/math] — постоянные или коэффициенты, которые являются действительными числами. Коэффициенты могут квалифицироваться как параметры при уравнении и могут быть любыми выражениями при условии, что сами по себе не содержат переменных. Чтобы уравнение имело смысл, коэффициенты [math]\displaystyle{ a_1, \ldots, a_n }[/math] не должны равняться нулю. Также линейное уравнение можно получить, если приравнять линейный многочлен к нулю над некоторым полем, откуда для многочлена берутся коэффициенты.

Решение уравнения — это нахождение таких значений переменных, которые при подстановке дали бы верное равенство. Если переменная всего одна, то для линейного уравнения существует только одно решение (при условии, что [math]\displaystyle{ a_1\ne 0 }[/math]). Часто «линейным уравнением» называют именно подобные уравнения с одной «неизвестной». Если переменных две, то любое решение может быть проиллюстрировано и проверено с помощью прямоугольной системы координат в двумерном (евклидовом) пространстве. Решение одного линейного уравнения изображается как вертикальная прямая в прямоугольной системе координат для данного уравнения, но эта же прямая может быть иллюстрацией решения и другого уравнения. Каждая линия может рассматриваться как множество всех решений линейного уравнения с двумя переменными, поэтому подобные уравнения и называются линейными. В общем, множество решений линейного уравнения с n переменными образуют гиперплоскость (подпространство размерности n-1) в евклидовом пространстве с размерностью n.

Линейные уравнения применяются абсолютно во всех сферах математики и их приложениях в физике и инженерном деле отчасти потому, что нелинейные системы часто хорошо можно «приблизить» и упростить линейными уравнениями. Совокупность в виде двух и более линейных уравнений, для которой надо найти конкретное решение, является системой линейных алгебраических уравнений.

Уравнение с одной переменной

Математическое описание

Уравнение имеет вид: [math]\displaystyle{ ax+b=0, }[/math] его решение сводится к виду: [math]\displaystyle{ x=-\frac ba }[/math] в общем случае, когда a ≠ 0. «Неизвестной» называется в данном случае переменная x. Если a = 0, то возможны два варианта. В случае, если b тоже равняется нулю, решений бесконечно много, поскольку любое число является решением. Но если b ≠ 0, то у уравнения не может быть корней, поскольку [math]\displaystyle{ \not \exist x \in \mathbb R : 0 \cdot x = - b \ne 0 }[/math]. В последнем случае подобное уравнение является противоречивым (англ.) (рус. (т.е. нельзя подобрать переменную, чтобы было верным равенство)^[1].

Примеры решения

Дано линейное уравнение в виде результата умножения двух чисел; известен один из множителей, второй неизвестен, но известен результат.

[math]\displaystyle{ 3 \cdot x = 24 }[/math]

В данном случае для того, чтобы найти неизвестный множитель [math]\displaystyle{ x }[/math], результат умножения 24 нужно разделить на известный множитель 3. Результатом операции деления будет 8 как корень данного уравнения.

[math]\displaystyle{ x = \frac{24}{3} = 8 }[/math].

Линейное уравнение такого типа, как

[math]\displaystyle{ 0 \cdot x = 7, }[/math]

не имеет решения, так как результат умножения любого числа на 0 всегда даёт 0. Вместе с тем уравнение вида

[math]\displaystyle{ 0 \cdot x = 0 }[/math]

имеет бесконечно много решений. Следовательно, для него [math]\displaystyle{ x }[/math] может быть любым числом.

Уравнение с двумя переменными

Описание в общей и канонической формах

В случае, если в уравнении есть две переменные, линейное уравнение можно представить в общей форме: [math]\displaystyle{ ax+by+c=0 }[/math], где переменными являются величины x и y, а коэффициентами — a, b и c. В канонической формах это уравнение имеет вид [math]\displaystyle{ Ax + By = C, }[/math] при A = a, B = b и C = –c^[2].

Решением или корнями такого уравнения называют такую пару значений переменных [math]\displaystyle{ (x;y) }[/math], которая обращает его в тождество. Таких решений (корней) линейное уравнение с двумя переменными имеет бесконечное множество.

Существуют и другие формы линейного уравнения, к которым его можно привести с помощью простых алгебраических преобразований (прибавления одной и той же величины к уравнению, умножения или деления на одно и то же число, не равное нулю и т.д.)

Пример

Дано линейное уравнение:

[math]\displaystyle{ 3 \cdot x + 4 \cdot y = 12 }[/math]

Для определения множества всех решений можно преобразовать уравнение в функцию с зависимостью [math]\displaystyle{ y }[/math] от [math]\displaystyle{ t }[/math]. В таком случае получится

[math]\displaystyle{ x = t }[/math] и [math]\displaystyle{ y = (12 - 3 \cdot t)/4 }[/math] при [math]\displaystyle{ t \in \mathbb{R} }[/math]

Так выводится график данной функции, включающий все пары x и y, обращающим уравнение в верное равенство:

[math]\displaystyle{ f(x) = (12 - 3 \cdot x)/4 = -(3/4) \cdot x + 3 }[/math].

Линейная функция

В случае, если b ≠ 0, то уравнение [math]\displaystyle{ ax+by+c=0 }[/math] можно привести к такому виду, чтобы значение y зависело от x. Уравнение может быть представлено в таком случае в форме линейной функции [math]\displaystyle{ y = kx + m }[/math], где [math]\displaystyle{ k=-\frac{a}{b};\ m=-\frac{c}{b} }[/math] (или сразу [math]\displaystyle{ y=-\frac ab x-\frac cb. }[/math]). График функции в данном случае (т.е. геометрическая модель или иллюстрация для данного уравнения) представляет собой прямую типа [math]\displaystyle{ y=kx+m }[/math], где k — угловой коэффициент (он же [math]\displaystyle{ -\frac ab }[/math]), а m =[math]\displaystyle{ -\frac cb }[/math] — координата точки пересечения графика с осью y.

В математическом анализе линейными называются те функции, график которых является именно прямой. В линейной алгебре линейной называется функция, отображающая сумму на сумме изображений слагаемых. Таким образом, в линейной алгебре функция является линейной, если c = 0, а её график проходит через начало координат. Во избежание путаницы функции, графики которых являются произвольными линиями, называются аффинными.

Геометрический смысл

Геометрическое место точек линейного уравнения от двух переменных вида y = ax + b

Вертикальная линия уравнения x = a

Горизонтальная линия уравнения y = b

Графики линейных уравнений

Любая пара (x, y), являющаяся решением уравнения [math]\displaystyle{ ax+by+c=0 }[/math], может быть отражена в прямоугольной системе координат в виде точки в двумерном пространстве. В таком случае все решения уравнения формируют линию при условии, что a и b не равняются нулю. Верно и обратное, что каждая линия является множеством решений линейного уравнения. Само словосочетание «линейное уравнение» и имеет корни в соотношении между прямыми линиями и уравнениями: линейное уравнение с двумя переменными представляет собой уравнение, все решения которого графически представляют собой линию.

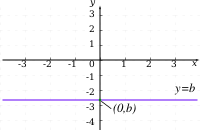
В случае, если b ≠ 0, линия является графиком функции x, описанным выше. Если b = 0, то линия будет вертикальной, параллельной оси ординат (y-оси), для уравнения [math]\displaystyle{ x=-\frac ca, }[/math], которое не является графиком функции x. Соответственно, если a ≠ 0, то линия является графиком функции y, а если a = 0 — то горизонтальной линией, параллельной оси абсцисс, для уравнения [math]\displaystyle{ y=-\frac cb. }[/math]

Уравнение с тремя и более переменными

Линейное уравнение, в котором содержится больше двух переменных, может иметь форму типа [math]\displaystyle{ a_1 x_1 + a_2 x_2 + \cdots + a_n x_n + b=0. }[/math]. Коэффициент b, иногда обозначаемый как a₀, является свободным членом. Коэффициентами могут в таком случае называть все переменные типа a_i при условии i > 0. В уравнениях с тремя неизвестными последние обозначаются буквами [math]\displaystyle{ x,\; y }[/math] и [math]\displaystyle{ z }[/math].

Решение такого уравнения — такой n-кортеж, замена каждого элемента в котором соответствующей переменной преобразовала бы уравнение в верное равенство. Чтобы уравнение имело смысл, хотя бы один коэффициент при переменной должен быть ненулевым. Если же все коэффициенты при переменных равняются нулю, то либо уравнение будет противоречивым (при b ≠ 0) как не имеющее решений, либо же любой n-кортеж будет решением данного уравнения. Все n-кортежи, которые являются решением линейного уравнения с n переменными — это координаты точек в системе координат для (n − 1)-размерной гиперплоскости в n-размерном евклидовом пространстве (или аффинном пространстве, если коэффициенты — комплексные числа или принадлежат любому полю). В случае трёх переменных эта гиперплоскость становится плоскостью (согласно одной из аксиом Евклидовой геометрии).

Если в линейном уравнении a_j ≠ 0, тогда существует решение данного уравнения для x_j [math]\displaystyle{ x_j = -\frac b{a_j} -\sum_{i\in \{1,\ldots,n\}, i\ne j} \frac {a_i}{a_j}x_i . }[/math] Если коэффициенты — вещественные числа, то таким образом определяется вещественнозначная функция для n вещественных переменных (англ.) (рус..

Пример

Дано линейное уравнение с тремя неизвестными:

[math]\displaystyle{ 3 \cdot x_1 + 2 \cdot x_2 + x_3 = 7 }[/math]

Решением данного уравнения будет являться плоскость, которой принадлежат три точки типа:

[math]\displaystyle{ x_1 = t_1, \; x_2 = t_2, \; x_3 = 7 - 3 \cdot t_1 - 2 \cdot t_2 }[/math] при [math]\displaystyle{ t_1, t_2 \in \mathbb{R} }[/math].

См. также

Примечания

↑ Уравнение противоречивое Архивная копия от 19 января 2018 на Wayback Machine (рус.)
↑ Barnett, Ziegler, Byleen, 2008, p. 15.

Литература

R.A. Barnett, M.R. Ziegler, K.E. Byleen. College Mathematics for Business, Economics, Life Sciences and the Social Sciences. — 11th. — Upper Saddle River, N.J.: Pearson, 2008. — ISBN 0-13-157225-3.
Ron Larson, Robert Hostetler. Precalculus:A Concise Course. — Houghton Mifflin, 2007. — ISBN 978-0-618-62719-6.
W.A. Wilson, J.I. Tracey. Analytic Geometry. — revised. — D.C. Heath, 1925.
Manfred Leppig. Lernstufen Mathematik. — Girardet, 1981. — С. 61–74. — ISBN 3-7736-2005-5.
Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — изд. 13-е. — М.: Наука, 1986. — 544 с.
Helmuth Preckur. Lineare Algebra und Analytische Geometrie. — München: Mentor Verlag (Mentor-Lernhilfe Band 50), 1983. — С. 72–85, 106–114. — ISBN 3-580-64500-5.

Ссылки

Hazewinkel, Michiel, ed. (2001), Linear equation, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

[1] Уравнение противоречивое Архивная копия от 19 января 2018 на Wayback Machine (рус.)

[_51c52474da482684-2] Barnett, Ziegler, Byleen, 2008, p. 15.

[1]

[2]