Формула половины стороны

Сферический треугольник

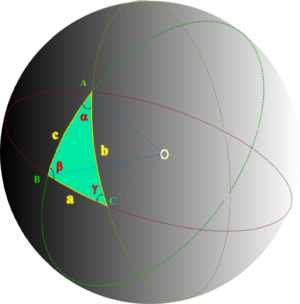
В сферической тригонометрии, формула половины стороны применяется для решения сферических треугольников.

Формула половины стороны

[math]\displaystyle{ \begin{align} \tan\left(\frac{a}{2}\right) & = R \cos (S- \alpha) \\[8pt] \tan \left(\frac{b}{2}\right) & = R \cos (S- \beta) \\[8pt] \tan \left(\frac{c}{2}\right) & = R \cos (S - \gamma) \end{align} }[/math]

где

• α, β, γ — это углы сферического треугольника,
• a, b, c — длины сторон, лежащих напротив, соответственно, углов α, β, γ,

• [math]\displaystyle{ S = \frac{1}{2}(\alpha +\beta + \gamma) }[/math]

полусумма углов треугольника, и

• [math]\displaystyle{ R=\sqrt{\frac {-\cos S}{\cos (S-\alpha) \cos (S-\beta) \cos (S-\gamma)}}. }[/math]

Интересно, что R является тангенсом радиуса описанной окружности данного сферического треугольника. Три формулы на самом деле представляют собой одну и ту же формулу, в которой лишь заменены обозначения соответствующих углов и сторон.

Вывод формулы

По теореме косинусов имеем:

[math]\displaystyle{ \cos a = \frac{\cos \alpha + \cos \beta\cos \gamma}{\sin \beta\sin \gamma}. }[/math]

Тогда по формуле двойного угла (положительный корень взят потому, что сторона меньше 180 градусов):

[math]\displaystyle{ \sin \frac{a}{2} = \sqrt{\frac{1-\cos a}{2}} = \sqrt{\frac{\sin \beta\sin \gamma - \cos \beta\cos \gamma - \cos \alpha}{2\sin \beta\sin \gamma}}. }[/math]

Применяя формулу сложения аргументов и формулу преобразования суммы функций, получаем:

[math]\displaystyle{ \sin \frac{a}{2} = \sqrt{\frac{-\cos(\beta+\gamma) - \cos \alpha}{2\sin \beta\sin \gamma}} = \sqrt{\frac{-\cos S\cos(S-\alpha)}{\sin \beta\sin \gamma}}. }[/math]

Аналогично для косинуса половины стороны получаем:

[math]\displaystyle{ \cos \frac{a}{2} = \sqrt{\frac{1+\cos a}{2}} = \sqrt{\frac{\cos(S-\beta)\cos(S-\gamma)}{\sin \beta\sin \gamma}}. }[/math]

Поэтому

[math]\displaystyle{ \operatorname{tg} \frac{a}{2} = \frac{\sin\frac{a}{2}}{\cos\frac{a}{2}} = \sqrt{\frac{-\cos S\cos(S-\alpha)}{\cos(S - \beta)\cos(S - \gamma)}} = \cos(S-\alpha)\sqrt{\frac{-\cos S}{\cos(S - \alpha)\cos(S - \beta)\cos(S - \gamma)}}. }[/math]

Двойственную к этой формуле, то есть формулу для половины угла, можно получить из неё как обычно — заменой стороны на дополнение соответствующего угла до 180 градусов и углов на дополнения соответствующих сторон до 180 градусов.

Двойственная формула

Двойственными к формулам половины стороны являются формулы для половины угла:

[math]\displaystyle{ \begin{align} \operatorname{tg}\left(\frac{\alpha}{2}\right) & = \frac{1}{\sin(s-a)}\cdot r \\[8pt] \operatorname{tg} \left(\frac{\beta}{2}\right) & = \frac{1}{\sin(s-b)}\cdot r \\[8pt] \operatorname{tg} \left(\frac{\gamma}{2}\right) & = \frac{1}{\sin(s-c)}\cdot r \end{align} }[/math]

где

• [math]\displaystyle{ s = \frac{1}{2}(a + b + c) }[/math]

полусумма сторон треугольника, и

• [math]\displaystyle{ r=\sqrt{\frac {\sin(s-a)\sin(s-b)\sin(s-c)}{\sin s}}. }[/math]

Причём в этом случае r будет тангенсом вписанной окружности сферического треугольника.

Аналогичная формула в планиметрии известна под названием теоремы котангенсов.

Применение

Формула половины стороны применяется для решения косоугольного сферического треугольника по трём сторонам, то есть когда надо по данным сторонам вычислить каждый из его углов. Формула половины угла, в свою очередь, используется для решения косоугольного треугольника по трём углам, то есть когда надо при данных трёх углах вычислить каждую из его сторон. Если же у сферического треугольника один из углов прямой, вместо этих формул для его решения применяется более удобное мнемоническое правило Непера.

См. также

• Теоремы косинусов (сферическая геометрия)
• Тригонометрические тождества