Перейти к содержанию

Мнемоническое правило Непера

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
Иллюстрация мнемонического правила Непера.

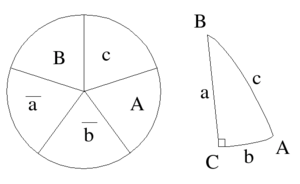
Мнемоническое правило Непера — форма записи основных соотношений в прямоугольном сферическом треугольнике, лёгкая для запоминания.

Формулировка и обоснование правила

Формулировка

Мнемоническое правило Непера можно сформулировать так[1]:

Для трёх смежных элементов прямоугольного сферического треугольника косинус среднего элемента равен произведению котангенсов соседних, а для трёх несмежных элементов косинус элемента, расположенного отдельно от других двух, равен произведению их синусов. При этом вместо катетов берутся их дополнения до 90 градусов, а прямой угол вообще не считается элементом.

Два примера:

[math]\displaystyle{ \cos B = \mathrm{ctg}\, \overline{a} \,\mathrm{ctg}\, c = \mathrm{ctg}\, (90^\circ - a) \mathrm{ctg}\, c = \frac {\mathrm{tg}\, a}{\mathrm{tg}\, c} }[/math]
[math]\displaystyle{ \cos B = \sin \overline{b} \sin A = \sin (90^\circ - b) \sin A = \cos b \sin A }[/math]

Чтобы правило было удобнее применять, рисуют круг, делят его радиусами на пять частей и записывают в них все элементы прямоугольного сферического треугольника за исключением прямого угла в той последовательности, в которой они расположены в треугольнике. Каждый катет помечают горизонтальной чертой над ним или апострофом рядом с ним — знак дополнения катета до 90 градусов. На круге нетрудно найти нужные три элемента и применить к ним мнемоническое правило.

Обоснование

Докажем одну формулу для трёх смежных элементов прямоугольного сферического треугольника и одну формулу для двух смежных и одного отдельного элемента[2], а затем для обоснования мнемонического правила Непера (а одновременно — и доказательства самих формул), дающего все десять таких формул для прямоугольного сферического треугольника, применим к этим двум формулам, следуя Ламберту, звёздчатый пятиугольник[3].

Рисунок к выводу формулы, связывающей три смежных элемента c, a, B прямоугольного сферического треугольника.

Возьмём два катета a и b (смежные элементы) и гипотенузу c (отдельный элемент). Их связывает сферическая теорема Пифагора, которая доказывается в статье о ней. Поэтому здесь доказывать в этом случае практически ничего не надо. Заметим лишь, что

[math]\displaystyle{ \cos c = \cos a \cos b = \sin (90^\circ - a) \sin (90^\circ - b) = \sin \overline{a} \sin \overline{b}, }[/math]

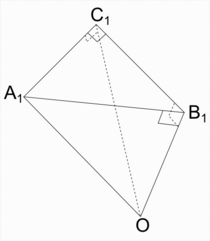
то есть для этих трёх элементов мнемоническое правило Непера справедливо. Выведем теперь формулу для трёх смежных элементов. Возьмём гипотенузу c, катет a и угол B. Как и в доказательстве сферической теоремы Пифагора, рассмотрим трёхгранный угол OA1B1C1 со сторонами (лучами) OA1, OB1, OC1 и вершиной в точке O, соответствующий данному прямоугольному сферическому треугольнику ABC.

Звёздчатый пятиугольник, с помощью которого обосновывается мнемоническое правило Непера.

Заметим, что

[math]\displaystyle{ \frac {A_1B_1}{B_1O} = \mathrm{tg}\, \angle A_1OB_1 = \mathrm{tg}\, c, }[/math]
[math]\displaystyle{ \frac {C_1B_1}{B_1O} = \mathrm{tg}\, \angle B_1OC_1 = \mathrm{tg}\, a, }[/math]
[math]\displaystyle{ \frac {C_1B_1}{A_1B_1} = \cos \angle A_1B_1C_1 = \cos B. }[/math]

Отсюда

[math]\displaystyle{ \mathrm{tg}\, a = \frac {C_1B_1}{B_1O} = \frac {A_1B_1}{B_1O} \cdot \frac {C_1B_1}{A_1B_1} = \mathrm{tg}\, c \cos B, }[/math]
[math]\displaystyle{ \cos B = \frac {\mathrm{tg}\, a}{\mathrm{tg}\, c} = \mathrm{ctg}\, (90^\circ-a) \mathrm{ctg}\, c = \mathrm{ctg}\, \overline{a} \,\mathrm{ctg}\, c, }[/math]

то есть и для этих трёх элементов мнемоническое правило Непера справедливо. Обе формулы доказаны. Остаётся применить звёздчатый пятиугольник.

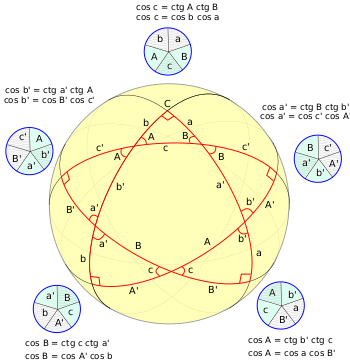
На рисунке дополнения элементов до 90 градусов обозначены апострофами. Строится этот звездчатый пятиугольник следующим образом. На сфере чертится данный сферический треугольник ABC, его вершины A и B — первые две вершины пятиугольника. Далее проводим поляры точек A и B, точка их пересечения, лежащая по другую сторону гипотенузы c от вершины C будет третьей вершиной пятиугольника, а две точки пересечения этих поляр с продолжениями сторон a и b будут остальными двумя вершинами пятиугольника. Продолжения сторон пятиугольника, пересекаясь образуют пять сферических треугольников. Нетрудно видеть, что каждая вершина пятиугольника является полюсом для его противоположной стороны. Поэтому все пять сферических треугольников будут прямоугольными. Отсюда же получаются и величины всех их элементов, обозначенные на рисунке.

Для сферического треугольника ABC выше доказаны две формулы мнемонического правила Непера. Элементы каждого следующего по часовой стрелке прямоугольного сферического треугольника соответствуют элементам предыдущего, повернутым на 2/5 полного оборота, или их дополнениям до 90 градусов. Поэтому, последовательно применяя к соответствующим элементам каждого треугольника полученные две формулы, получаем все 10 формул и такую же форму мнемонического правила Непера для всех из них.

История

Мнемоническое правило Непера названо по имени Джона Непера, который опубликовал его в своём известном сочинении «Описание удивительной таблицы логарифмов» (1614), причём он его привёл в качестве демонстрации применения определённого им в этом труде нового математического понятия логарифм, и обе части равенства в мнемоническом правиле у Непера прологарифмированы. Изящное и наглядное математическое обоснование мнемонического правила Непера с помощью звёздчатого пятиугольника было дано Иоганном Ламбертом в его труде «Дополнения к применению математики и их приложения», увидевшем свет в 1765 году[3]. Позднее звёздчатый пятиугольник на сфере был использован Карлом Гауссом для обоснования этих же (вероятно, он не читал об этом в труде Ламберта) и других свойств, Гаусс назвал его «замечательной пентаграммой» (лат. pentagramma mirificum)[4].

Обоснование при помощи звёздчатого пятиугольника соотношений в прямоугольном сферическом треугольнике оказалось в некоторой степени универсальным методом: Николай Лобачевский использовал последовательность из пяти прямоугольных треугольников для вывода зависимости между элементами прямоугольного треугольника в исследованном им пространстве, впоследствии индийский математик С. Мукопадиайа связал эту последовательность с пятиугольником в том же пространстве, а ещё позднее русский математик Александр Норден установил связь звездчатого пятиугольника на сфере с упомянутым пятиугольником в пространстве Лобачевского[3].

Примечания

  1. ↑ Степанов Н.Н. Мнемоническое правило Непера // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 48—49. — 154 с.
  2. ↑ Степанов Н.Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.
  3. ↑ 3,0 3,1 3,2 Б.Л.Лаптев. Ламберт — геометр. // Историко-математические исследования. — М.: Наука, 1980. — № 25. — С. 248-252.
  4. ↑ Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — С. xi. — 228 с.
Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Мнемоническое_правило_Непера&oldid=12728303