Тривиальные объекты в алгебре

В алгебре (разделе математики), многие алгебраические структуры имеют тривиальные, то есть простейшие объекты. Как множества, они состоят из одного элемента, обозначаемого символом «0», а сам объект — как «{0}», или просто «0» смотря по контексту (например, в точных последовательностях). Объекты, соответствующие тривиальным случаям, важны для унификации рассуждений: например, удобнее сказать, что «решения уравнения T x = 0 всегда составляют линейное пространство», нежели делать оговорку «… либо множество {0}».

Важнейшими из таких объектов являются:

Тривиальная группа, простейшая из групп.
Является также простейшей из абелевых групп, и все нижеперечисленные объекты наследуют её структуру, понимаемую как сложение.
Тривиальное кольцо, простейшее из колец.
Нулевой (тривиальный, или пустопорождённый) модуль, простейший из модулей над заданным кольцом R).
Нулевое (или нульмерное) линейное пространство над полем R, простейшее из линейных пространств.
Нулевая алгебра, простейшая из алгебр над кольцом или над полем R.

В трёх последних случаях умножение на скаляр определяется как κ0 = 0 , где κ ∈ R.

Всякая нулевая алгебра также тривиальна как кольцо. Нулевая алгебра над полем является нулевым линейным пространством, а над кольцом — нулевым модулем.

Трактовка при помощи теории категорий

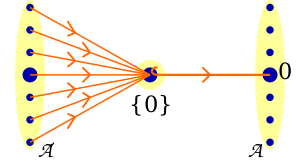
С точки зрения теории категорий, тривиальный объект является терминальным, а иногда (в зависимости от определения морфизма) нулевым (то есть одновременно терминальным и начальным) объектом.

Тривиальный объект единственнен с точностью до изоморфизма.

Терминальность тривиального объекта означает, что морфизм A → {0} существует и единственнен для любого объекта A в категории. Этот морфизм отображает всякий элемент объекта A в 0.

2↕	[math]\displaystyle{ \begin{bmatrix}0 \\ 0\end{bmatrix} }[/math]	=	[math]\displaystyle{ \begin{bmatrix} \, \\ \,\end{bmatrix} }[/math]	[ ]	‹0
	↔ 1		^ 0	↔ 1
Элемент нулевого пространства, записанный как пустой вектор-столбец (справа), умножен на пустую матрицу 2×0 для получения 2-мерного нулевого вектора (слева). Правила умножения матриц соблюдены.

В категориях Rng (колец без обязательной единицы), R-Mod и Vect_R, тривиальное кольцо, нулевые модуль и пространство соответственно являются нулевыми объектами. Нулевой объект по определению начален, то есть морфизм {0} → A существует и единственнен для любого объекта A в категории. Этот морфизм отображает 0, единственный элемент объекта {0}, в нуль 0 ∈ A. Это мономорфизм, и его образ (подмодуль/подпространство в A, порождённый нулём элементов) изоморфен {0}.

Структуры с единицей

В структурах с единицей (нейтральным элементом умножения) дело не так просто. Когда определение морфизма в категории требует их сохранения, тривиальный объект либо является только терминальным (но не начальным), либо не существует вовсе (например, когда определение структуры требует неравенство 1 ≠ 0).

В категории Ring колец с единицами, кольцо целых чисел Z является начальным объектом, а не {0}.

См. также

Ссылки

David Sharpe. Rings and factorization (неопр.). — Cambridge University Press, 1987. — С. 10 : trivial ring. — ISBN 0-521-33718-6.
Barile, Margherita. Trivial Module (англ.) на сайте Wolfram MathWorld.
Barile, Margherita. Zero Module (англ.) на сайте Wolfram MathWorld.