Теорема о циркуляции магнитного поля

Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой, и обобщил её (см. ниже). Уравнение, представляющее собой содержание теоремы в этом обобщённом виде, входит в число уравнений Максвелла. (Для случая постоянных электрических полей — то есть в принципе в магнитостатике — верна теорема в первоначальном виде, сформулированном Ампером и приведённом в статье первым; для общего случая правая часть должна быть дополнена членом с производной напряжённости электрического поля по времени — см. ниже). Теорема гласит:

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

Эта теорема, особенно в иностранной или переводной литературе, называется также теоремой Ампера или законом Ампера о циркуляции (англ. Ampère’s circuital law). Последнее название подразумевает рассмотрение закона Ампера в качестве более фундаментального утверждения, чем закон Био — Савара — Лапласа, который в свою очередь рассматривается уже в качестве следствия (что, в целом, соответствует современному варианту построения электродинамики).

Для общего случая (классической) электродинамики формула должна быть дополнена в правой части членом, содержащим производную по времени от электрического поля (см. уравнения Максвелла, а также параграф «Обобщение» ниже). В таком дополненном виде она представляет собой четвёртое уравнение Максвелла в интегральной форме.

Математическая формулировка

В математической формулировке для магнитостатики теорема имеет следующий вид:

[math]\displaystyle{ \oint\vec B \cdot \vec{dl} = \frac{4\pi}{c}\int\vec j\cdot \vec{ds} }[/math]

Здесь [math]\displaystyle{ \vec B }[/math] — вектор магнитной индукции, [math]\displaystyle{ \vec j }[/math] — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме:

[math]\displaystyle{ \mathrm{rot}\ \vec B = \frac{4\pi}{c}\vec j }[/math]

Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса.

Приведённая выше форма справедлива для вакуума. В случае применения её в среде (веществе), она будет корректна только в случае, если под j понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие в веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы (см. диамагнетики) и магнитные моменты микрочастиц (см.например ферромагнетики).

Поэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения (см. связанные токи), выразив его через величину намагниченности [math]\displaystyle{ I }[/math] и введя вектор напряжённости магнитного поля

[math]\displaystyle{ \vec H = \vec B - 4\pi \vec I }[/math]

Тогда теорема о циркуляции запишется в форме

[math]\displaystyle{ \oint\vec H\cdot \vec{dl} = \frac{4\pi}{c}\int\vec j_f\cdot \vec{ds} }[/math]

[math]\displaystyle{ \mathrm{rot}\ \vec H = \frac{4\pi}{c}\vec j_f, }[/math]

где под [math]\displaystyle{ \vec j_f }[/math] (в отличие от [math]\displaystyle{ \vec j }[/math] в формуле выше) имеются в виду т. н. свободные токи, в которых ток намагничения исключён (что бывает удобно практически, поскольку [math]\displaystyle{ \vec j_f }[/math] — это обычно уже в сущности макроскопические токи, которые не связаны с намагничением вещества и которые в принципе нетрудно непосредственно измерить).

В динамическом случае — то есть в общем случае классической электродинамики — когда поля меняются во времени (а в средах при этом меняется и их поляризация) — и речь тогда идёт об обобщённой теореме, включающей [math]\displaystyle{ d\vec E/dt }[/math], — всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене [math]\displaystyle{ d\vec D/dt }[/math].

Обобщение

Основная статья: Закон Ампера — Максвелла

Основным фундаментальным обобщением теоремы является четвёртое уравнение Максвелла. В интегральной форме оно является прямым обобщением на динамический случай магнитостатической формулы, приведённой выше. Для вакуума:

[math]\displaystyle{ \oint\vec B \cdot \vec{dl} = \frac{1}{c} \int(4\pi \vec j + \frac{\partial \vec E}{\partial t})\cdot \vec{ds} }[/math]

для среды:

[math]\displaystyle{ \oint\vec{H}\cdot \vec{dl} = \frac{4\pi}{c} \int \vec j \cdot \vec{ds} + \frac{1}{c}\frac{\partial}{\partial t}\int\vec{D}\cdot \vec{ds}. }[/math]

(Как видим, формулы отличаются от приведённых выше только одним добавочным членом со скоростью изменения электрического поля в правой части).

Дифференциальная форма этого уравнения:

[math]\displaystyle{ \mathbf{rot}\vec{B} = \frac{4\pi}{c}\vec j + \frac{1}{c}\frac{\partial}{\partial t}\vec{E}, }[/math]

[math]\displaystyle{ \mathbf{rot}\vec{H} = \frac{4\pi}{c}\vec j + \frac{1}{c}\frac{\partial}{\partial t}\vec{D} }[/math]

(в гауссовой системе, для вакуума и среды соответственно) — также можно при желании считать вариантом обобщения теоремы о циркуляции магнитного поля, поскольку она, конечно, тесно связана с интегральной.

Практическое значение

Магнитное поле прямолинейного проводника с током.

Теорема о циркуляции играет в магнитостатике приблизительно ту же роль, что и теорема Гаусса в электростатике. В частности, при наличии определённой симметрии задачи, она позволяет просто находить величину магнитного поля во всём пространстве по заданным токам. Например, для вычисления магнитного поля от бесконечного прямолинейного проводника с током по закону Био — Савара — Лапласа потребуется вычислить неочевидный интеграл, в то время как теорема о циркуляции (с учётом осевой симметрии задачи) позволяет дать мгновенный ответ:

[math]\displaystyle{ B(r)\cdot 2\pi r = \frac{4\pi}{c} I \to B(r) = \frac{2I}{cr} }[/math].

Доказательство теоремы о циркуляции

Циркуляция магнитного поля

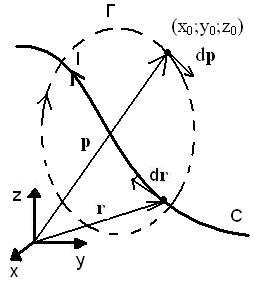
Если теорема о циркуляции магнитного поля не принимается в качестве аксиомы, то она может быть доказана с помощью закона Био — Савара — Лапласа. Рассмотрим магнитное поле, создаваемое в точке [math]\displaystyle{ \vec p = (x_0;y_0;z_0) }[/math] бесконечным проводом с током, заданным в пространстве кривой C. По закону Био — Савара — Лапласа токовый элемент провода, заданный радиус-вектором [math]\displaystyle{ \vec r }[/math], создаёт в точке [math]\displaystyle{ \vec p }[/math] элементарное поле [math]\displaystyle{ \mathrm{d}\vec B (\vec p) = {\mu_0 \over 4\pi} \frac{I[\mathrm{d}\vec{r} \times (\vec{p} - \vec{r})]}{|\vec p - \vec r|^3} }[/math].

Полная индукция магнитного поля в точке [math]\displaystyle{ \vec p }[/math] получается интегрированием элементарного поля по всей кривой C в направлении течения тока:

[math]\displaystyle{ \vec B (\vec{p}) = {\mu_0 \over 4\pi} \int\limits_\Complex \frac{I[\mathrm{d}\vec{r} \times (\vec{p} - \vec{r})]}{|\vec p - \vec r|^3} }[/math]

Нужно сразу отметить, что полученный интеграл не относится ни к одному из двух родов криволинейных интегралов. Как можно заметить, он определяет собой векторную величину, тогда как любой криволинейный интеграл является скалярной величиной. Но допустим, что его всё-таки можно вычислить каким-нибудь способом (например, интегрированием отдельно каждой компоненты вектора). Тогда найдём циркуляцию полученного вектора индукции по некоторому замкнутому контуру Г, обхватывающему провод с током.

По определению циркуляция векторной функции — это криволинейный интеграл второго рода от этой функции по замкнутому контуру в положительном направлении обхода этой кривой. Будем считать положительным направлением нормали к поверхности, натянутой на контур, такое направление, которое образует острый угол с осью z. Тогда положительное направление обхода контура определяется правилом буравчика (правого винта) по отношению к положительной нормали. Будем также считать положительным тот ток, который течёт в направлении положительной нормали контура, охватывающего ток.

Циркуляция будет иметь вид:

[math]\displaystyle{ \Gamma=\oint_{\Gamma} \vec{B} \cdot \mathrm{d}\vec p = \oint_{\Gamma}{\mu_0I \over 4\pi} \int\limits_\Complex \frac{[\mathrm{d}\vec{r} \times (\vec{p} - \vec{r})]}{|\vec p - \vec r|^3}\cdot \mathrm{d}\vec p }[/math]

Можно заметить, что под знаками интегралов появилось смешанное произведение векторов [math]\displaystyle{ [\mathrm{d}\vec{r} \times (\vec{p} - \vec{r})]\cdot \mathrm{d}\vec p=(\mathrm{d}\vec p,\mathrm{d}\vec{r},(\vec{p} - \vec{r})) }[/math], которое по свойству кососимметрии может быть записано следующим образом:

[math]\displaystyle{ [\mathrm{d}\vec{r} \times (\vec{p} - \vec{r})]\cdot \mathrm{d}\vec p=(\mathrm{d}\vec p,\mathrm{d}\vec{r},(\vec{p} - \vec{r}))=((\vec{p} - \vec{r}),\mathrm{d}\vec p,\mathrm{d}\vec r)=[\mathrm{d}\vec{p} \times \mathrm{d}\vec{r}]\cdot (\vec{p} - \vec{r}) }[/math]

Тогда циркуляция примет вид:

[math]\displaystyle{ \Gamma= {\mu_0I \over 4\pi}\oint_{\Gamma} \int\limits_\Complex(\vec{p} - \vec{r})\cdot \frac{[\mathrm{d}\vec{p} \times \mathrm{d}\vec{r}]}{|\vec p - \vec r|^3} }[/math]

Нужно обратить внимание на то, чем является векторное произведение [math]\displaystyle{ [\mathrm{d}\vec{p} \times \mathrm{d}\vec{r}] }[/math]: его величина равна площади параллелограмма, построенного на этих векторах, а направление перпендикулярно этому параллелограмму. Тогда данное векторное произведение можно считать элементарной векторной площадкой [math]\displaystyle{ \mathrm{d}\vec{S}=[\mathrm{d}\vec{p} \times \mathrm{d}\vec{r}] }[/math] поверхности, которую заметает вектор [math]\displaystyle{ (\vec{p} - \vec{r}) }[/math] при двойном криволинейном интегрировании, причём угол между [math]\displaystyle{ (\vec{p} - \vec{r}) }[/math] и [math]\displaystyle{ \mathrm{d}\vec{S} }[/math], как можно заметить, является острым. Данная поверхность является цилиндрической поверхностью, охватывающей провод с током, а её сечением является контур циркуляции Г. Тогда двойной криволинейный интеграл можно заменить поверхностным интегралом второго рода по данной поверхности.

Тогда циркуляция примет вид:

[math]\displaystyle{ \Gamma= {\mu_0I \over 4\pi}\int\!\!\!\int_S(\vec{p} - \vec{r})\cdot \frac{\mathrm{d}\vec{S}}{|\vec p - \vec r|^3} }[/math]

Если считать поверхность интегрирования стягивающей поверхностью, легко видеть, что поверхностный интеграл представляет собой телесный угол для данной поверхности. Поверхность интегрирования условно можно считать замкнутой на бесконечности. И тогда, поскольку вектор [math]\displaystyle{ (\vec{p} - \vec{r}) }[/math] при интегрировании всегда находится внутри поверхности, телесный угол является полным, то есть равным [math]\displaystyle{ 4\pi }[/math] стерадиан. И тогда циркуляция равна [math]\displaystyle{ \Gamma= {\mu_0I \over 4\pi}4\pi=\mu_0I }[/math].

Если бы контур Г не охватывал провод, тогда вектор [math]\displaystyle{ (\vec{p} - \vec{r}) }[/math] при интегрировании никогда не находился бы полностью внутри поверхности интегрирования. В этом случае телесный угол был бы равен нулю, как и циркуляция поля: [math]\displaystyle{ \Gamma= 0 }[/math].

Последние два утверждения о телесном угле являются по сути содержанием теоремы Гаусса о потоке вектора напряжённости заряда через произвольную замкнутую поверхность и могут быть доказаны независимо.

Если бы ток тёк в противоположном направлении, угол между векторами [math]\displaystyle{ (\vec{p} - \vec{r}) }[/math] и [math]\displaystyle{ [\mathrm{d}\vec{p} \times \mathrm{d}\vec{r}] }[/math] был бы уже тупым (нормаль была бы направлена внутрь поверхности), и циркуляция поменяла бы свой знак на противоположный, что эквивалентно течению тока в прежнем направлении, но с отрицательной силой.

В случае поля, создаваемого несколькими проводниками с током, нужно помнить о свойстве суперпозиции магнитного поля и свойстве аддитивности криволинейного интеграла: циркуляция суперпозиции векторов равна скалярной сумме циркуляций этих векторов.