Модель Рамсея — Касса — Купманса

Модель Рамсея — Касса — Купманса (модель Рамсея, неоклассическая модель экономического роста, англ. Ramsey—Cass—Koopmans model) — неоклассическая модель экзогенного экономического роста в условиях совершенной конкуренции. Внесла вклад в понимание того, каким образом решения индивидов формируют норму сбережений в экономике. Оптимальная динамика потребления из модели (правило Кейнса — Рамсея) оказалась удачной заменой экзогенной норме сбережений и затем применялась и в более поздних моделях экономического роста. Вместе с тем, модель не даёт удовлетворительного объяснения межстрановым различиям в уровне дохода на душу населения. Разработана одновременно и независимо друг от друга Тьяллингом Купмансом и Дэвидом Кассом[англ.] с использованием идей Фрэнка Рамсея в 1963 году.
История создания
В первых моделях экономического роста (модель Солоу, модель Харрода — Домара) использовались экзогенно задаваемые параметры: «норма сбережений» и «темп научно-технического прогресса», от которых, в конечном итоге, и зависят темпы роста экономики. Исследователи же хотели получить обоснование темпов экономического роста внутренними (эндогенными) факторами, поскольку модели с нормой сбережений имели ряд недостатков. Эти модели не объясняли устойчивые различия в уровнях и темпах роста между развивающимися и развитыми странами. Для объяснения нормы сбережений как следствия решений экономических агентов, исследователи обратились к работе Фрэнка Рамсея «Математическая теория сбережений»[1], опубликованной в The Economic Journal[англ.] ещё в декабре 1928 года. В ней была выведена межвременная функция полезности потребителя и найдено условие оптимального выбора потребителя. Используя идеи Фрэнка Рамсея, будущий лауреат Нобелевской премии по экономике Тьяллинг Купманс в работе «Оптимальный рост в агрегированной модели накопления капитала», опубликованной как «работа для обсуждения» в Йельском университете 6 декабря 1963 года[2], и изданной в более подробной версии в сборнике The Econometric Approach to Development Planning в 1965 году[3], и Дэвид Касс[англ.] в работе «Оптимальный рост в агрегированной модели накопления капитала», изданной в июле 1965 года в журнале The Review of Economic Studies[англ.][4] представили модель Рамсея — Касса — Купманса[5][6][7][8] (также известную как модель Рамсея[5][6][9], неоклассическая модель экономического роста[5]), главной особенностью которой стало определение нормы сбережений в ходе решения задач оптимизации потребителями и фирмами, взаимодействующими в условиях совершенной конкуренции[5][6].
Работы Дэвида Касса и Тьяллинга Купманса фактически излагают одинаковую модель (за исключением условия трансверсальности, введенного Кассом). Хотя работа Касса опубликована позже и в ней есть ссылка на работу Купманса[4], при этом Купманс, в свою очередь, в изданной полной версии работы, в которой также появляется условие трансверсальности, ссылается на диссертацию Касса[3]. Оба исследователя предполагали, что пришли к этой модели «одновременно и независимо друг от друга». Подробно история с названием данной модели изложена в работе Стивена Спира и Уоррена Янга «Оптимальные сбережения и оптимальный рост: модель Рамсея — Малинво — Купманса»[10]. В ней авторы отмечают вклад Эдмона Малинво, который сформулировал условие трансверсальности раньше Касса, однако не применил его к рассматриваемой модели.
Описание модели
Базовые предпосылки модели
В модели рассматривается закрытая экономика. Фирмы максимизируют свою прибыль, а потребители — полезность. Фирмы функционируют в условиях совершенной конкуренции. Производится только один продукт [math]\displaystyle{ Y }[/math], используемый, как для потребления [math]\displaystyle{ C }[/math], так и для инвестиций [math]\displaystyle{ I }[/math]. Темпы технологического прогресса [math]\displaystyle{ g }[/math], роста населения [math]\displaystyle{ n }[/math] и норма выбытия капитала [math]\displaystyle{ \delta }[/math] — постоянны и задаются экзогенно. В качестве работника и потребителя в модели выступает бесконечно живущий индивид (или домохозяйство). Предполагается, что между разными поколениями существуют альтруистические связи, при принятии решений домохозяйство учитывает ресурсы и потребности не только настоящих, но и будущих своих членов, что делает его решения аналогичным решениям бесконечно живущего индивида. Время [math]\displaystyle{ t }[/math] изменяется непрерывно[3][4][11][12].
Доходы индивида состоят из заработной платы [math]\displaystyle{ w_t }[/math] и поступлений от активов [math]\displaystyle{ ra_t }[/math]. Активы индивида [math]\displaystyle{ a_t }[/math] могут быть как положительными, так и отрицательными (долг). Процентная ставка [math]\displaystyle{ r_t }[/math] по доходам с активов и по долгу в модели принята одинаковой. В связи с этим в модели присутствует условие отсутствия схемы Понци (финансовой пирамиды): нельзя бесконечно выплачивать старые долги за счет новых[13]:
- [math]\displaystyle{ \lim_{t \to \infty}a_te^{-\int\limits_{0}^{t}(r(\nu)-n)d\nu}\geq0 }[/math],
- где [math]\displaystyle{ a_t=\frac{K_t}{L_t}=k_t }[/math] — в закрытой экономике весь капитал принадлежит резидентам, а величина активов индивида [math]\displaystyle{ a }[/math] совпадает с запасом капитала на одного работающего [math]\displaystyle{ k }[/math].
Предпосылка о закрытой экономике означает, что произведенный продукт тратится на инвестиции и потребление, экспорт и импорт отсутствуют, сбережения равны инвестициям: [math]\displaystyle{ S=I }[/math], [math]\displaystyle{ Y=C+I }[/math][14].
Производственная функция [math]\displaystyle{ Y(K,L,E) }[/math] удовлетворяет неоклассическим предпосылкам[15][16]:
1) технологический прогресс увеличивает производительность труда (нейтрален по Харроду): [math]\displaystyle{ Y_t=Y(K_t, L_tE_t), E_t=e^{gt}, g = const }[/math].
2) в производственной функции используются труд [math]\displaystyle{ L }[/math] и капитал [math]\displaystyle{ K }[/math], она обладает постоянной отдачей от масштаба: [math]\displaystyle{ Y(a K,a LE)=a Y(K,LE) }[/math].
3) предельная производительность факторов положительная и убывающая: [math]\displaystyle{ \frac{\partial Y}{\partial K}\gt 0, \frac{\partial^2 Y}{\partial K^2}\lt 0,\frac{\partial Y}{\partial L}\gt 0, \frac{\partial^2 Y}{\partial L^2}\lt 0 }[/math].
4) производственная функция удовлетворяет условиям Инады, а именно, если запас одного из факторов бесконечно мал, то его предельная производительность бесконечно велика, если же запас одного из факторов бесконечно велик, то его предельная производительность бесконечно мала: [math]\displaystyle{ \lim_{K \to 0}{\frac{\partial Y}{\partial K}}=\lim_{L \to 0}{\frac{\partial Y}{\partial L}}=+\infin, \lim_{K \to +\infin}{\frac{\partial Y}{\partial K}}=\lim_{L \to +\infin}{\frac{\partial Y}{\partial L}}=0 }[/math].
5) для производства необходим каждый фактор: [math]\displaystyle{ Y(K,0)=Y(0,LE)=0 }[/math].
Население [math]\displaystyle{ L_t }[/math], равное в модели совокупным трудовым ресурсам, растет с постоянным темпом [math]\displaystyle{ n }[/math][17]: [math]\displaystyle{ L_t = e^{nt}, n = const }[/math][17].
Индивид предлагает одну единицу труда (предложение труда неэластично) и получает натуральную заработную плату (в единицах товара). Функция полезности бесконечно живущего индивида-потребителя имеет вид[17][2]:
- [math]\displaystyle{ U=\int^{\infty}_0 u(c_t)e^{-(\rho-n) t}dt }[/math],
- где [math]\displaystyle{ c_t=\frac{C_t}{L_t} }[/math] — потребление на душу населения в момент времени [math]\displaystyle{ t }[/math]; [math]\displaystyle{ \rho }[/math] — коэффициент межвременного предпочтения потребителя,[math]\displaystyle{ \rho \gt 0, \rho = const }[/math].
Функция полезности [math]\displaystyle{ u(c_t) }[/math] является сепарабельной, то есть потребление прошлых и будущих периодов не влияют на текущую полезность, влияет только потребление текущего периода. Она удовлетворяет условиям [math]\displaystyle{ u'(c)\gt 0, u''(c)\lt 0 }[/math] и условиям Инады (при потреблении, стремящемся к нулю, предельная полезность стремится к бесконечности, при потреблении, стремящемся к бесконечности, предельная полезность стремится к нулю)[18][4]: [math]\displaystyle{ \lim_{c \to 0} u'(c)=+\infin; \lim_{c \to \infty}u'(c)=0 }[/math].
Для поиска решения модели используются удельные показатели: выпуск на единицу труда [math]\displaystyle{ y=\frac{Y}{L} }[/math], выпуск на единицу эффективного труда [math]\displaystyle{ \hat{y}=\frac{Y}{LE} }[/math], запас капитала на единицу эффективного труда [math]\displaystyle{ \hat{k}=\frac{K}{LE} }[/math], потребление на единицу эффективного труда [math]\displaystyle{ \hat{c}=\frac{C}{LE} }[/math][19].
Задача потребителя
Доходы индивида расходуются либо на потребление, либо на увеличение активов (сбережений). Население растет темпом [math]\displaystyle{ n }[/math], поэтому активы на одного человека сокращаются с этим же темпом, то есть скорость изменения активов в каждый момент времени уменьшается на [math]\displaystyle{ na_t }[/math]. Таким образом, производная активов по времени [math]\displaystyle{ \dot{a} }[/math], выступающая в качестве бюджетного ограничения индивида, имеет вид[20]:
- [math]\displaystyle{ \dot{a}=w_t+r_ta_t-c-na_t }[/math].
Задача потребителя заключается в максимизации полезности [math]\displaystyle{ U }[/math] при бюджетном ограничении и при ограничении на отсутствие схемы Понци. Поскольку бюджетное ограничение представлено как производная по времени, то задача потребителя представлена в виде задачи динамической оптимизации. Её решение можно найти путём построения функция Гамильтона и нахождения её максимума с помощью принципа максимума Понтрягина[21][22].
Функция Гамильтона выглядит следующим образом:
- [math]\displaystyle{ H=u(c)e^{-(\rho-n) t}+\lambda_t (w_t+r_ta_t-c-na_t) }[/math]
- при условии:
- [math]\displaystyle{ \lim_{t \to \infty}a_te^{-\int\limits_{0}^{t}(r(\nu)-n)d\nu}\geq0 }[/math].
Условие максимума первого порядка: [math]\displaystyle{ \frac{\partial H}{\partial c}= u'(c)e^{-(\rho-n) t}-\lambda_t=0 }[/math].
Фазовая координата (сопряжённое уравнение): [math]\displaystyle{ \frac{\partial H}{\partial a}=(r_t-n)\lambda_t=-\dot{\lambda} }[/math], где [math]\displaystyle{ \dot{\lambda} }[/math] — производная [math]\displaystyle{ \lambda }[/math] по времени.
Условие трансверсальности (при невыполнении которого найденное решение может оказаться не максимумом, а седловой точкой): [math]\displaystyle{ \lim_{t \to \infty}\lambda_ta_t=0 }[/math], где [math]\displaystyle{ \lambda_t }[/math] представляют собой теневые цены[англ.] активов[21] (теневые цены учитывают внешние эффекты в стоимости товаров, если фирмы и потребители принимают решения в соответствии со структурой цен, пропорциональной теневой, то в экономике достигается оптимальное по Парето состояние). В данном случае условие трансверсальности совпадает с ограничением на отсутствие схемы Понци[13][23].
Искомое решение имеет вид[24][25]:
- [math]\displaystyle{ r_t-n=\rho-n-\biggl(\frac{u''(c)}{u'(c)}c\biggr)\frac{\dot{c}}{c} }[/math],
- где [math]\displaystyle{ \dot{c} }[/math] — производная потребления по времени, [math]\displaystyle{ \frac{u''(c)}{u'(c)}c }[/math] — эластичность предельной полезности по потреблению.
Поскольку для дальнейшего анализа необходимо, чтобы эта величина была постоянной, вводится дополнительная предпосылка о виде функции полезности: в качестве неё используют функцию с постоянной эластичностью замещения[26]:
- [math]\displaystyle{ u(c)=\frac {c^{1-\theta}-1} {1-\theta} }[/math].
В таком случае, [math]\displaystyle{ \frac{u''(c)}{u'(c)}c=-{\theta} }[/math], а значит[25]:
- [math]\displaystyle{ \frac {\dot{c}}{c}= \frac {1}{\theta}(r_t-\rho) }[/math],
- где [math]\displaystyle{ \dot{c} }[/math] — производная потребления на душу населения по времени.
Найденное решение называется правилом Кейнса — Рамсея. Оно было получено Фрэнком Рамсеем, а содержательную интерпретацию ему дал Джон Кейнс[1][27].
Задача фирмы
Производственную функцию [math]\displaystyle{ Y=f(K, LE)=f(\hat{k})LE }[/math] можно записать через удельные показатели: [math]\displaystyle{ \hat{y}=f(\hat{k}) }[/math]. Задача фирмы состоит в максимизации прибыли [math]\displaystyle{ \pi }[/math][28]:
- [math]\displaystyle{ \pi=f(K_t,L_tE_t)-(r+\delta)K_t-wL_t=L_tE_t\biggl(f(\hat{k_t})-(r+\delta)\hat{k_t}-\frac{w}{E_t}\biggr) \rightarrow \max }[/math]
Поскольку фирмы функционируют в условиях совершенной конкуренции, то предельные производительности факторов производства равны их ценам[15][28]:
- [math]\displaystyle{ \frac{\partial Y_t}{\partial K}= f'(\hat{k_t})=r_t+\delta }[/math],
- [math]\displaystyle{ \frac{\partial Y_t}{\partial L}=(f(\hat{k_t})-\hat{k_t} f'(\hat{k_t}))e^{gt}=w_t }[/math].
Общее экономическое равновесие

Учитывая, что [math]\displaystyle{ a=k }[/math], подставив полученные из решения задачи фирмы значения [math]\displaystyle{ r }[/math] и [math]\displaystyle{ w }[/math] в уравнение динамики активов, получим[29]:
- [math]\displaystyle{ \dot\hat{k}=f(\hat{k_t})-\hat{c}-(\delta+n+g)\hat{k_t} }[/math].
Поскольку [math]\displaystyle{ \frac{\dot {\hat {c}}}{\hat{c}}= \frac{\dot {c}}{c}-g }[/math][30], решение задачи потребителя можно записать в следующем виде[31]:
- [math]\displaystyle{ \frac{\dot {\hat {c}}}{\hat{c}}=\frac{1}{\theta}(r_t-\rho-g\theta)=\frac{1}{\theta}(f'(\hat{k_t})-\delta-\rho-\theta g\biggr) }[/math].
В стационарном состоянии [math]\displaystyle{ \dot\hat{c}=\dot\hat{k}=\dot\hat{y}=0 }[/math]. Откуда, получаем, что [math]\displaystyle{ f'(\hat{k_t})=\delta+\rho+\theta g }[/math]. В итоге, устойчивое состояние описывается системой уравнений[30][29]:
- [math]\displaystyle{ \begin{cases} \hat{c}^*=f(\hat{k}^*)-(\delta+n+g)\hat{k}^*, \\ f'(\hat{k}^*)=\delta+\rho+\theta g, \end{cases} }[/math]
- где [math]\displaystyle{ \hat{c}^* }[/math] — потребление, а [math]\displaystyle{ \hat{k}^* }[/math] — капиталовооружённость на единицу эффективного труда в устойчивом состоянии.
По условию трансверсальности[29]:
- [math]\displaystyle{ \lim_{t \to \infin}\biggl(\hat{k}_te^{-\int\limits_{0}^{t}({f'(\hat{k}_\nu)-\delta-g-n})d\nu}\biggr)=0 }[/math],
откуда следует что [math]\displaystyle{ f'(\hat{k})\gt \delta+n+ g }[/math]. С учетом уравнения для [math]\displaystyle{ \frac{\dot\hat{c}}{\hat{c}} }[/math], это условие означает, что для существование устойчивого состояния необходимо, чтобы [math]\displaystyle{ \rho+\theta g\gt g+n }[/math]. Также это означает, что в модели Рамсея — Касса — Купманса накопление капитала ниже, чем уровень максимизирующий потребление (модифицированное Золотое правило: [math]\displaystyle{ \frac{\partial f(\hat{k}^{**})}{\partial k}=\delta+n+ g }[/math], где [math]\displaystyle{ \hat{k}^{**} }[/math] — капиталовооружённость на единицу эффективного труда, соответствующая Золотому правилу), а значит, невозможна динамическая неэффективность в виде избыточного накопления капитала[32][33].
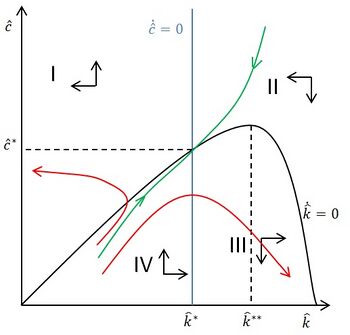
Достижение равновесия в модели можно проиллюстрировать при помощи фазовой плоскости. Линии [math]\displaystyle{ \dot\hat{c}=0 }[/math] и [math]\displaystyle{ \dot\hat{k}=0 }[/math] делят диаграмму на четыре квадранта. Слева от линии [math]\displaystyle{ \dot\hat{c}=0 }[/math] траектория капиталовооружённости идет вверх, а справа от линии [math]\displaystyle{ \dot\hat{c}=0 }[/math] — вниз. Выше линии [math]\displaystyle{ \dot\hat{k}=0 }[/math] траектория капиталовооружённости идет влево, а ниже линии [math]\displaystyle{ \dot\hat{k}=0 }[/math] — вправо. Таким образом, в квадранте I траектория идет влево и вверх, в квадранте II — влево и вниз, в квадранте III — вправо и вниз, в квадранте IV — вправо и вверх. В итоге, в модели существует только одна траектория, ведущая к равновесию — зеленая линия на иллюстрации. На этой линии расположено множество точек [math]\displaystyle{ \hat{c}_0 }[/math] и [math]\displaystyle{ \hat{k}_0 }[/math], из которых система приходит в устойчивое состояние. Варианты траектории из других точек показаны красным, в этом случае в конечном итоге становится равной нулю либо капиталовооружённость ([math]\displaystyle{ \hat{k}=0 }[/math]), либо потребление ([math]\displaystyle{ \hat{c}=0 }[/math])[34]. Поскольку оптимальная траектория капиталовооружённости в модели имеет вид седла, её также называют «седловой путь»[35].
Динамика нормы сбережений по мере приближения к равновесному состоянию также показана на иллюстрации.
В рассматриваемой модели равновесия для централизованной и децентрализованной экономики одинаковы[36].
Конвергенция
Модель предполагает наличие условной конвергенции, то есть, что страны с малым уровнем капиталовооружённости будут расти более высокими темпами, чем страны с большим уровнем капиталовооружённости [math]\displaystyle{ k }[/math], при условии, что устойчивое состояние у них одинаково. Скорость приближения к устойчивому состоянию можно оценить при помощи линейной аппроксимации посредством разложения в ряд Тейлора дифференциальных уравнений для [math]\displaystyle{ \dot\hat{c} }[/math] и [math]\displaystyle{ \dot\hat{k} }[/math][37]:
- [math]\displaystyle{ \begin{cases} \dot\hat{c}\approx\frac{\partial \dot\hat{c}}{\partial \hat{k_t}}\vert_{\hat{k_t}=\hat{k}^*}(\hat{k_t}-\hat{k}^*) +\frac{\partial \dot\hat{c}}{\partial \hat{c_t}}\vert_{\hat{c_t}=\hat{c}^*}(\hat{c_t}-\hat{c}^*), \\ \dot\hat{k}\approx\frac{\partial \dot\hat{k}}{\partial \hat{k_t}}\vert_{\hat{k}=\hat{k}^*}(\hat{k_t}-\hat{k}^*) +\frac{\partial \dot\hat{k}}{\partial \hat{c}_t}\vert_{\hat{c_t}=\hat{c}^*}(\hat{c_t}-\hat{c}^*). \end{cases} }[/math]
Из условий устойчивости следует, что угловой коэффициент у второго слагаемого ([math]\displaystyle{ c_t-\hat{c}^* }[/math]) во втором уравнении равен -1, а в первом — 0. Используя уравнения устойчивого состояния, можно записать линейные аппроксимации в следующем виде[38]:
- [math]\displaystyle{ \begin{cases} \dot\hat{c}\approx \frac{f''(\hat{k}^*)\hat{c}}{\theta}(\hat{k_t}-\hat{k}^*),\\ \dot\hat{k}\approx(\rho+\theta g - g)(\hat{k_t}-\hat{k}^*)-(\hat{c_t}-\hat{c}^*). \end{cases} }[/math]
Решение этой системы уравнений имеет вид[38]:
- [math]\displaystyle{ \begin{cases} \hat{k}_t-\hat{k}^*=(\hat{k}_0-\hat{k}^*)e^{\mu t}, \\ \hat{c}_t-\hat{c}^*=(\hat{c}_0-\hat{c}^*)e^{\mu t}, \end{cases} }[/math]
- где [math]\displaystyle{ \mu }[/math] — коэффициент, характеризующий скорость конвергенции.
Расчеты скорости конвергенции по модели Рамсея — Касса — Купманса с использованием параметров, близких к параметрам экономики США, предсказывают высокую скорость конвергенции, не наблюдаемую на реальных данных[39].
Фискальная политика в модели

Модель позволяет оценить влияние фискальной политики на равновесие. Предполагается, что величина налогов предполагается равной величине государственных расходов, которые не влияют на полезность индивидов и будущий выпуск. В этом случае уравнение для [math]\displaystyle{ \dot\hat{k} }[/math] примет следующий вид[40]:
- [math]\displaystyle{ \dot\hat{k}=f(\hat{k_t})-\hat{c}-\hat{G}-(\delta+n+g)\hat{k_t} }[/math],
- где [math]\displaystyle{ \hat{G} }[/math] — величина государственных расходов на единицу труда с постоянной эффективностью.
В результате фискальной политики кривая [math]\displaystyle{ \dot\hat{k}=0 }[/math] сдвигается вниз на величину [math]\displaystyle{ \hat{G} }[/math] и равновесие в модели устанавливается на прежнем уровне капиталовооружённости, но потребление снизится на величину [math]\displaystyle{ \hat{G} }[/math]. Таким образом, в модели государственные расходы вытесняют потребление[41].
Влияние фискальной политики на равновесие проиллюстрировано при помощи фазовой плоскости.
Преимущества, недостатки и дальнейшее развитие модели
Наиболее важный вклад модели Рамсея — Касса — Купманса состоит в том, что она раскрыла механизм формирования нормы сбережений через решения потребителей, а также стала основой для дальнейшего анализа того, как решения индивидов формируют накопления физического и человеческого капитала, и как следствие, научно-технический прогресс. Это стало большим шагом вперёд по сравнению с моделью Солоу, и во многом по этой причине модель стала отправной точкой для многих исследователей, которые использовали её концептуальный и математический аппарат для построения своих моделей[42]. Неоклассическая модель экономического роста рассматривается во всех современных учебниках макроэкономики и теории экономического роста[43].
Оптимальная динамика потребления из модели (правило Кейнса — Рамсея) оказалась удачной заменой экзогенной норме сбережений и затем применялась и в более поздних моделях экономического роста, где в качестве экономического агента выступает бесконечно живущий индивид (или домохозяйство): в АК-модели, модели обучения в процессе деятельности, модели Удзавы — Лукаса, модели растущего разнообразия товаров[42].
Включение в модель внешних эффектов от уровня физического и человеческого капитала (для чего в некоторых случаях пришлось отказаться от 2, 3 и 4 предпосылки неоклассической производственной функции) привело к развитию АК-моделей[44].
Мигель Сидрауски добавил в модель денежную массу, чтобы проанализировать влияние денежной эмиссии и инфляции на реальные показатели в экономике. В итоге в расширенной модели равновесие получилось таким же, как и в модели без денежной массы, что означает отсутствие влияния предложения денег на реальные показатели. Полученное свойство было названо нейтральностью денег[45].
В качестве недостатка модели некоторые исследователи указывали бесконечно живущего индивида (или домохозяйство) в качестве вечного потребителя[46]. По мере взросления характер потребительского поведения меняется. Если в молодом возрасте индивид работает и делает сбережения, то в старости он эти сбережения тратит[47]. Этот факт был отражен в модели пересекающихся поколений, которая полностью отрицает альтруистические связи между поколениями[48][46].
Вместе с тем, модель не внесла существенного вклада в понимание причин межстрановых различий в уровне ВВП на душу населения и темпах его роста. Модель предполагает наличие условной конвергенции, что означает, что бедные страны должны расти быстрее богатых при условии схожести структурных параметров, но в реальности этого не происходит, как показали, например, исследования Р. Холла и Ч. Джонса[49], Дж. Де Лонга[50], П. Ромера[51]. Есть лишь единичные примеры (японское экономическое чудо, корейское экономическое чудо) когда бедные страны смогли догнать богатые по уровню ВВП на душу населения, в большинстве своём сближения уровня развития не происходит[52]. Также, как и в модели Солоу, научно-технический прогресс в модели Рамсея — Касса — Купманса не является следствием принятия решений экономическими агентами, а задается экзогенно[43].
В модели невозможна динамическая неэффективность, решения для централизованной и децентрализованной экономики одинаковы, а значит невозможно неоптимальное по Парето равновесие в экономике, потому модель не показывает, как неправильная экономическая политика или ограничивающие социальные институты могут замедлить развитие страны. Другими словами, модель не объясняет причин, по которым бедные страны остаются бедными и не могут догнать богатые[43].
Примечания
- ↑ 1,0 1,1 Ramsey F., 1928.
- ↑ 2,0 2,1 Koopmans, 1963.
- ↑ 3,0 3,1 3,2 Koopmans T., 1965.
- ↑ 4,0 4,1 4,2 4,3 Cass, 1965.
- ↑ 5,0 5,1 5,2 5,3 Аджемоглу, 2018, с. 437.
- ↑ 6,0 6,1 6,2 Туманова, Шагас, 2004, с. 228.
- ↑ Барро, Сала-и-Мартин, 2010, с. 115.
- ↑ Ромер Д., 2014, с. 75.
- ↑ Palgrave (Newbery), 2018, с. 11172—11178.
- ↑ Spear, Young, 2014.
- ↑ Аджемоглу, 2018, с. 437—445.
- ↑ Туманова, Шагас, 2004, с. 228—229.
- ↑ 13,0 13,1 Аджемоглу, 2018, с. 445.
- ↑ Туманова, Шагас, 2004, с. 187.
- ↑ 15,0 15,1 Туманова, Шагас, 2004, с. 233.
- ↑ Аджемоглу, 2018, с. 36—47.
- ↑ 17,0 17,1 17,2 Аджемоглу, 2018, с. 438.
- ↑ Туманова, Шагас, 2004, с. 229.
- ↑ Аджемоглу, 2018, с. 91.
- ↑ Аджемоглу, 2018, с. 440.
- ↑ 21,0 21,1 Туманова, Шагас, 2004, с. 230.
- ↑ Аджемоглу, 2018, с. 447.
- ↑ Palgrave (Kamihigashi), 2018, с. 13860.
- ↑ Туманова, Шагас, 2004, с. 231.
- ↑ 25,0 25,1 Аджемоглу, 2018, с. 449.
- ↑ Туманова, Шагас, 2004, с. 232.
- ↑ Туманова, Шагас, 2004, с. 230—231.
- ↑ 28,0 28,1 Аджемоглу, 2018, с. 439.
- ↑ 29,0 29,1 29,2 Аджемоглу, 2018, с. 472.
- ↑ 30,0 30,1 Туманова, Шагас, 2004, с. 237.
- ↑ Аджемоглу, 2018, с. 471.
- ↑ Туманова, Шагас, 2004, с. 235.
- ↑ Аджемоглу, 2018, с. 473.
- ↑ Аджемоглу, 2018, с. 461.
- ↑ Туманова, Шагас, 2004, с. 241.
- ↑ Туманова, Шагас, 2004, с. 236—237.
- ↑ Туманова, Шагас, 2004, с. 245—246.
- ↑ 38,0 38,1 Туманова, Шагас, 2004, с. 246.
- ↑ Туманова, Шагас, 2004, с. 247.
- ↑ Туманова, Шагас, 2004, с. 248.
- ↑ Туманова, Шагас, 2004, с. 248—249.
- ↑ 42,0 42,1 Аджемоглу, 2018, с. 484.
- ↑ 43,0 43,1 43,2 Аджемоглу, 2018, с. 485.
- ↑ Аджемоглу, 2018, с. 597—598.
- ↑ Sidrauski, 1967.
- ↑ 46,0 46,1 Аджемоглу, 2018, с. 501.
- ↑ Туманова, Шагас, 2004, с. 252.
- ↑ Туманова, Шагас, 2004, с. 253.
- ↑ Hall, Jones, 1996.
- ↑ De Long, 1988.
- ↑ Romer P. M., 1989.
- ↑ Аджемоглу, 2018, с. 698.
Литература
- Асемоглу Д. Введение в теорию современного экономического роста: в 2 кн. Книга 1 = Introduction to Modern Economic Growth (2009). — М.: Издательский дом «Дело» РАНХиГС, 2018. — 928 с. — ISBN 978-5-7749-1262-9.
- Барро Р. Д., Сала-и-Мартин Х. Экономический рост / Пер. с англ.. — М.: Бином. Лаборатория знаний, 2010. — 824 с. — ISBN 978-5-94774-790-4.
- Бланшар О. Ж., Фишер С. Лекции по макроэкономике = Lectures on macroeconomics. — М.: Издательский дом «Дело» РАНХиГС, 2014. — 680 с. — ISBN 978-5-7749-0829-5.
- Ромер Д. Высшая макроэкономика = Advanced Macroeconomics. — М.: Изд. дом ВШЭ, 2014. — 855 с. — ISBN 978-5-7568-0406-2.
- Туманова Е. А., Шагас Н. Л. Макроэкономика. Элементы продвинутого подхода. — М.: ИНФРА-М, 2004. — 400 с. — ISBN 5-1600-1864-6.
- Cass D.[англ.]. Optimum Growth in an Aggregative Model of Capital Accumulation // The Review of Economic Studies[англ.]. — 1965. — Vol. 32, № 3. — P. 233—240.
- De Long J. B. Productivity Growth, Convergence, and Welfare: Comment // The American Economic Review[англ.]. — 1988. — Vol. 78, № 5. — P. 1138—1154.
- Hall R. E., Jones C. I. The Productivity of Nations // NBER Working Paper. — 1996. — № 5812. — doi:10.3386/w5812.
- Kamihigashi T. Transversality Conditions and Dinamic Economic Behaviour // The New Palgrave Dictionary of Economics / Macmillan Publishers Ltd. — L.: Palgrave Macmillan UK, 2018. — P. 13858—13862. — ISBN 978-1-349-95188-8.
- Koopmans T.C. On the concept of optimal economic growth // Cowles Foundation for Research in Economics, Yale University, Discussion Paper. — 1963. — № 163.
- Koopmans T.C. On the concept of optimal economic growth // Pontificiae Academiae Scientiarum Scripta varia //The Econometric Approach to Development Planning - Part I. — 1965. — Vol. 28. — P. 225—300.
- Newbery D. M.[англ.]. Ramsey Model // The New Palgrave Dictionary of Economics / Macmillan Publishers Ltd. — L.: Palgrave Macmillan UK, 2018. — P. 11172—11178. — ISBN 978-1-349-95188-8.
- Ramsey F. P. A mathematical theory of saving // The Economic Journal[англ.]. — 1928. — Vol. 38, № 152. — P. 543—559.
- Romer P. M. Human Capital And Growth: Theory and Evidence // NBER Working paper. — 1989. — № 3173. — doi:10.3386/w3173.
- Sidrauski M. Rational Choice and Patterns of Growth in a Monetary Economy (англ.) // The American Economic Review[англ.] : journal. — 1967. — Vol. 57, no. 2. — P. 534—544.
- Spear S. E., Young W. Optimum savings and optimal growth: Ramsey — Mavlinvaud — Koopmans nexus // Macroeconomic Dynamics[англ.]. — 2014. — Vol. 18, № 1. — P. 215—243. — doi:10.1017/S1365100513000291.