Корень Бринга

y=Br(x)

В алгебре корень Бринга или ультрарадикал — это аналитическая функция [math]\displaystyle{ Br(a) }[/math], задающая единственный действительный корень многочлена [math]\displaystyle{ x^5+x+a }[/math]. Иначе говоря, для любого [math]\displaystyle{ a }[/math] верно, что

[math]\displaystyle{ Br(a)^5+Br(a)+a=0. }[/math]

Разрез на комплексной плоскости проходит вдоль вещественной полуоси [math]\displaystyle{ x\leqslant -1 }[/math].

Корень Бринга был введён шведским математиком Эрландом Самуэлем Брингом.

Джордж Джеррард показал, что все уравнения 5-й степени могут быть решены в радикалах и корнях Бринга.

Нормальная форма Бринга — Жерара

Если

[math]\displaystyle{ x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5=0 }[/math]

тогда, если

[math]\displaystyle{ y = x^4+b_1x^3+b_2x^2+b_3x+b_4, }[/math]

мы можем получить полином 5-й степени от [math]\displaystyle{ y }[/math], сделав преобразование Чирнгауза, например, используя результант для исключения [math]\displaystyle{ x }[/math]. Мы можем затем подобрать конкретные значения коэффициентов [math]\displaystyle{ b_i }[/math] для того, чтобы получить полином от [math]\displaystyle{ y }[/math] в форме

[math]\displaystyle{ y^5 + py + q }[/math]

Эта неполная форма, открытая Брингом и переоткрытая Жераром, называется нормальной формой Бринга — Жерара. Метод «в лоб» при попытке приведения к нормальной форме Бринга — Жерара не срабатывает; нужно делать это шаг за шагом, применяя несколько преобразований Чирнгауза, которые современные системы аналитических вычислений делают довольно легко.

В начале, подставляя [math]\displaystyle{ x-a_1/5 }[/math] вместо [math]\displaystyle{ x }[/math], избавляемся от члена с [math]\displaystyle{ x^4 }[/math]. Затем, применяя идею Чирнгауза для исключения и члена [math]\displaystyle{ x^3 }[/math], введём переменную [math]\displaystyle{ y = x^2+px+q }[/math] и найдём такие [math]\displaystyle{ p }[/math] и [math]\displaystyle{ q }[/math], чтобы в результате коэффициенты при [math]\displaystyle{ x^3 }[/math] и [math]\displaystyle{ x^4 }[/math] стали равны 0. Конкретнее, подстановки

[math]\displaystyle{ q = \frac{2c}{5} }[/math] и

[math]\displaystyle{ p = \frac{\sqrt{5} \sqrt{12 c^3-40 e c+45 d^2}-15 d}{10 c} }[/math]

исключают члены третьей и четвёртой степени одновременно из

[math]\displaystyle{ x^5 + cx^3 + dx^2 + ex + f }[/math]

Следующим шагом делаем подстановку

[math]\displaystyle{ y = x^4+b_1x^3+b_2x^2+b_3x+b_4 }[/math]

в форму

[math]\displaystyle{ x^5 + dx^2+ex+f }[/math]

и исключаем также член второй степени, в процессе чего не потребуется решения уравнений степени выше 3. При этом выражения для [math]\displaystyle{ b_1, b_2 }[/math] и [math]\displaystyle{ b_4 }[/math] содержат квадратные корни, а в выражении для [math]\displaystyle{ b_3 }[/math] присутствует корень третьей степени.

Общий вид сравнительно легко вычислить с помощью компьютерных систем типа Maple или Mathematica, но он слишком громоздкий, поэтому лучше опишем метод, который затем может быть применён в конкретном случае. В любом частном случае можно составить систему из трёх уравнений для коэффициентов [math]\displaystyle{ b_i }[/math] и решить её. Одно из решений, полученных таким образом, будет включать корни многочленов не выше третьей степени; рассмотрев затем результант с вычисленными коэффициентами, сведём уравнение к форме Бринга — Жерара. Корни первоначального уравнения выражаются через корни полученного уравнения.

Рассматриваемые как алгебраическая функция, решения уравнения

[math]\displaystyle{ x^5+ux+v = 0 }[/math]

зависят от двух параметров, [math]\displaystyle{ u }[/math] и [math]\displaystyle{ v }[/math], однако заменой переменной можно видоизменить уравнение так, чтобы неизвестная была функцией уже только одного параметра. Так, если положить

[math]\displaystyle{ z = {x \over (-u/5)^{1/4}} }[/math]

придём к форме

[math]\displaystyle{ x^5 - 5x - 4t = 0 }[/math]

которая содержит [math]\displaystyle{ x }[/math] как алгебраическую функцию одного комплексного, вообще говоря, параметра [math]\displaystyle{ t }[/math], где [math]\displaystyle{ t=-(v/4)(-u/5)^{-5/4} }[/math].

Корни Бринга

Как функции комплексной переменной t, корни x уравнения

[math]\displaystyle{ x^5 - 5x - 4t = 0 }[/math]

имеют точки ветвления, где дискриминант 800 000(t⁴ - 1) обращается в ноль, то есть в точках 1, −1, а также i и -i. Монодромия вокруг любой из точек ветвления обменивает две из них, оставляя одну на месте. Для вещественных значений t, больших или равных −1, наибольший вещественный корень есть функция от t, монотонно возрастающая от 1; назовём эту функцию корень Бринга, BR(t). Выбирая ветвь, обрезанную вдоль вещественной оси от [math]\displaystyle{ -\infty }[/math] до −1, мы можем продолжить корень Бринга на всю комплексную плоскость, устанавливая значения вдоль ветви так, чтобы получалось аналитическое продолжение вдоль верхней полуплоскости.

Конкретно, положим [math]\displaystyle{ a_0 = 3, a_1 = {1\over100}, a_2 = -{27\over400\,000}, a_3 = {549\over800\,000\,000} }[/math], и последовательность a_i определим рекуррентно

[math]\displaystyle{ a_{n+4} = -{\frac {185\,193}{5\,278\,000}}\,{\frac {2\,n+5}{n+4}}a_{n+3} }[/math]

[math]\displaystyle{ -{\frac {9\,747}{ 52\,780\,000}}\,{\frac {10\,{n}^{2}+40\,n+39}{ \left( n+4 \right) \left( n+3 \right) }}a_{n+2} }[/math]

[math]\displaystyle{ -{\frac {57}{52\,780\,000}}\,{\frac { \left( 2\,n+3 \right) \left( 10\,{n}^{2}+30\,n+17 \right) }{ \left( n+4 \right) \left( n+3 \right) \left( n+2 \right) }}a_{n+1} }[/math]

[math]\displaystyle{ -{\frac {1}{6\,597\,500\,000}}\,{\frac { \left( 5\,n+11 \right) \left( 5\,n+7 \right) \left( 5\,n+3 \right) \left( 5\,n-1 \right) }{ \left( n+4 \right) \left( n+3 \right) \left( n+2 \right) \left( n+1 \right) }}a_n. }[/math]

Для комплексных значений t таких, что |t - 57| < 58, получим

[math]\displaystyle{ \operatorname{BR}(t) = \sum_{n=0}^\infty a_n (t-57)^n, }[/math]

что можно аналитически продолжить, о чём было уже упомянуто.

Корни x⁵ — 5x — 4t = 0 можно теперь выразить в терминах корней Бринга таким образом:

[math]\displaystyle{ r_n = i^{-n} \operatorname{BR}(i^n t) }[/math]

для n от 0 до 3, и

[math]\displaystyle{ r_4 = -r_0-r_1-r_2-r_3 }[/math]

для пятого корня.

Решение общего уравнения пятой степени

Мы можем теперь выразить корни полинома

[math]\displaystyle{ x^5 + px +q=0 }[/math]

в терминах радикалов Бринга как

[math]\displaystyle{ x=\sqrt[4]{p} \cdot BR\left(\frac{q}{\sqrt[4]{p^5}}\right)=\sqrt[4]{p}\cdot H\left(\frac{\sqrt[4]{p}\cdot e^{\frac{2 \pi ik}{5}}}{\sqrt[5]{q}}\right),k=0..4 }[/math]

для подсчёта корня достаточно брать только 1 значение из 4-x [math]\displaystyle{ \sqrt[4]{p} }[/math]

[math]\displaystyle{ BR(x)=H\left(\frac{e^{\frac{2\pi ik}{5}}}{\sqrt[5]{x}}\right),k=0...4 }[/math].

Доказательство

В уравнении [math]\displaystyle{ x^5+px+q=0 }[/math] сделаем подстановку [math]\displaystyle{ x=\alpha y }[/math], получим [math]\displaystyle{ y^5+\frac{p}{\alpha^4}y+\frac{q}{\alpha^5}=0 }[/math]. Возьмём [math]\displaystyle{ \alpha=\sqrt[4]{p} }[/math] , тогда получим: [math]\displaystyle{ y^5+y+\frac{q}{p^{\frac{5}{4}}}=0 }[/math]. Его корни по определению равны :

[math]\displaystyle{ y=BR\left(\frac{q}{p^{\frac{5}{4}}}\right) }[/math], тогда корни исходного уравнения равны

[math]\displaystyle{ x=\sqrt[4]{p}\cdot BR\left(\frac{q}{p\sqrt[4]{p}}\right) }[/math]

Что и требовалось доказать.

Итак, у нас есть сведение к форме Бринга-Жерара в терминах разрешимых полиномиальных уравнений, при этом используются полиномиальные преобразования, включающие выражения в корнях не выше четвёртой степени. Это значит, что преобразования могут быть обращены нахождением корней многочлена, выраженных в радикалах. Эта процедура порождает лишние решения, но если отсечь их численными методами, то получим выражение для корней уравнения пятой степени через квадратные, кубические корни и радикалы Бринга, что т.о. будет алгебраическим решением в терминах алгебраических функций одной переменной - алгебраическим решением общего уравнения пятой степени.

Примеры

1) [math]\displaystyle{ x^5+2x+7=0 }[/math]

[math]\displaystyle{ x=\sqrt[4]{2} \cdot BR \left(\frac{7}{2\sqrt[4]{2}}\right)=\sqrt[4]{2}\cdot H\left(\sqrt[5]{\frac{2\sqrt[4]{2}}{7}}e^{\frac{2\pi ik}{5}}\right),k=0...4 }[/math]

2) [math]\displaystyle{ x^5-x+7=0 }[/math]

[math]\displaystyle{ x=-\sqrt[4]{-1} BR\left(\frac{7}{\sqrt[4]{-1}}\right)=-e^{\frac{\pi i}{4}}\cdot BR\left(\frac{7}{e^{\frac{\pi i}{4}}}\right)=-e^{\frac{\pi i}{4}}\cdot H\left(\frac{e^{\frac{\pi i}{20}}}{\sqrt[5]{7}}e^{\frac{2\pi ik}{5}}\right),k=0...4 }[/math],

функция [math]\displaystyle{ H(x) }[/math] определена ниже

3)[math]\displaystyle{ x^5-\frac{5}{2}x-26=0 }[/math]

[math]\displaystyle{ x_k=e^{\frac{2\pi ik}{5}}\sqrt[5]{\frac{\left(\sqrt{2}+\sqrt{2-\sqrt{2}}\right)^2 \left(-\sqrt{2}+\sqrt{2+\sqrt{2}}\right)}{2}}+e^{\frac{4\pi ik}{5}}\sqrt[5]{\frac{\left(-\sqrt{2}+\sqrt{2+\sqrt{2}}\right)^2 \left(\sqrt{2}-\sqrt{2-\sqrt{2}}\right)}{2}}+ }[/math]

[math]\displaystyle{ +e^{\frac{6\pi ik}{5}}\sqrt[5]{\frac{\left(-\sqrt{2}+\sqrt{2-\sqrt{2}}\right)^2 \left(\sqrt{2}+\sqrt{2-\sqrt{2}}\right)}{2}}+e^{\frac{8\pi ik}{5}}\sqrt[5]{\frac{\left(\sqrt{2}-\sqrt{2-\sqrt{2}}\right)^2 \left(-\sqrt{2}-\sqrt{2+\sqrt{2}}\right)}{2}},k=0,1,2,3,4 }[/math].

4) [math]\displaystyle{ x^5-5x+12=0 }[/math]

[math]\displaystyle{ x_k=-\sqrt[4]{5}\cdot e^{\frac{\pi i}{4}}\cdot BR\left(\frac{2}{5\sqrt[4]{5}\cdot e^{\frac{\pi i}{4}}}\right) }[/math]

[math]\displaystyle{ x_k=5^{-\frac{2}{5}}e^{\frac{2\pi ik}{5}}\sqrt[5]{{\left(\sqrt{5}+\sqrt{5-\sqrt{5}}\right)^2 \left(-\sqrt{5}+\sqrt{5+\sqrt{5}}\right)}}+e^{\frac{4\pi ik}{5}}5^{-\frac{2}{5}}\sqrt[5]{{\left(-\sqrt{5}+\sqrt{5+\sqrt{5}}\right)^2 \left(\sqrt{5}-\sqrt{5-\sqrt{5}}\right)}}+ }[/math]

[math]\displaystyle{ +5^{-\frac{2}{5}}e^{\frac{6\pi ik}{5}}\sqrt[5]{{\left(-\sqrt{5}-\sqrt{5+\sqrt{5}}\right)^2 \left(\sqrt{5}+\sqrt{5-\sqrt{5}}\right)}}+e^{\frac{8\pi ik}{5}}5^{-\frac{2}{5}}\sqrt[5]{{\left(\sqrt{5}-\sqrt{5-\sqrt{5}}\right)^2 \left(-\sqrt{5}-\sqrt{5+\sqrt{5}}\right)}},k=0,1,2,3,4 }[/math]

5) [math]\displaystyle{ x^5+\frac{15-20\sqrt{\pi}}{\pi +1}x-\frac{44+8\sqrt{\pi}}{\pi +1}=0 }[/math]

[math]\displaystyle{ x_k=e^{\frac{2\pi i k}{5}}\sqrt[5]{\frac{\left(\sqrt{\pi +1 }+\sqrt{\pi +1-\sqrt{\pi+1}}\right)^2\left(-\sqrt{\pi +1 }+\sqrt{\pi +1+\sqrt{\pi+1}}\right)}{(\pi+1)^2}}+e^{\frac{4\pi i k}{5}}\sqrt[5]{\frac{\left(-\sqrt{\pi +1 }+\sqrt{\pi +1+\sqrt{\pi+1}}\right)^2\left(+\sqrt{\pi +1 }-\sqrt{\pi +1-\sqrt{\pi+1}}\right)}{(\pi+1)^2}}+ }[/math][math]\displaystyle{ +e^{\frac{6\pi i k}{5}}\sqrt[5]{\frac{\left(-\sqrt{\pi +1 }-\sqrt{\pi +1+\sqrt{\pi+1}}\right)^2\left(+\sqrt{\pi +1 }+\sqrt{\pi +1-\sqrt{\pi+1}}\right)}{(\pi+1)^2}}++e^{\frac{8\pi i k}{5}}\sqrt[5]{\frac{\left(+\sqrt{\pi +1 }-\sqrt{\pi +1-\sqrt{\pi+1}}\right)^2\left(-\sqrt{\pi +1 }-\sqrt{\pi +1+\sqrt{\pi+1}}\right)}{(\pi+1)^2}},k=0,1,2,3,4. }[/math]

6) [math]\displaystyle{ x^5+15x-44=0 }[/math]

[math]\displaystyle{ x_k=e^{\frac{2\pi i}{5}}\sqrt[5]{\sqrt{2}-1}+e^{\frac{4\pi i}{5}}\sqrt[5]{3-2\sqrt{2}}+e^{\frac{6\pi i}{5}}\sqrt[5]{3+2\sqrt{2}}-e^{\frac{8\pi i}{5}}\sqrt[5]{\sqrt{2}+1},k=0,1,2,3,4. }[/math]

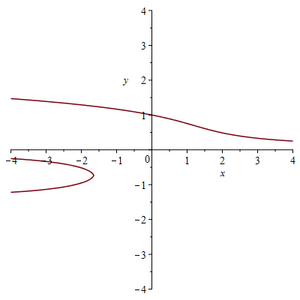
График функции

Для классификации введём дискриминант [math]\displaystyle{ D=256p^5+3125q^4 }[/math]

Тогда в зависимости от знака D тип графика можно разбить на 3 случая:

• 

  [math]\displaystyle{ D\gt 0 }[/math]. 1 действительный корень и 4 комплексных корня. Максимум и минимум (если существуют) находятся по одну сторону от оси OX

• 

  [math]\displaystyle{ D\lt 0 }[/math]. 3 действительных корня и два комплексных. Максимум и минимум находятся по разные стороны от оси OX

• 

  [math]\displaystyle{ D=0 }[/math]. Максимум и минимум (если существуют) находятся по одну сторону от оси OX. Полином имеет кратные корни. Их можно найти по формуле:[math]\displaystyle{ gcd(x^5+px+q,5x^4+p) }[/math], где [math]\displaystyle{ gcd(x,y) }[/math] — наибольший общий делитель.

Если [math]\displaystyle{ \frac{D}{256p^4}=0 }[/math], то уравнение имеет кратные корни.

Разрешимые классы уравнений 5 степени

1) [math]\displaystyle{ x^5+5ax^3+5a^2x+b=0 }[/math]

[math]\displaystyle{ x_k=e^{\frac{2\pi i k}{5}}\sqrt[5]{\frac{\sqrt{b^2+4a^5}-b}{2}}-\frac{a}{e^{\frac{2\pi i k}{5}}\sqrt[5]{\frac{\sqrt{b^2+4a^5}-b}{2}}} }[/math].

2) Если в уравнении [math]\displaystyle{ x^5+ax+b }[/math] , [math]\displaystyle{ a,b\in Q,\exists\varepsilon=\pm1,\exists e\neq0,\exists c\gt 0 }[/math]

[math]\displaystyle{ a=\frac{5e^4(3-4\epsilon c)}{c^2+1},b=\frac{-4e^5(11\epsilon+2c)}{c^2+1}, }[/math] то корни выражаются через:

[math]\displaystyle{ x_j=e(\omega^ju_1+\omega^{2j}u_2+\omega^{3j}u_3+\omega^{4j}u_4),j=0,1,2,3,4 }[/math], где [math]\displaystyle{ \omega=e^{\frac{2\pi i}{5}} }[/math],[math]\displaystyle{ D=c^2+1 }[/math],

[math]\displaystyle{ u_1=\sqrt[5]{\frac{\left(\sqrt{D}+\sqrt{D-\varepsilon\sqrt{D}}\right)^2 \left(-\sqrt{D}+\sqrt{D-\varepsilon\sqrt{D}}\right)}{D^2}} }[/math]

[math]\displaystyle{ u_2=\sqrt[5]{\frac{\left(-\sqrt{D}+\sqrt{D-\varepsilon\sqrt{D}}\right)^2 \left(\sqrt{D}-\sqrt{D-\varepsilon\sqrt{D}}\right)}{D^2}} }[/math]

[math]\displaystyle{ u_3=\sqrt[5]{\frac{\left(-\sqrt{D}-\sqrt{D-\varepsilon\sqrt{D}}\right)^2 \left(\sqrt{D}+\sqrt{D-\varepsilon\sqrt{D}}\right)}{D^2}} }[/math]

[math]\displaystyle{ u_4=\sqrt[5]{\frac{\left(\sqrt{D}-\sqrt{D-\varepsilon\sqrt{D}}\right)^2 \left(-\sqrt{D}-\sqrt{D-\varepsilon\sqrt{D}}\right)}{D^2}} }[/math]

Другие свойства

Много других свойств корней Бринга было получено, первые были сформулированы в терминах модулярных эллиптических функций Шарлем Эрмитом в 1858. Напишем основные свойства:

0.[math]\displaystyle{ \operatorname{BR}(-a)=-\operatorname{BR}(a) }[/math]

1. [math]\displaystyle{ \operatorname{BR}(ia)=i\operatorname{BR}(a) }[/math]
2. [math]\displaystyle{ \operatorname{BR}(a^5+a)=-a }[/math]
3. [math]\displaystyle{ \lim_{n \to \infty}BR(n)=\sqrt[5]{n} }[/math]
4. [math]\displaystyle{ \operatorname{BR}\left(\frac{m^5+mn^4}{n^5}\right)=-\frac{m}{n} }[/math] , как следствие из 2
5. [math]\displaystyle{ BR(x)'=\frac{1}{5BR(x)^4+1} }[/math]
6. [math]\displaystyle{ \int \frac{1}{5BR(x)^4+1}dx=BR(x)+C }[/math]

Разрешимость в радикалах

[math]\displaystyle{ x^5+px+q=0 }[/math]

[math]\displaystyle{ D=256p^5+3125q^4 }[/math]

если [math]\displaystyle{ p=\frac{3125\phi \chi^4}{(\phi-1)^4(\phi^2-6\phi+25)},q=\frac{3125\phi \chi^5}{(\phi-1)^4(\phi^2-6\phi+25)},\phi\in R,\chi\in R }[/math],

то уравнение разрешимо в стандартных радикалах.

Разложение в ряд при [math]\displaystyle{ x\rightarrow\infty }[/math]

Введём: [math]\displaystyle{ Br(x)=H\left(\frac{1}{\sqrt[5]{x}}\right) }[/math], [math]\displaystyle{ y=\frac{1}{\sqrt[5]{x}} }[/math]

Ряд примет вид: [math]\displaystyle{ H(y)=-\frac{1}{y}+\frac{y^3}{5}+\frac{y^7}{5^2}+\frac{y^{11}}{5^3}-\frac{21y^{19}}{5^6}-\frac{78y^{23}}{5^7}-\frac{187y^{27}}{5^8} -\frac{286y^{31}}{5^9}+\frac{9367y^{39}}{5^{12}}+\frac{39767y^{43}}{5^{13}}+\frac{105672y^{47}}{5^{14}}... }[/math]

y=H(x)

[math]\displaystyle{ BR(z)=H\left(\frac{1}{\sqrt[5]{z}}\right)=L\left(\frac{1}{z^{\frac{4}{5}}}\right)\sqrt[5]{z} }[/math]

Тогда:

при [math]\displaystyle{ z\rightarrow\infty }[/math]

[math]\displaystyle{ L(z)=\frac{-1+\displaystyle{\sum_{n=1}^{\infty}(-1)^n \frac{j_n}{z^{5n}}}}{z},j_1=1,j_2=1,j_3=5,j_4=35,... }[/math], где

при [math]\displaystyle{ z\rightarrow0 }[/math]

[math]\displaystyle{ L(z)= \sum_{n=0}^{\infty} - {\frac {{3125}^{-n}\alpha \left( -1/10,2 n \right) \alpha \left( 2/5,2 n \right) \left( -16 \right) ^{n}{z}^{5 n}} {\alpha \left( 4/5,n \right) \alpha \left( 3/5,n \right) \alpha \left( 2/5,n \right) n!}}+1/5 {\frac {{3125}^{-n}\alpha \left( 4/5,2 n \right) \alpha \left( 3/10,2 n \right) \left( -16 \right) ^{n} {z}^{5 n+1}}{\alpha \left( 6/5,n \right) \alpha \left( 4/5,n \right) \alpha \left( 3/5,n \right) n!}}+ }[/math]

[math]\displaystyle{ +1/25 {\frac {{3125}^{-n}\alpha \left( 6/5,2 n \right) \left( -16 \right) ^{n} {z}^{5 n+2}}{\alpha \left( 7/5,n \right) \alpha \left( 6/5,n \right) \alpha \left( 4/5,n \right) n!}\alpha \left( {\frac{7}{10}},2 n \right)+{\frac {{3125}^{-n}\alpha \left( 8/5,2 n \right) \left( -16 \right) ^{n} {z}^{5 n+3}}{125 \alpha \left( 8/5,n \right) \alpha \left( 7/5,n \right) \alpha \left( 6/5,n \right) n!}\alpha \left( {\frac{11}{10}},2 n \right) }} }[/math]

y=L(x)

где [math]\displaystyle{ \alpha(a,b)=\frac{\Gamma(a+b)}{\Gamma(a)} }[/math]

Разложение в ряд при [math]\displaystyle{ x\rightarrow0 }[/math]

[math]\displaystyle{ BR(a)=- \sum_{k=0}^\infty \binom{5k}{k} \frac{(-1)^k a^{4k+1}}{4k+1} = a + a^5 - 5 a^9 + 35 a^{13} - ... }[/math] или

[math]\displaystyle{ \operatorname{BR}(a) = -a \,\,_4F_3\left(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5};\frac{1}{2},\frac{3}{4},\frac{5}{4};-5\left(\frac{5a}{4}\right)^4\right) }[/math]

Частные значения

[math]\displaystyle{ \operatorname{BR}(0)=0 }[/math]

[math]\displaystyle{ \operatorname{BR}(-1)=\frac{\sqrt[3]{100+12\sqrt{69}}}{6}+\frac{2}{3\sqrt[3]{100+12\sqrt{69}}}-\frac{1}{3} }[/math]

[math]\displaystyle{ \operatorname{BR}(2)=-1 }[/math]

Решение через пределы

Дано уравнение: [math]\displaystyle{ x^5-px-q=0 }[/math], его корень можно представить в виде:

[math]\displaystyle{ x=\sqrt[5]{q+p\sqrt[5]{q+p\sqrt[5]{q+...}}} }[/math], или [math]\displaystyle{ x=\lim_{n \to \infty}\overbrace{\sqrt[5]{q+p\sqrt[5]{q+...}} }^{n} }[/math]

Доказательство

[math]\displaystyle{ x=\sqrt[5]{q+p\sqrt[5]{q+p\sqrt[5]{q+...}}} }[/math]

1)Представим эту запись в виде последовательности [math]\displaystyle{ x_n }[/math] , где:

[math]\displaystyle{ x_1=\sqrt[5]{q} }[/math]

[math]\displaystyle{ x_2=\sqrt[5]{q+p\sqrt[5]{q}} }[/math]

[math]\displaystyle{ x_{n+1}=\sqrt[5]{q+px_n} }[/math]

2) Эта последовательность монотонно возрастает и ограничена , значит имеет предел при [math]\displaystyle{ n\rightarrow\infty }[/math], и [math]\displaystyle{ x_{n+1}=x_{n} }[/math],

значит получаем уравнение: [math]\displaystyle{ x=\sqrt[5]{q+px} }[/math], тогда:

[math]\displaystyle{ x^5-px-q=0 }[/math]

Что и требовалось доказать.

Решение через тета функции

[math]\displaystyle{ x^5-x+d=0 }[/math]

1)[math]\displaystyle{ k=\tan\left(\frac{1}{4}\arcsin\left(\frac{16}{25\sqrt{5}d^2}\right)\right) }[/math],[math]\displaystyle{ K(x)=\int\limits_{0}^{\frac{\pi}{2}} \frac{d\varphi}{\sqrt{1-x^2\sin^2\varphi}} }[/math]

[math]\displaystyle{ p_n=i\frac{K(1-k^2)}{K(k^2)}+16n,n=0,1,2,3,4 }[/math] для всех 5 корней

2) Для [math]\displaystyle{ j=0,1,2,3,4 }[/math] определим:

[math]\displaystyle{ S_j=\left(e^{\frac{\pi i }{4}}\right)^j \frac{\sqrt{2}\eta(\tau_j)\eta^2(4\tau_j)}{\eta^3(2\tau_j)},\tau_j=\frac{p_n+2j}{10} }[/math]

[math]\displaystyle{ \eta(x)=e^{\frac{\pi i x}{12}}\prod_{k=1}^\infty(1-e^{2\pi i k x}) }[/math]- Эта-функция Дедекинда

[math]\displaystyle{ S_5=\frac{\sqrt{2}\eta \left(\frac{5p_n}{2}\right)\eta^2(10p_n)}{\eta^3(5p_n)}. }[/math]

Тогда: [math]\displaystyle{ x_n=\frac{\pm1}{2\cdot 5^{\frac{3}{4}}}\cdot \frac{k^{\frac{2}{8}}}{\sqrt{k-k^3}}\cdot(S_0+S_5)(S_1+iS_4)(iS_2+S_3) }[/math], знак выбирается соответственно.

Вывод Глассера

По М. Л. Глассеру (см. ссылку внизу) можно найти решение любого полиномиального уравнения из трёх слагаемых вида:

[math]\displaystyle{ x^N - x + t }[/math]

В частности, произвольное уравнение пятой степени может быть сведено к такой форме с помощью преобразований Чирнхгауза, показанных выше. Возьмём [math]\displaystyle{ x = \zeta^{-1/(N-1)} }[/math], где общая форма:

[math]\displaystyle{ \zeta = e^{2\pi i} + t\phi(\zeta), }[/math]

а

[math]\displaystyle{ \phi(\zeta) = \zeta^{N/(N-1)} }[/math]

Формула Лагранжа показывает, что любая аналитическая функция f в окрестности корня преобразованного общего уравнения относительно ζ может быть выражена в виде бесконечного ряда:

[math]\displaystyle{ f(\zeta) = f(e^{2\pi i}) + \sum^\infty_{n=1} \frac{t^n}{n!}\frac{d^{n-1}}{da^{n-1}}[f'(a)|\phi(a)|^n]_{a = e^{2\pi i}} }[/math]

Если мы положим [math]\displaystyle{ f(\zeta) = \zeta^{-1/(N-1)} }[/math] в этой формуле, то сможем получить корень:

[math]\displaystyle{ x_1 = \exp(-2\pi i/(N -1)) - \frac{t}{N-1}\sum^\infty_{n=0}\frac{(te^{2\pi i/(N-1)})^n}{\Gamma(n + 2)}\frac{\Gamma(\frac{Nn}{N-1} + 1)}{\Gamma(\frac{n}{N-1} + 1)} }[/math]

Следующие N-2 корня могут быть найдены заменой [math]\displaystyle{ \exp(-2\pi i / (N -1)) }[/math] на другие корни (N-1)-й степени из единицы, а последний корень - из теоремы Виета (например, используя тот факт, что сумма всех корней многочлена трёхчленной формы, приведённой выше, равна 1). С помощью теоремы умножения Гаусса вышеуказанный бесконечный ряд может быть разбит в конечную сумму гипергеометрических функций:

[math]\displaystyle{ \psi(q) = (\frac{\omega t}{N-1})^q n^{qN/(N-1)}\frac{\prod^{N-1}_{k=0}\Gamma(\frac{Nq/(N-1) + 1 + k}{N})}{\Gamma(\frac{q}{N-1} + 1)\prod^{N-2}_{k=0}\Gamma(\frac{q+k+2}{N-1})} }[/math]

[math]\displaystyle{ x_1 = \omega^{-1} - \frac{t}{(N-1)^2}\sqrt{\frac{N}{2\pi(N-1)}}\sum^{N-2}_{q=0}\psi(q)_{N+1}F_N \begin{bmatrix} \frac{qN/(N-1)+1}{N}, \ldots, \frac{qN/(N-1) + N}{N}, 1; \\ \frac{q+2}{N-1}, \ldots, \frac{q+N}{N-1}, \frac{q}{N-1}+1; \\ (\frac{t\omega}{N-1})^{N-1}N^N) \end{bmatrix} }[/math]

где [math]\displaystyle{ \omega = \exp(2\pi i/(N-1)) }[/math].

[math]\displaystyle{ {}_{ax^N+bx^2 + c=0,N\equiv 1\pmod{2}} }[/math]

[math]\displaystyle{ {}_{ x_{N}=-\frac{a}{2b}\sqrt{\left(\frac{c}{b}\right)^{N-1}}{}_{N-1}F_{N-2} \begin{bmatrix} \frac{N+1}{2N},\frac{N+3}{2N},\cdots,\frac{N-2}{N},\frac{N-1}{N},\frac{N+1}{N},\frac{N+2}{N},\cdots,\frac{3N-3}{2N},\frac{3N-1}{2N};\\[8pt] \frac{N+1}{2N-4},\frac{N+3}{2N-4},\cdots,\frac{N-4}{N-2},\frac{N-3}{N-2},\frac{N-1}{N-2},\frac{N}{N-2},\cdots,\frac{3N-5}{2N-4},\frac{3}{2};\\[8pt] -\frac{a^2c^{N-2}}{4b^N\left(N-2\right)^{N-2}} \end{bmatrix} +\sqrt{\frac{c}{b}}{\rm{i}}{}_{N-1}F_{N-2} \begin{bmatrix} \frac{1}{2N},\frac{3}{2N},\cdots,\frac{N-4}{2N},\frac{N-2}{2N},\frac{N+2}{2N},\frac{N+4}{2N},\cdots,\frac{2N-3}{2N},\frac{2N-1}{2N};\\[8pt] \frac{3}{2N-4},\frac{5}{2N-4},\cdots,\frac{2N-3}{2N-4};\\[8pt] -\frac{a^2c^{N-2}}{4b^N\left(N-2\right)^{N-2}} \end{bmatrix} } }[/math]

[math]\displaystyle{ {}_{ x_{N-1}=-\frac{a}{2b}\sqrt{\left(\frac{c}{b}\right)^{N-1}}{}_{N-1}F_{N-2} \begin{bmatrix} \frac{N+1}{2N},\frac{N+3}{2N},\cdots,\frac{N-2}{N},\frac{N-1}{N},\frac{N+1}{N},\frac{N+2}{N},\cdots,\frac{3N-3}{2N},\frac{3N-1}{2N};\\[8pt] \frac{N+1}{2N-4},\frac{N+3}{2N-4},\cdots,\frac{N-4}{N-2},\frac{N-3}{N-2},\frac{N-1}{N-2},\frac{N}{N-2},\cdots,\frac{3N-5}{2N-4},\frac{3}{2};\\[8pt] -\frac{a^2c^{N-2}}{4b^N\left(N-2\right)^{N-2}} \end{bmatrix} -\sqrt{\frac{c}{b}}{\rm{i}}{}_{N-1}F_{N-2} \begin{bmatrix} \frac{1}{2N},\frac{3}{2N},\cdots,\frac{N-4}{2N},\frac{N-2}{2N},\frac{N+2}{2N},\frac{N+4}{2N},\cdots,\frac{2N-3}{2N},\frac{2N-1}{2N};\\[8pt] \frac{3}{2N-4},\frac{5}{2N-4},\cdots,\frac{2N-3}{2N-4};\\[8pt] -\frac{a^2c^{N-2}}{4b^N\left(N-2\right)^{N-2}} \end{bmatrix} } }[/math]

[math]\displaystyle{ {}_{ x_n=-e^{\frac{2n\pi{\rm{i}}}{N-2}}\sqrt[N-2]{\frac{b}{a}}{}_{N-1}F_{N-2} \begin{bmatrix} -\frac{1}{N\left(N-2\right)},-\frac{1}{N\left(N-2\right)}+\frac{1}{N},-\frac{1}{N\left(N-2\right)}+\frac{2}{N},\cdots,-\frac{1}{N\left(N-2\right)}+\frac{1}{N},\frac{N-5}{2N},-\frac{1}{N\left(N-2\right)}+\frac{N-3}{2N},-\frac{1}{N\left(N-2\right)}+\frac{N+1}{2N},-\frac{1}{N\left(N-2\right)}+\frac{N+3}{2N},\cdots,-\frac{1}{N\left(N-2\right)}+\frac{N-1}{N},;\\[8pt] \frac{1}{N-2},\frac{2}{N-2},\cdots,\frac{2N-5}{2N-4},;\\[8pt] -\frac{a^2c^{N-2}}{4b^N\left(N-2\right)^{N-2}} \end{bmatrix} +\sqrt[N-2]{\frac{b}{a}}\sum^{N-3}_{q=1}\frac{\Gamma\left(\frac{2q-1}{N-2}+q\right)}{\Gamma\left(\frac{2q-1}{N-2}+1\right)}\cdot\left(-\frac{c}{b}\sqrt[N-2]{\frac{a^2}{b^2}}\right)^q\cdot\frac{e^{\frac{2n\left(1-2q\right)}{N-2}\pi{\rm{i}}}}{q!}{}_{N-1}F_{N-2} \begin{bmatrix} \frac{Nq-1}{N\left(N-2\right)},\frac{Nq-1}{N\left(N-2\right)}+\frac{1}{N},\frac{Nq-1}{N\left(N-2\right)}+\frac{2}{N},\cdots,\frac{Nq-1}{N\left(N-2\right)}+\frac{N-3}{2N},\frac{Nq-1}{N\left(N-2\right)}+\frac{N+1}{2N},\cdots,\frac{Nq-1}{N\left(N-2\right)}+\frac{N-1}{N};\\[8pt] \frac{q+1}{N-2},\frac{q+2}{N-2},\cdots,\frac{N-4}{N-2},\frac{N-3}{N-2},\frac{N-1}{N-2},\frac{N}{N-2},\cdots,\frac{q+N-2}{N-2},\frac{2q+2N-5}{2N-4};\\[8pt] -\frac{a^2c^{N-2}}{4b^N\left(N-2\right)^{N-2}} \end{bmatrix},n=1,2,\cdots,N-2 } }[/math]

Корни уравнения тогда можно представить как сумму самое большее N-1 гипергеометрических функций. Применяя этот метод к редуцированной форме Бринга-Жеррара, определим следующие функции:

[math]\displaystyle{ \begin{matrix} F_1(t) & = & F_2(t)\\ F_2(t) & = & \,_4F_3(1/5, & 2/5, & 3/5, & 4/5; & 1/2, & 3/4, & 5/4; & 3125t^4/256)\\ F_3(t) & = & \,_4F_3(9/20, & 13/20, & 17/20, & 21/20; & 3/4, & 5/4, & 3/2; & 3125t^4/256)\\ F_4(t) & = & \,_4F_3(7/10, & 9/10 , & 11/10, & 13/10; & 5/4, & 3/2, & 7/4; & 3125t^4/256) \end{matrix} }[/math]

которые суть гипергеометрические функции, присутствующие в рядах выше. Корни уравнения пятой степени тогда:

[math]\displaystyle{ \begin{matrix} x_1 & = & -t^4F_1(t) \\ x_2 & = & -F_1(t) & + \frac{1}{4}tF_2(t) & + \frac{5}{32}t^2F_3(t) & + \frac{5}{32}t^3F_3(t)\\ x_3 & = & -F_1(t) & + \frac{1}{4}tF_2(t) & - \frac{5}{32}t^2F_3(t) & + \frac{5}{32}t^3F_3(t)\\ x_4 & = & -iF_1(t) & + \frac{1}{4}tF_2(t) & - \frac{5}{32}it^2F_3(t) & - \frac{5}{32}t^3F_3(t)\\ x_5 & = & iF_1(t) & + \frac{1}{4}tF_2(t) & + \frac{5}{32}it^2F_3(t) & - \frac{5}{32}t^3F_3(t)\\ \end{matrix} }[/math]

Это по существу тот же результат, что был получен методом дифференциальной резольвенты, разработанным Джеймсом Коклом} и Робертом Харлеем в 1860 году.

Дифференциальная резольвента

[math]\displaystyle{ f[\phi(a)] = 0 }[/math]

Функция φ может быть определена так:

[math]\displaystyle{ \begin{align} \frac{d f[\phi(a)]}{da} = 0 \\[6pt] \frac{d^2 f[\phi(a)]}{da^2} = 0 \\[6pt] \frac{d^3 f[\phi(a)]}{da^3} = 0 \\[6pt] \frac{d^4 f[\phi(a)]}{da^4} = 0 \end{align} }[/math]

Тогда дифференциальная резольвента такова:

[math]\displaystyle{ \frac{(256 - 3125a^4)}{1155}\frac{d^4\phi}{da^4} - \frac{6250a^3}{231}\frac{d^3\phi}{da^3} - \frac{4875a^2}{77}\frac{d^2\phi}{da^2} - \frac{2125a}{77}\frac{d\phi}{da} + \phi = 0 }[/math]

См. также

• Теория уравнений

Внешние ссылки

• M.L. Glasser. The Quadratic Formula Made Hard: A Less Radical Approach to Solving Equations. Статья доступна на arXiv.org здесь (недоступная ссылка)
• A.V. Gruzdov, S.V. Berezin. Absolute ultraradical.