Граф гиперкуба
| Граф гиперкуба | |
|---|---|
 | |
| Вершин | 2n |
| Рёбер | 2n−1n |
| Диаметр | n |
| Обхват | 4 if n≥2 |
| Автоморфизмы | n! 2n |
| Хроматическое число | 2 |
| Спектр | [math]\displaystyle{ \{(n - 2 k)^{\binom{n}{k}}; k = 0, \ldots, n\} }[/math] |
| Свойства |
Симметричный
двудольный |
| Обозначение | Qn |
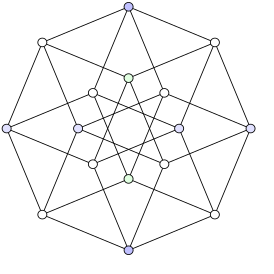
В теории графов графом гиперкуба Qn называется регулярный граф с 2n вершинами, 2n−1n рёбрами и n рёбрами, сходящимися в одной вершине. Его можно получить как одномерный скелет геометрического гиперкуба. Например, Q3 — это граф, образованный 8 вершинами и 12 рёбрами трёхмерного куба. Граф можно получить другим образом, отталкиваясь от семейства подмножеств множества с n элементами путём использования в качестве вершин все подмножества и соединением двух вершин ребром, если соответствующие множества отличаются только одним элементом.
Графы гиперкубов не следует путать с кубическими графами, в которых в каждую вершину сходится ровно три ребра. Единственный гиперкуб, граф которого кубический — это Q3.
Построение

Граф гиперкуба Qn можно построить из семейства подмножеств множества с n элементами путём использования в качестве вершин все подмножества и соединением двух вершин ребром, если соответствующие множества отличаются только одним элементом. Также граф можно построить, используя 2n вершин, пометив их n-битными двоичными числами и соединив пары вершин рёбрами, если расстояние Хэмминга между соответствующими им метками равно 1. Эти два построения тесно связаны — двоичные числа можно представлять как множества (множество позиций, где стоит единица), и два таких множества отличаются одним элементом, если расстояние Хэмминга между соответствующими двумя двоичными числами равно 1.
Qn+1 можно построить из несвязного объединения двух гиперкубов Qn путём добавления рёбер от каждой вершины одной копии Qn до соответствующей вершины другой копии, как показано на рисунке. Соединяющие рёбра образуют паросочетание.
Ещё одно определение Qn — прямое произведение n полных графов K2, содержащих две вершины.
Примеры
Граф Q0 состоит из единственной вершины, граф Q1 является полным графом с двумя вершинами, а Q2 — цикл длины 4.
Граф Q3 — это 1-скелет[англ.] куба, планарный граф с восемью вершинами и двенадцатью рёбрами.
Граф Q4 — это граф Леви конфигурации Мёбиуса.
Свойства
Двудольность
Все графы гиперкубов являются двудольными — их вершины можно раскрасить только двумя цветами. Два цвета этой раскраски можно найти из построения подмножеств графов гиперкубов путём присвоения одного цвета подмножествам, имеющим чётное число элементов и другого цвета подмножествам, имеющим нечётное число элементов.
Гамильтоновы циклы
Любой гиперкуб Qn с n > 1 имеет гамильтонов цикл, проходящий через каждую вершину ровно один раз. Вдобавок, гамильтонов путь между вершинами u, v существует тогда и только тогда, когда u и v имеют различные цвета в двухцветной раскраске графа. Оба факта легко проверить по индукции по размерности гиперграфа с построением графа гиперкуба путём соединения двух меньших гиперкубов.
Вышеописанные свойства гиперкуба тесно связаны с теорией кодов Грея. Более точно, существует биективное соответствие между множеством n-битных циклических кодов Грея и множеством гамильтоновых циклов в гиперкубе Qn.[1] Аналогичное свойство имеет место для ацикличных n-битных кодов Грея и гамильтоновых путей.
Меньше известен факт, что любое совершенное паросочетание в гиперкубе можно расширить до гамильтонова цикла.[2] Вопрос, можно ли любое паросочетание расширить до гамильтонова цикла, остаётся открытым.[3]
Другие свойства
Граф гиперкуба Qn (n > 1) :
- является диаграммой Хассе конечной булевой алгебры;
- является медианным графом. Любой медианный граф является изометричным подграфом гиперкуба и может быть образован путём усечения гиперкуба;
- имеет более чем 22n-2 совершенных паросочетаний (это другое следствие, следующее из индуктивного построения);
- является транзитивным относительно дуг и симметричным. Симметрии графов гиперкубов можно представить как знаковые перестановки, группа автоморфизмов изоморфна [math]\displaystyle{ S_n\wr\Z_2 }[/math];
- содержит все циклы длины 4, 6, …, 2n и поэтому является бипанциклическим графом;
- может быть нарисован как граф единичных расстояний на евклидовой плоскости путём выбора единичного вектора для каждого элемента множества и размещения каждой вершины, соответствующей множеству S, в точке, соответствующей сумме векторов из S;
- является вершинно n-связным графом по теореме Балинского;
- является планарным (может быть нарисован без пересечений) в том и только в том случае, когда n ≤ 3. Для больших значений n гиперкуб имеет род [math]\displaystyle{ (n-4)2^{n-3}+1 }[/math][4][5];
- имеет в точности [math]\displaystyle{ 2^{2^n-n-1}\prod_{k=2}^n k^{{n\choose k}} }[/math] остовных дерева[5];
- семейство Qn (n > 1) является семейством графов Леви[англ.];
- известно, что ахроматическое число графа Qn пропорционально [math]\displaystyle{ \sqrt{n2^n} }[/math], но точная константа пропорциональности неизвестна[6];
- ширина полосы[англ.] графа Qn в точности равна [math]\displaystyle{ \sum_{i=0}^n \binom{n}{\lfloor n/2\rfloor} }[/math].[7];
- собственные значения матрицы инцидентности равны (-n,-n+2,-n+4,…,n-4,n-2,n), а собственные значения матрицы Кирхгофа графа равны (0,2,…,2n);
- изопериметрическое число равно h(G)=1.
Задачи
Задача поиска самого длинного пути или цикла, являющегося порождённым подграфом заданного графа гиперкуба, известна как задача о змее в коробке.
Гипотеза Шиманского[англ.] касается пригодности гиперкуба в качестве сетевой топологии обмена данными. Гипотеза утверждает, что как бы ни переставляли вершины графа, всегда существуют такие (направленные) пути, соединяющие вершины с их образами, что никакие два пути, соединяющие разные вершины, не проходят по одному и тому же ребру в том же направлении[8].
См. также
- Кубически соединённые циклы[англ.]
- Куб Фибоначчи
- Сложенный граф куба[англ.]
- Уполовиненный граф куба[англ.]
Примечания
- ↑ Mills. Some complete cycles on the n-cube // Proceedings of the American Mathematical Society. — American Mathematical Society, 1963. — Т. 14, вып. 4. — С. 640–643. — doi:10.2307/2034292. — ..
- ↑ Perfect matchings extend to Hamiltonian cycles in hypercubes // Journal of Combinatorial Theory, Series B. — 2007. — Т. 97. — С. 1074–1076. — doi:10.1016/j.jctb.2007.02.007..
- ↑ Ruskey, F. and Savage, C. Matchings extend to Hamiltonian cycles in hypercubes Архивная копия от 6 мая 2021 на Wayback Machine on Open Problem Garden. 2007.
- ↑ G. Ringel. ber drei kombinatorische Probleme am n-dimensionalen Wiirfel und Wiirfelgitter // Abh. Math. Sere. Univ. Hamburg. — 1955. — Т. 20. — С. 10-19.
- ↑ 5,0 5,1 Frank Harary, John P. Hayes, Horng-Jyh Wu. A survey of the theory of hypercube graphs // Computers & Mathematics with Applications. — 1988. — Т. 15, вып. 4. — С. 277–289. — doi:10.1016/0898-1221(88)90213-1..
- ↑ Y. Roichman. On the Achromatic Number of Hypercubes // Journal of Combinatorial Theory, Series B. — 2000. — Т. 79, вып. 2. — С. 177–182. — doi:10.1006/jctb.2000.1955..
- ↑ Optimal Numberings and Isoperimetric Problems on Graphs, L.H. Harper, Journal of Combinatorial Theory, 1, 385—393, doi:10.1016/S0021-9800(66)80059-5
- ↑ Ted H. Szymanski. Proc. Internat. Conf. on Parallel Processing. — Silver Spring, MD: IEEE Computer Society Press, 1989. — Т. 1. — С. 103–110..
Ссылки
- F. Harary, J. P. Hayes, H.-J. Wu. A survey of the theory of hypercube graphs // Computers & Mathematics with Applications. — 1988. — Т. 15, вып. 4. — С. 277–289. — doi:10.1016/0898-1221(88)90213-1..
