Регулярный граф
Регуля́рный (одноро́дный) граф — граф, степени всех вершин которого равны, то есть каждая вершина имеет одинаковое количество соседей. Степень регулярности является инвариантом графа и обозначается [math]\displaystyle{ r(G) }[/math]. Для нерегулярных графов [math]\displaystyle{ r(G) }[/math] не определено. Регулярные графы представляют особую сложность для многих алгоритмов.
Регулярный граф с вершинами степени [math]\displaystyle{ k }[/math] называется регулярным графом степени [math]\displaystyle{ k }[/math], или [math]\displaystyle{ k }[/math]‑регулярным.
Регулярные графы степени не больше двух легко классифицировать: 0-регулярный граф состоит из изолированных вершин (нуль-граф), 1-регулярный — из изолированных рёбер, а 2-регулярный — из разрозненных циклов.
3-регулярный граф известен также как кубический.
Сильно регулярный граф есть регулярный граф, для которого существуют такие [math]\displaystyle{ \lambda }[/math] и [math]\displaystyle{ \mu }[/math], что любые две смежные вершины имеют [math]\displaystyle{ \lambda }[/math] общих соседей и любые две несмежные вершины имеют [math]\displaystyle{ \mu }[/math] общих соседей. Наименьшие графы, которые регулярны, но не сильно регулярны — циклический граф и циркулянтный граф на шести вершинах.
Полный граф [math]\displaystyle{ K_m }[/math] является сильно регулярным для любого [math]\displaystyle{ m }[/math].
Теорема Нэш-Вильямса[англ.] гласит, что каждый k‑регулярный граф на 2k + 1 вершинах имеет гамильтонов цикл.
-
0-регулярный граф
-
1-регулярный граф
-
2-регулярный граф
-
3-регулярный граф
-
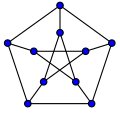
Ещё один 3-регулярный граф — граф Петерсена
Алгебраические свойства
Пусть A есть матрица смежности графа. Тогда граф регулярен тогда и только тогда, когда [math]\displaystyle{ \textbf{j}=(1, \dots ,1) }[/math] есть собственный вектор A[1]. Его собственное число будет постоянной степенью графа. Собственные вектора, соответствующие другим собственным числам, ортогональны [math]\displaystyle{ \textbf{j} }[/math], поэтому для собственных векторов [math]\displaystyle{ v=(v_1,\dots,v_n) }[/math] мы имеем [math]\displaystyle{ \sum_{i=1}^n v_i = 0 }[/math].
Регулярный граф степени k связен тогда и только тогда, когда собственное число k имеет единичную кратность[1].
Другой критерий регулярности и связности графа: граф связен и регулярен тогда и только тогда, когда матрица J с [math]\displaystyle{ J_{ij}=1 }[/math] находится в алгебре смежности[англ.] графа[2].
Пусть G есть k-регулярный граф диаметра D и с собственными числами матрицы смежности [math]\displaystyle{ k=\lambda_0 \gt \lambda_1\geq \dots\geq\lambda_{n-1} }[/math]. Если G не двудолен:
[math]\displaystyle{ D\leq \frac{\log{(n-1)}}{\log(k/\lambda)}+1 }[/math][3] [4]
где
[math]\displaystyle{ \lambda=\max_{i\gt 0}\{|\lambda_i|\} }[/math].
Генерация
Регулярный граф можно сгенерировать программой GenReg.[5]
См. также
- Случайный регулярный граф (англ.)
- Сильно регулярный граф
- Граф Мура (англ.)
- Клетка
Примечания
- ↑ 1,0 1,1 Д. М. Цветкович, М. Дуб и Х. Сачс, «Спектр графов: теория и применение», 3-я редакция, Нью-Йорк: Уайли, 1998.
- ↑ Curtin, Brian (2005), Algebraic characterizations of graph regularity conditions, Designs, Codes and Cryptography Т. 34 (2-3): 241–248, DOI 10.1007/s10623-004-4857-4
- ↑ Gregory Quenell. Spectral diameter estimates for k-regular graphs.
- ↑ Fan R.K. Chung. Spectral Graph Theory. — American Mathematical Society, 1997. — (CBMS). — ISBN 0821803158.
- ↑ М. Мерингер, "Теория графов", 1999, 30, 137.
Ссылки
- Weisstein, Eric W. Regular Graph (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Strongly Regular Graph (англ.) на сайте Wolfram MathWorld.
- GenReg программа и данные Маркуса Мерингера.
- Nash-Williams, Crispin (1969), Valency Sequences which force graphs to have Hamiltonian Circuits, University of Waterloo Research Report, Waterloo, Ontario: University of Waterloo