Остовное дерево
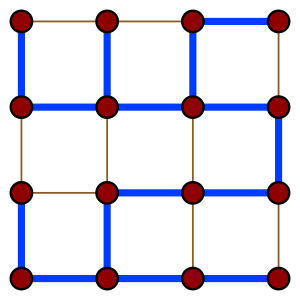
О́стовное де́рево графа (англ. Spanning tree) — это дерево, подграф данного графа, с тем же числом вершин, что и у исходного графа. Неформально говоря, остовное дерево получается из исходного графа удалением максимального числа рёбер, входящих в циклы, но без нарушения связности графа. Остовное дерево включает в себя все [math]\displaystyle{ n }[/math] вершин исходного графа и содержит [math]\displaystyle{ n - 1 }[/math] ребро.
Определение
Остовное дерево — ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины.
Понятие остовный лес неоднозначно, под ним могут понимать один из следующих подграфов:
- любой ациклический подграф, в который входят все вершины графа, но не обязательно связный;
- в несвязном графе — подграф, состоящий из объединения остовных деревьев для каждой его компоненты связности.
Остовное дерево также иногда называют покрывающим деревом, остовом или скелетом графа. Ударение в слове «остовный» у разных авторов указывается на первый (от слова о́стов) или на второй слог.
Свойства
- Любое остовное дерево в графе с [math]\displaystyle{ n }[/math] вершинами содержит ровно [math]\displaystyle{ n - 1 }[/math] ребро.
- Число остовных деревьев в полном графе на [math]\displaystyle{ n }[/math] вершинах равно [math]\displaystyle{ n^{n-2}; }[/math] это утверждение называется формулой Кэли[1]:
- Число остовных деревьев в полном двудольном графе [math]\displaystyle{ K_{m,n} }[/math] равно [math]\displaystyle{ m^{n-1}\cdot n^{m-1}. }[/math]
- В общем случае, число остовных деревьев в произвольном графе может быть вычислено при помощи так называемой матричной теоремы о деревьях.
- Пусть [math]\displaystyle{ \rho }[/math] есть ребро в графе [math]\displaystyle{ \Gamma. }[/math] Обозначим через [math]\displaystyle{ \Gamma\backslash\rho }[/math] граф, полученный из [math]\displaystyle{ \Gamma }[/math] выбрасыванием ребра [math]\displaystyle{ \rho, }[/math] и через [math]\displaystyle{ \Gamma/\rho }[/math] граф, полученный из [math]\displaystyle{ \Gamma }[/math] стягиванием ребра [math]\displaystyle{ \rho }[/math] в точку. Если ребро [math]\displaystyle{ \rho }[/math] не является петлёй в [math]\displaystyle{ \Gamma, }[/math] тогда выполняется следующее соотношение, называемое удаление-плюс-стягивание[2]:
- [math]\displaystyle{ \tau(\Gamma)=\tau(\Gamma\backslash\rho)+\tau(\Gamma/\rho), }[/math]
- где [math]\displaystyle{ \tau(\Gamma) }[/math] обозначает число остовных деревьев в графе [math]\displaystyle{ \Gamma. }[/math]
Алгоритмы
Остовное дерево может быть построено практически любым алгоритмом обхода графа, например поиском в глубину или поиском в ширину. Оно состоит из всех пар рёбер [math]\displaystyle{ (u, v), }[/math] таких, что алгоритм, просматривая вершину [math]\displaystyle{ u, }[/math] обнаруживает в её списке смежности новую, не обнаруженную ранее вершину [math]\displaystyle{ v. }[/math]
Остовные деревья, построенные при обходе графа из вершины [math]\displaystyle{ s }[/math] алгоритмом Дейкстры, обладают тем свойством, что кратчайший путь в графе из [math]\displaystyle{ s }[/math] до любой другой вершины — это (он же единственный) путь из [math]\displaystyle{ s }[/math] до этой вершины в построенном остовном дереве.
Существует также несколько параллельных и распределённых алгоритмов нахождения остовного дерева. Как практический пример распределённого алгоритма можно привести протокол STP.
Если каждому ребру графа присвоен вес (длина, стоимость и т. п.), то нахождением оптимального остовного дерева, которое минимизирует сумму весов входящих в него рёбер, занимаются многочисленные алгоритмы нахождения минимального остовного дерева.
Задача о нахождении остовного дерева, в котором степень каждой вершины не превышает некоторой наперёд заданной константы [math]\displaystyle{ k, }[/math], является NP-полной[3].
Выделение остовного дерева и подсчет числа удалённых рёбер в графах электрических цепей используется для вычисления количества независимых контуров при анализе электрической цепи методом контурных токов[4].
См. также
- Матричная теорема о деревьях
- Минимальное остовное дерево
- Теорема Кэли о числе деревьев
- STP — канальный протокол.
Примечания
- ↑ Martin Aigner, Günter M. Ziegler. Proofs from the book. — Springer-Verlag, 2004. — P. 173—178. — ISBN 978-3540404606.
- ↑ Петрунин А. Сколько деревьев в графе // Квант. — 2018. — № 9. — С. 9—13. — doi:10.4213/kvant20180902.
- ↑ Michael R. Garey, David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. — W.H. Freeman, 1979. — С. 206. — ISBN 0-7167-1045-5.
- ↑ Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — М.: Гардарики, 2002. — 638 с. — ISBN 5-8297-0026-3.