Закон Бернулли

Зако́н Берну́лли[1] (также уравне́ние Берну́лли[2][3], теоре́ма Берну́лли[4][5] или интегра́л Берну́лли[2][6][7]) устанавливает зависимость между скоростью стационарного потока жидкости и её давлением. Согласно этому закону, если вдоль линии тока давление жидкости повышается, то скорость течения убывает, и наоборот. Количественное выражение закона в виде интеграла Бернулли является результатом интегрирования уравнений гидродинамики идеальной жидкости[2] (то есть без вязкости и теплопроводности).
История
Для случая несжимаемой жидкости результат, эквивалентный современному уравнению Бернулли, был опубликован в 1738 году Даниилом Бернулли[K 1]. В современном виде интеграл был опубликован Иоганном Бернулли в 1743 году[11] для случая несжимаемой жидкости, а для некоторых случаев течений сжимаемой жидкости — Эйлером в 1757 году[12].
Интеграл Бернулли в несжимаемой жидкости
| Полное давление | |
|---|---|
| Размерность | [math]\displaystyle{ L^{-1}MT^{-2} }[/math] |
| Единицы измерения | |
| СИ | Дж/м3 = Па |
| СГС | эрг/см3 |
| Примечания | |
| Постоянно вдоль линии тока стационарного течения несжимаемой жидкости. | |
Для стационарного течения несжимаемой жидкости уравнение Бернулли может быть получено как следствие закона сохранения энергии. Закон Бернулли утверждает, что величина [math]\displaystyle{ \rho v^2/2 + \rho g h+ p }[/math] сохраняет постоянное значение вдоль линии тока:
- [math]\displaystyle{ \frac{\rho v^2}{2} + \rho g h+ p = \text{const}. }[/math]
Здесь
- [math]\displaystyle{ \rho }[/math] — плотность жидкости;
- [math]\displaystyle{ v }[/math] — скорость потока;
- [math]\displaystyle{ h }[/math] — высота;
- [math]\displaystyle{ p }[/math] — давление;
- [math]\displaystyle{ g }[/math] — ускорение свободного падения.

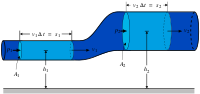
Элементарный вывод уравнения Бернулли из закона сохранения энергии приведён, например, в учебнике Д. В. Сивухина[13]. Рассматривается стационарное движение жидкости вдоль линии тока, изображённое на рисунке. Слева на объем жидкости, первоначально заключённый между двумя сечениями [math]\displaystyle{ A_1 }[/math] и [math]\displaystyle{ A_2 }[/math], действует сила [math]\displaystyle{ F_1=p_1A_1 }[/math], а справа — противоположного направления сила [math]\displaystyle{ F_2=-p_2A_2 }[/math]. Скорость [math]\displaystyle{ v }[/math] и давление [math]\displaystyle{ p }[/math] в сечениях 1 и 2, а также их площади обозначены нижними индексами 1 и 2. За бесконечно малое время [math]\displaystyle{ \Delta t }[/math] левая граница этого объёма жидкости сместилась на малое расстояние [math]\displaystyle{ s_1=v_1\Delta t }[/math], а правая — на расстояние [math]\displaystyle{ s_2=v_2\Delta t }[/math]. Работа, совершённая силами давления, равна:
[math]\displaystyle{ W=F_1s_1+F_2s_2=\Delta t\left(v_1A_1p_1-v_2A_2p_2\right). }[/math]
В начале интервала времени [math]\displaystyle{ \Delta t }[/math] объем жидкости, заключённый между двумя поверхностями [math]\displaystyle{ A_1 }[/math] и [math]\displaystyle{ A_2 }[/math], состоит из левого голубого элемента и средней синей части, в конце этого интервала сместившийся объём состоит из средней синей части и правого голубого элемента. Так как течение стационарное, вклад синего фрагмента в энергию и массу обсуждаемого объёма жидкости не меняется, а сохранение массы позволяет заключить, что масса левого голубого элемента равна массе правого голубого элемента: [math]\displaystyle{ \Delta m=\Delta t v_1A_1\rho_1=\Delta t v_2A_2\rho_2. }[/math] Поэтому работа сил, выражение для которой можно преобразовать к виду: [math]\displaystyle{ \Delta W=\Delta m\left(\frac{p_1}{\rho_1}-\frac{p_2}{\rho_2}\right), }[/math] равна изменению энергии, равному, в свою очередь, разности энергий правого голубого элемента [math]\displaystyle{ \Delta E_2 }[/math] и левого голубого элемента [math]\displaystyle{ \Delta E_1 }[/math].
Для несжимаемой жидкости можно, во-первых, в выражении для работы положить [math]\displaystyle{ \rho_1=\rho_2=\rho }[/math] и, во-вторых, в выражении для энергии элемента жидкости ограничиться кинетической и потенциальной энергией: [math]\displaystyle{ \Delta E_1=\Delta m\left(\frac{v^2_1}2+gh_1\right), }[/math] [math]\displaystyle{ \Delta E_2=\Delta m\left(\frac{v^2_2}2+gh_2\right). }[/math] После этого равенство [math]\displaystyle{ \Delta W=\Delta E_2-\Delta E_1 }[/math] даёт: [math]\displaystyle{ p_1+\rho g h_1+\frac{\rho v_1^2}2 = p_2+\rho g h_2+\frac{\rho v_2^2}2 }[/math], или [math]\displaystyle{ p+\rho g h+\frac{\rho v^2}2={\rm const} }[/math].
Константа в правой части (может различаться для различных линий тока) иногда называется полным давлением[2]. Могут также использоваться термины «весовое давление» [math]\displaystyle{ \rho g h }[/math], «статическое давление» [math]\displaystyle{ p }[/math] и «динамическое давление» [math]\displaystyle{ \rho v^2/2 }[/math]. По словам Д. В. Сивухина[13], нерациональность этих понятий отмечалась многими физиками.
Размерность всех слагаемых — единица энергии на единицу объёма. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Третье слагаемое по своему происхождению является работой сил давления (см. приведённый выше вывод уравнения Бернулли), но в гидравлике может называться «энергией давления» и частью потенциальной энергии[14]).
Вывод формулы Торричелли из закона Бернулли

В применении к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда закон Бернулли даёт равенство полных давлений на свободной поверхности жидкости и на выходе из отверстия:
- [math]\displaystyle{ \rho g h + p_0 = \frac{\rho v^2}{2} + p_0, }[/math]
где
- [math]\displaystyle{ h }[/math] — высота столба жидкости в сосуде, отсчитанная от уровня отверстия,
- [math]\displaystyle{ v }[/math] — скорость истечения жидкости,
- [math]\displaystyle{ p_0 }[/math] — атмосферное давление.
Отсюда: [math]\displaystyle{ v = \sqrt{2gh} }[/math]. Это — формула Торричелли. Она показывает, что при истечении жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты [math]\displaystyle{ h }[/math]. Или, если истекающую из малого отверстия в сосуде струю направить вверх, в верхней точке (в пренебрежении потерями) струя достигнет уровня свободной поверхности в сосуде[15].
Другие проявления и применения закона Бернулли

Приближение несжимаемой жидкости, а с ним и закон Бернулли справедливы и для ламинарных течений газа, если только скорости течения малы по сравнению со скоростью звука[16].
Вдоль горизонтальной трубы координата [math]\displaystyle{ z }[/math] постоянна и уравнение Бернулли принимает вид [math]\displaystyle{ \frac{\rho v^2}{2} + p = \text{const} }[/math]. Отсюда следует, что при уменьшении сечения потока из-за возрастания скорости давление падает. Эффект понижения давления при увеличении скорости потока лежит в основе работы расходомера Вентури[17] и струйного насоса[1].
Закон Бернулли объясняет, почему суда, движущиеся параллельным курсом, могут притягиваться друг к другу (например, такой инцидент произошёл с лайнером «Олимпик»)[18].
Применение в гидравлике
Последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики. Для технических приложений часто уравнение Бернулли записывается в виде, в котором все члены разделены на «удельный вес» [math]\displaystyle{ \rho g }[/math]:
- [math]\displaystyle{ H = h + \frac{p}{\rho g} + \frac{v^2}{2g} = \text{const}, }[/math]
где имеющие размерность длины члены в этом уравнении могут иметь следующие названия:
| Напор[19] | |
|---|---|
| Размерность | [math]\displaystyle{ L }[/math] |
| Единицы измерения | |
| СИ | метр |
| Примечания | |
| Полное давление, делённое на удельный вес. | |
- [math]\displaystyle{ H }[/math] — гидравлическая высота[4] или напор[19],
- [math]\displaystyle{ h }[/math] — нивелирная высота[4],
- [math]\displaystyle{ \frac{p}{\rho g} }[/math] — пьезометрическая высота[4] или (в сумме с нивелирной высотой) гидростатический напор[19],
- [math]\displaystyle{ \frac{v^2}{2g} }[/math] — скоростная высота[4] или скоростной напор[19].
Закон Бернулли справедлив только для идеальных жидкостей, в которых отсутствуют потери на вязкое трение. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, приближённо учитывающих различные «гидравлические потери напора»[19].
Интеграл Бернулли в баротропных течениях
Уравнение Бернулли может быть выведено и из уравнения движения жидкости[K 2][K 3]. При этом течение предполагается стационарным и баротропным. Последнее означает, что плотность жидкости или газа не обязательно постоянна (как у предполагавшейся ранее несжимаемой жидкости), но является функцией только давления: [math]\displaystyle{ \rho=\rho(p) }[/math], что позволяет ввести функцию давления[22] [math]\displaystyle{ \mathcal P = \int{\frac{\mathrm{d}p}{\rho(p)}}. }[/math] В этих предположениях величина
- [math]\displaystyle{ \frac {v^2}{2} + gh + \mathcal P = \text{const} }[/math]
постоянна вдоль любой линии тока и любой вихревой линии. Соотношение справедливо для течения в любом потенциальном поле, при этом [math]\displaystyle{ gh }[/math] заменяется на потенциал массовой силы [math]\displaystyle{ \varphi }[/math].
Уравнение Громеки — Лэмба[23][24] (квадратные скобки обозначают векторное произведение) имеет вид:
- [math]\displaystyle{ \frac{\partial \vec v}{\partial t}+\operatorname{grad}\left(\frac{v^2}{2}\right)+\left[\mathrm{rot}\,\vec v , \vec v\right]=-\frac1\rho\operatorname{grad}p+\vec{F} }[/math]
В силу сделанных предположений [math]\displaystyle{ \frac{\partial \vec v}{\partial t}=0, }[/math] [math]\displaystyle{ \frac{\operatorname{grad}p}{\rho}=\operatorname{grad}{\cal P} }[/math] и [math]\displaystyle{ \vec{F}=-\operatorname{grad}\varphi }[/math] (в частном случае однородной силы тяжести её потенциал равен [math]\displaystyle{ \varphi=g\,h }[/math]), так что уравнение Громеки — Лэмба принимает вид:
- [math]\displaystyle{ \operatorname{grad}\left(\frac{v^2}{2}+\varphi+{\cal P}\right)+\left[\mathrm{rot}\,\vec v , \vec v\right]=0 }[/math]
Скалярное произведение этого уравнения на единичный вектор [math]\displaystyle{ \vec{l}=\frac{\vec{v}}{v}, }[/math] касательный к линии тока, даёт:
- [math]\displaystyle{ \frac\partial{\partial l}\left(\frac{v^2}{2}+\varphi+{\cal P}\right)=0 }[/math]
так как произведение градиента на единичный вектор даёт производную по направлению [math]\displaystyle{ \frac\partial{\partial l} }[/math], а векторное произведение перпендикулярно направлению скорости. Следовательно, вдоль линии тока [math]\displaystyle{ \frac{v^2}{2}+\varphi+{\cal P}=\mathrm{const}. }[/math] Такое соотношение справедливо и для вихревой линии, касательный вектор к которой в каждой точке направлен по [math]\displaystyle{ \mathrm{rot}\,\vec v. }[/math]
Для безвихревых баротропных течений, скорость которых может быть выражена в виде градиента потенциала скорости [math]\displaystyle{ \vec v=\operatorname{grad}\psi }[/math], интеграл Бернулли в виде [math]\displaystyle{ \frac{\partial\psi}{\partial t}+\frac {\left(\operatorname{grad}\psi\right)^2}{2}+ gh+ {\cal P} =\mathrm{const} }[/math][K 4] сохраняется также в нестационарных течениях, причём постоянная в правой части имеет одинаковое значение для всего течения[25].
Формула Сен-Венана — Ванцеля
Если в течении совершенного газа выполняется адиабатический закон[26]
- [math]\displaystyle{ p=\frac{p_0}{\rho_0^\gamma}\rho^\gamma,\qquad\rho=\frac{\rho_0}{p_0^{1/\gamma}}p^{1/\gamma},\qquad{\cal P}=-\frac{\gamma}{\gamma-1}\frac{p_0}{\rho_0}\left[1-\left(\frac{p}{p_0}\right)^{(\gamma-1)/\gamma}\right], }[/math]
то уравнение Бернулли выражается так[27] (вкладом от силы тяжести обычно можно пренебречь):
- [math]\displaystyle{ \frac{v^2}{2}-\frac{\gamma}{\gamma-1}\frac{p_0}{\rho_0}\left[1-\left(\frac{p}{p_0}\right)^{(\gamma-1)/\gamma}\right]=\mathrm{const} }[/math] вдоль линии тока или вихревой линии. Здесь
- [math]\displaystyle{ \gamma = \frac{C_p}{C_V} }[/math] — показатель адиабаты газа, выражающийся через теплоёмкости при постоянном давлении и при постоянном объёме,
- [math]\displaystyle{ p,\ \rho }[/math] — давление и плотность газа,
- [math]\displaystyle{ p_0,\ \rho_0 }[/math] — условно выбранные постоянные (одинаковые для всего течения) значения давления и плотности.
С помощью полученной формулы находят скорость газа, вытекающего из сосуда с высоким давлением через малое отверстие. Удобно давление и плотность газа в сосуде, скорость газа в котором равна нулю, принять за [math]\displaystyle{ p_0,\ \rho_0, }[/math] тогда скорость истечения выражается через внешнее давление [math]\displaystyle{ p }[/math] по формуле Сен-Венана — Ванцеля[28]:
- [math]\displaystyle{ v^2=\frac{2\gamma}{\gamma-1}\frac{p_0}{\rho_0}\left[1-\left(\frac{p}{p_0}\right)^{(\gamma-1)/\gamma}\right]. }[/math]
Термодинамика закона Бернулли
Из термодинамики следует, что вдоль линии тока любого стационарного течения идеальной жидкости
- [math]\displaystyle{ \frac{v^2}{2} + w + \varphi = \text{const},\quad s = \text{const}, }[/math]
где [math]\displaystyle{ w }[/math] — энтальпия единицы массы, [math]\displaystyle{ \varphi }[/math] — гравитационный потенциал (равный [math]\displaystyle{ gz }[/math] для однородной силы тяжести), [math]\displaystyle{ s }[/math] — энтропия единицы массы.
1. Уравнение Эйлера для стационарного ([math]\displaystyle{ \partial \vec v/\partial t = 0 }[/math]) движения идеальной жидкости в поле силы тяжести[29] имеет вид
- [math]\displaystyle{ (\vec v\cdot\nabla) \vec v = -\frac1{\rho} \nabla p +\vec g, }[/math]
где ускорение силы тяжести можно выразить через гравитационный потенциал [math]\displaystyle{ \vec g=-\nabla\varphi }[/math] (для однородного поля [math]\displaystyle{ \varphi = gh }[/math]), точка между векторами в круглых скобках означает их скалярное произведение.
2. Скалярное произведение этого уравнения на единичный вектор [math]\displaystyle{ \vec{l}=\frac{\vec{v}}{v}, }[/math] касательный к линии тока даёт
- [math]\displaystyle{ \frac\partial{\partial l}\left(\frac{v^2}{2}+\varphi\right)=-\frac1\rho\frac{\partial p}{\partial l}, }[/math]
так как произведение градиента на единичный вектор даёт производную по направлению [math]\displaystyle{ \frac\partial{\partial l}. }[/math]
3. Термодинамическое дифференциальное соотношение
- [math]\displaystyle{ \mathrm{d}w = \frac1\rho \mathrm{d}p + T \mathrm{d}s, }[/math]
где [math]\displaystyle{ w }[/math] — энтальпии единицы массы, [math]\displaystyle{ T }[/math] — температура и [math]\displaystyle{ s }[/math] — энтропия единицы массы, даёт
- [math]\displaystyle{ \frac{\partial w}{\partial l}= \frac{1}{\rho}\frac{\partial p}{\partial l}+T\frac{\partial s}{\partial l},\quad }[/math] так что [math]\displaystyle{ \frac{\partial}{\partial l} \left( \frac{v^2}{2} + w + \varphi \right) = T\frac{\partial s}{\partial l}. }[/math]
В стационарном течении идеальной жидкости все частицы, движущиеся вдоль данной линии тока, имеют одинаковую энтропию[30] ([math]\displaystyle{ \partial s/\partial l = 0 }[/math]), поэтому вдоль линии тока:
- [math]\displaystyle{ s = \text{const},\quad \frac{v^2}{2} + w + \varphi = \text{const}. }[/math]
Интеграл Бернулли применяют в инженерных расчётах, в том числе для сред, весьма далёких по своим свойствам от идеального газа, например для водяного пара, используемого в качестве теплоносителя в паровых турбинах. При этом могут использоваться так называемые диаграммы Молье, представляющие удельную энтальпию (по оси ординат) как функцию удельной энтропии (по оси абсцисс), и, например, давления (или температуры) в виде семейства изобар (изотерм). В этом случае последовательность состояний вдоль линии тока лежит на некоторой вертикальной линии ([math]\displaystyle{ s = \text{const} }[/math]). Длина отрезка этой линии, отсекаемого двумя изобарами, соответствующими начальному и конечному давлению теплоносителя, равна половине изменения квадрата скорости[31].
Обобщения интеграла Бернулли
Интеграл Бернулли также сохраняется при переходе потока через фронт ударной волны, в системе отсчета, в которой ударная волна покоится[32]. Однако при таком переходе энтропия среды не остаётся постоянной (возрастает), поэтому соотношение Бернулли является лишь одним из трёх соотношений Гюгонио, наряду с законами сохранения массы и импульса, связывающих состояние среды за фронтом с состоянием среды перед фронтом и со скоростью ударной волны.
Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений[33]), в магнитной гидродинамике[34], феррогидродинамике[35]. В релятивистской гидродинамике, когда скорости течения становятся сравнимыми со скоростью света [math]\displaystyle{ c }[/math], интеграл формулируется в терминах релятивистски инвариантных[36] удельной энтальпии и удельной энтропии[37].
Комментарии
- ↑ В записи Д.Бернулли в явном виде не фигурировало внутреннее давление в жидкости[8][9][10].
- ↑ «…[Вывод теоремы Бернулли из уравнения энергии] обедняет содержание теоремы Бернулли … Интеграл Бернулли, вообще говоря, не зависит от уравнения энергии, хотя действительно совпадает с ним для изоэнтропического и адиабатического движения совершенного газа»[20].
- ↑ «Два … пути получения уравнения Бернулли не эквивалентны. При энергетическом выводе нет необходимости в предположении об изэнтропичности течения. При интегрировании уравнения движения интегралы Бернулли получаются не только вдоль линий тока, но и вдоль вихревых линий»[21].
- ↑ В русскоязычной литературе интеграл Бернулли для потенциальных течений несжимаемой или баротропной жидкости известен как интеграл Коши — Лагранжа[25]
Примечания
- ↑ 1,0 1,1 Ландсберг Г. С. Закон Бернулли, 1985.
- ↑ 2,0 2,1 2,2 2,3 Вишневецкий С. Л. Бернулли уравнение, 1988.
- ↑ Титьенс О., Прандтль Л. Гидро- и аэромеханика, 1933.
- ↑ 4,0 4,1 4,2 4,3 4,4 Лойцянский Л. Г. Механика жидкости и газа, 2003, §24. Теорема Бернулли.
- ↑ Милн-Томсон Л. М. Теоретическая гидродинамика, 1964.
- ↑ Седов Л. И. Механика сплошной среды, 1970.
- ↑ Чёрный Г. Г. Газовая динамика, 1988.
- ↑ Трусделл К. Очерки по истории механики, 2002.
- ↑ Михайлов Г. К., 1999, с. 17.
- ↑ Darrigol O. A history of hydrodynamics, 2005, с. 9.
- ↑ Трусделл К. Очерки по истории механики, 2002, с. 255, 257.
- ↑ Euler L. Continuation des recherches, 1755 (1757), с. 331.
- ↑ 13,0 13,1 Сивухин Д. В. Механика, 1989, §94. Стационарное движение идеальной жидкости. Уравнение Бернулли.
- ↑ Чугаев Р. Р. Гидравлика. — Л.: Энергия, 1975. — 600 с.
- ↑ Сивухин Д. В. Механика, 1989, §95. Примеры на применение уравнения Бернулли. Формула Торричелли.
- ↑ Сивухин Д. В. Механика, 1989, §94, формула (94.6).
- ↑ Молоканов Ю. К. Процессы и аппараты нефтегазопереработки. — М.: Химия, 1980. — С. 60. — 408 с.
- ↑ Я. И. Перельман. Отчего притягиваются корабли?. Дата обращения: 27 декабря 2018. Архивировано 11 мая 2012 года.
- ↑ 19,0 19,1 19,2 19,3 19,4 Напор, 1992.
- ↑ Бэтчелор Дж. Введение в динамику жидкости, 1973, Примечание Г. Ю. Степанова, с. 208.
- ↑ Гольдштейн Р. В., Городцов В. А. Механика сплошных сред, 2000, с. 104.
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (9).
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (7).
- ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VIII. §2, уравнение (2.1).
- ↑ 25,0 25,1 Лойцянский Л. Г. Механика жидкости и газа, 2003, §42. Интеграл Лагранжа — Коши.
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (29).
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (30).
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (31).
- ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (2.4).
- ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VII. §2. Функция давления.
- ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 446.
- ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, §85.
- ↑ Голубкин В. Н., Сизых Г. Б. О некоторых общих свойствах плоскопараллельных течений вязкой жидкости // Известия АН СССР, серия Механика жидкости и газа : журнал. — 1987. — № 3. — С. 176–178. — doi:10.1007/BF01051932.
- ↑ Куликовский А. Г., Любимов Г. А. Магнитная гидродинамика. — М.: Физматлит, 1962. — С. 54. — 248 с.
- ↑ Розенцвейг Р. Феррогидродинамика / Пер. с англ. под ред. В. В. Гогосова. — М.: Мир, 1989. — С. 136. — 359 с. — ISBN 5-03-000997-3.
- ↑ Зубарев Д. Н., Релятивистская термодинамика, 1994.
- ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (134.11).
Литература
- Бэтчелор Дж. Введение в динамику жидкости / Пер. с англ. под ред. Г. Ю. Степанова. — М.: Мир, 1973. — 760 с.
- Вишневецкий С. Л. Бернулли уравнение // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова-Бома эффект — Длинные линии. — С. 187. — 704 с.
- Гольдштейн Р. В., Городцов В. А. Механика сплошных сред. Часть 1. — М.: Физматлит, 2000. — 256 с. — ISBN 5-02-015555-1.
- Зубарев, Д. Н. Релятивистская термодинамика // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 333—334. — 704 с. — ISBN 5-85270-087-8.
- Ландау Л. Д., Лифшиц Е. М. Гидродинамика. — Издание 5-е, стереотипное. — М.: Физматлит, 2001. — 736 с. — («Теоретическая физика», том VI). — ISBN 5-9221-0121-8.
- Лойцянский Л. Г. Механика жидкости и газа. — М.: Дрофа, 2003. — 842 с. — ISBN 5-7107-6327-6.
- Милн-Томсон Л. М. Теоретическая гидродинамика. — М.: Мир, 1964. — 656 с.
- Михайлов Г. К. Становление гидравлики и гидродинамики в трудах петербургских академиков (XVIII) // Известия Академии наук, серия Механика жидкости и газа : журнал. — 1999. — Вып. 6. — С. 7–25.
- Напор // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный компрессор — Пойнтинга теорема. — С. 242. — 672 с. — ISBN 5-85270-019-3.
- Поль Р. В. Механика, акустика и учение о теплоте. — Рипол Классик, 2013. — 490 с. — ISBN 5458431251, 9785458431255.
- Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — 568 с.
- Сивухин Д. В. Общий курс физики. — Издание 3-е, исправленное и дополненное. — М.: Наука, 1989. — Т. I. Механика. — 576 с. — ISBN 5-02-014054-6.
- Титьенс О., Прандтль Л. Гидро- и аэромеханика. — М.-Л.: ГТТИ, 1933. — Т. 1. — 224 с.
- Трусделл К. Очерки по истории механики. — М. — Ижевск: Институт компьютерных исследований, 2002. — 316 с. — ISBN 5-93972-192-3.
- Фабер Т. Е. Гидроаэродинамика / Пер. с англ. под ред. А. А. Павельева. — М.: Постмаркет, 2001. — 560 с. — ISBN 5-901095-04-9.
- Чёрный Г. Г. Газовая динамика. — М.: Наука, 1988. — 424 с. — ISBN 5-02-013814-2.
- §182. Закон Бернулли // Элементарный учебник физики / Под ред. Г. С. Ландсберга. — М.: Наука, 1985. — Т. 1. Механика. Теплота. Молекулярная физика.
- Darrigol O. Worlds of flow. A history of hydrodynamics from the Bernoullis to Prandtl. — Oxford: Oxford University Press, 2005. — 356 с. — ISBN 978-0-19-856843-8.
- Euler L. Continuation des recherches sur la théorie du mouvement des fluides // Mémoires de l'Académie royale des sciences et belles lettres. — Berlin, 1755 (1757). — Т. 11. — С. 316—361.
- Truesdell, Clifford Ambrose. Rational fluid mechanics, 1687–1765. Editor’s introduction to Euleri Opera omnia II 12 // Leonardi Euleri. Opera Omnia. — Lausanne: Auctoritate et Impensis, Societas Scientiarum Naturalium Helveticae, 1954. — Т. 12. — С. I—CXXV. — (II).
Ссылки