Форма волны
Фо́рма волны́ — наглядное представление формы сигнала, такого как волна, распространяющегося в физической среде, или его абстрактное представление[1][2].
Во многих случаях среда, в которой распространяется волна, не позволяет наблюдать её форму визуально. В этом случае, термин «волна» относится к форме графика величины, изменяющейся по времени или зависящей от расстояния. Для наблюдения формы электрических колебаний может использоваться осциллограф, отображающий на экране значение измеряемой величины и его изменение во времени.
В более широком смысле термины «сигнал», «волна», «колебание» используется для формы графика значений любой величины, изменяющейся по времени или пространстве.
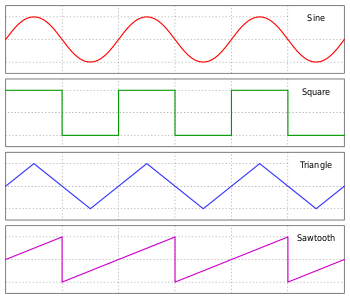
Примеры волн (колебаний) основных форм
Наиболее часто рассматриваются периодические сигналы следующего вида ([math]\displaystyle{ t }[/math] — время, [math]\displaystyle{ A }[/math] — амплитуда колебания [math]\displaystyle{ T }[/math] — период, [math]\displaystyle{ f = 1/T }[/math] — частота основной гармоники).
Синусоидальное колебание
Стандарт ГОСТ Р ИСО/МЭК 19762-4-2011 отределяет синусоидальное колебание как базовую форму волны, характеризующейся единственной частотой и длиной волны и используемой для передачи данных или информации с помощью модуляции некоторого параметра волны[3].
Амплитуда синусоидальной волны изменяется в соответствии с тригонометрической функцией синуса:
- [math]\displaystyle{ x(t) = A \sin (\omega t + \varphi_0), }[/math]
- где [math]\displaystyle{ \omega }[/math] — циклическая частота, показывающая, на сколько радиан изменяется фаза колебания за 1 с (радиан/с),
- [math]\displaystyle{ \omega = 2 \pi f }[/math],
- [math]\displaystyle{ \varphi_0 }[/math] — начальная фаза колебаний, которая определяет значение полной фазы колебания в момент времени [math]\displaystyle{ t = 0. }[/math]
Спектр синусоидальной волны содержит только одну спектральную линию с частотой колебания.
Прямоугольное периодическое колебание
Сигналы такого рода, как правило, используется для представления и передачи цифровых данных. Аналитически может быть записан многими способами, например, через функцию Хевисайда [math]\displaystyle{ h(t) }[/math]:
- [math]\displaystyle{ x(t) = 2\ A \sum_{n=-\infty}^\infty \left[h \left(\frac{t}{T} - n\right) - h \left(\frac{t}{T} - n - \frac{1}{S} \right) \right] - 1, }[/math]
- где [math]\displaystyle{ S }[/math] — скважность.
При [math]\displaystyle{ S = 2 }[/math] описывает меандр — периодическое колебание у которого длительности положительной и отрицательной полуволн равны.
Спектр прямоугольной волны линейчатый, причём у меандра в спектре отсутствуют чётные гармоники, амплитуда гармоник падает при увеличении частоты на 6 дБ/октава:
- [math]\displaystyle{ x(t) = \frac {4} {\pi} \sum_{k = 1}^\infty \frac{\sin\left[2\pi(2k - 1)ft\right]}{2k - 1} = \frac{4}{\pi} \left[\sin(2\pi ft) + \frac{1}{3} \sin(6\pi ft) + \frac {1} {5} \sin(10 \pi ft) + \dots \right]. }[/math]
Треугольная симметричная волна
Половину периода линейно нарастает, вторую половину периода падает с той же скоростью. Аналитически может быть записана в виде:
- [math]\displaystyle{ x(t) = \frac{2A}{\pi}\arcsin\left[\sin\left(\frac{2\pi}{T}t\right)\right]. }[/math]
Спектр треугольной волны линейчатый, в спектре отсутствуют чётные гармоники, амплитуда гармоник падает при увеличении частоты на 12 дБ/октава:
- [math]\displaystyle{ x(t) = \frac {8} {\pi^2}\sum_{k=0}^{\infty} \frac {(-1)^k} {(2k+1)^2} \sin\left[\frac {2\pi (2k+1)}{T}t\right]. }[/math]
Пилообразная волна
Линейно нарастает весь период, в конце периода мгновенно падает до начального значения. Графически выглядит как зубья пилы. В технике пилообразное напряжение или пилообразный ток используется в развёртках осциллографов и для сканирования телевизионного растра. Аналитически может быть описана выражением:
- [math]\displaystyle{ x(t) = \frac{2A}{\pi} \operatorname{arcctg} \left( \operatorname{tg} \frac {\pi t}{T} \right). }[/math]
Спектр пилообразной волны линейчатый, в спектре присутствуют как чётные, так и нечётные гармоники, амплитуда гармоник падает при увеличении частоты на 6 дБ/октава:
- [math]\displaystyle{ x(t) = \frac{A}{\pi}\sum_{k=1}^{\infty} {(-1)}^{k} \frac{\sin(2\pi kft)}{k}. }[/math]
Другие формы волн
Другие формы сигналов часто называют составными или сложными, так как они могут быть описаны в виде суммы нескольких синусоидальных волн или суммой других функций.
В частности, любое периодическое колебание представимо в виде ряда Фурье или интеграла Фурье в случае непериодического колебания.
Примечания
- ↑ Waveform Definition. techterms.com. Дата обращения: 9 декабря 2015. Архивировано 20 декабря 2019 года.
- ↑ David Crecraft, David Gorham, Electronics, 2nd ed., ISBN 0748770364, CRC Press, 2002, p. 62
- ↑ ГОСТ Р ИСО/МЭК 19762-4-2011 Информационные технологии (ИТ). Технологии автоматической идентификации и сбора данных (АИСД). Гармонизированный словарь. Часть 4. Общие термины в области радиосвязи.. Дата обращения: 25 сентября 2020. Архивировано 18 февраля 2020 года.
Литература
- Yuchuan Wei, Qishan Zhang. Common Waveform Analysis: A New And Practical Generalization of Fourier Analysis. Springer US, Aug 31, 2000
- Hao He, Jian Li, and Petre Stoica. Waveform design for active sensing systems: a computational approach. Cambridge University Press, 2012.
- Solomon W. Golomb, and Guang Gong. Signal design for good correlation: for wireless communication, cryptography, and radar. Cambridge University Press, 2005.
- Jayant, Nuggehally S and Noll, Peter. Digital coding of waveforms: principles and applications to speech and video. Englewood Cliffs, NJ, 1984.
- Soltanalian M. Signal Design for Active Sensing and Communications. Uppsala Dissertations from the Faculty of Science and Technology (printed by Elanders Sverige AB), 2014.
- Nadav Levanon, and Eli Mozeson. Radar signals. Wiley. com, 2004.
- Jian Li, and Petre Stoica, eds. Robust adaptive beamforming. New Jersey: John Wiley, 2006.
- Fulvio Gini, Antonio De Maio, and Lee Patton, eds. Waveform design and diversity for advanced radar systems. Institution of engineering and technology, 2012.
- John J. Benedetto, Ioannis Konstantinidis, and Muralidhar Rangaswamy. «Phase-coded waveforms and their design.» IEEE Signal Processing Magazine, 26.1 (2009): 22-31.
Ссылки
- Erfassung von Wellenformen beim Oszilloskop (abgerufen am 27. Juli 2018)
- Wellenformen nach Maß (abgerufen am 27. Juli 2018)
- Radar-Wellenformen erzeugen, messen und auswerten (abgerufen am 27. Juli 2018)
- Wellenform basierte Quellenlokalisierung im Vergleich zu konventionellen Methoden (abgerufen am 27. Juli 2018)