Собственное равновесие

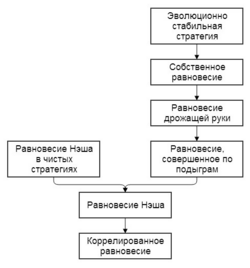
Шаблон:Концепция решения Собственное равновесие — принцип оптимальности в некооперативных играх, представляющий собой сужение равновесия дрожащей руки. Введён Р. Б. Майерсоном.

В отличие от равновесия дрожащей руки, данный принцип основан на предположении, что более затратные отклонения от равновесных стратегий возникают со значительно меньшей вероятностью, нежели менее затратные.

Определение

Для заданной игры в нормальной форме [math]\displaystyle{ \Gamma = \lt I, \{X_i\}_{i \in I}, \{H_i\}_{i \in I}\gt }[/math] и параметра ε > 0, профиль вполне смешанных стратегий называется ε-собственным, если выполнено следующее условие: для двух чистых стратегий игрока i, x', x'' ∈ X_i, таких, что его ожидаемый выигрыш при использовании стратегии x' меньше, нежели при использовании x'', вероятность использования x' не превышает εp, где p — вероятность использования чистой стратегии x''.

Профиль стратегий в игре называется собственным равновесием, если он является пределом при ε→0 последовательности ε-собственных вполне смешанных профилей стратегий.

Пример

Рассмотрим вариант игры «орел-решка», приведенный в таблице.

	Орел	Решка	Забрать монету
Орел	-1, 1	0, 0	-1, 1
Решка	0, 0	-1, 1	-1, 1

Игрок 1, выбирающий строку, прячет монету одной из сторон вверх. Если Игрок 2, выбирающий столбец, угадывает сторону, он получает эту монету. Однако, в этом варианте игры он имеет еще одну стратегию, забрать монету, не угадывая. Равновесиями Нэша в данной игре являются ситуации, в которых Игрок 2 использует стратегию «забрать монету» с вероятностью 1, а Игрок 1 — любую смешанную стратегию. Более того, любая такая ситуация является также и равновесием дрожащей руки. Интуитивно это означает, что Игроку 1, в условиях, когда Игрок 2 в любом случае забирает монету, нет необходимости оптимизировать свою стратегию.

В то же время, единственным собственным равновесием в этой игре является использование Игроком 1 своих стратегий «орел» и «решка» с вероятностями 1/2, а Игроком 2 — стратегии «забрать монету» с вероятностью 1. Наличие этого равновесия связано с тем, что Игрок 1 по-прежнему учитывает возможность невероятного события, когда Игрок 2 не забирает монету, а пытается угадать. При этом указанная стратегия Игрока 1 будет минимизировать его ожидаемый проигрыш.

Соотношение равновесных концепций решения. Стрелками обозначено направление от рафинирований к менее требовательным концепциям

Литература

• Myerson, R.B. Refinements of the Nash equilibrium concept // International Journal of Game Theory. — 1978. — Vol.15. — P. 133—154.

• van Damme, E. A relationship between perfect equilibria in extensive form games and proper equilibria in normal form games // International Journal of Game Theory — 1984. — Vol.13. — P.1-13.