Предел (математика)

Преде́л — одно из основных понятий математического анализа, на него опираются такие фундаментальные разделы анализа, как непрерывность, производная, интеграл, бесконечные ряды и др. Различают предел последовательности и предел функции^[1].

Понятие предела на интуитивном уровне использовалось ещё во второй половине XVII века Ньютоном, а также математиками XVIII века, такими как Эйлер и Лагранж. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.

История

Обоснование термина

Операция взятия предела в математическом анализе называется предельным переходом^[2]. Интуитивное понятие о предельном переходе использовалось ещё учеными Древней Греции при вычислении площадей и объёмов различных геометрических фигур. Методы решения таких задач в основном были развиты Архимедом.

При создании дифференциального и интегрального исчислений математики XVII века (и, прежде всего, Ньютон) также явно или неявно использовали понятие предельного перехода. Впервые определение понятия предела было введено в работе Валлиса «Арифметика бесконечных величин» (XVII век), однако исторически это понятие не лежало в основе дифференциального и интегрального исчислений.

Лишь в XIX веке в работах Коши теория пределов была использована для строгого обоснования математического анализа. Дальнейшей разработкой теории пределов занимались Вейерштрасс и Больцано.

С помощью теории пределов в первой половине XIX века было, в частности, обосновано использование в анализе бесконечных рядов, которые явились удобным аппаратом для построения новых функций^[3].

Символ предела

Общепринятый символ предела [math]\displaystyle{ \lim_{x \to a} f(x) }[/math] был предложен Симоном Люилье (1787 год) в следующем формате: [math]\displaystyle{ \operatorname{lim.}x:a; }[/math] это обозначение получило поддержку Коши (1821). Точка после lim вскоре исчезла^[4]. Близкое к современному обозначение предела ввёл Вейерштрасс, хотя вместо привычной нам стрелки он использовал знак равенства: [math]\displaystyle{ \operatorname{Lim} _{x=a} }[/math]^[5]. Стрелка появилась в начале XX века сразу у нескольких математиков^[6].

Обозначения для одностороннего предела вида [math]\displaystyle{ \lim_{x \to a+0} f(x) }[/math] первым предложил Дирихле (1837) в виде: [math]\displaystyle{ f(a+0), f(a-0). }[/math] Мориц Паш (1887) ввёл другие важные понятия — верхнего и нижнего предела, которые записывал в виде: [math]\displaystyle{ \lim \sup }[/math] и [math]\displaystyle{ \lim \inf }[/math] соответственно. За рубежом эта символика стала стандартной, а в отечественной литературе преобладают другие обозначения: [math]\displaystyle{ \varlimsup_{n \to \infty} x_n,\ \varliminf_{n \to \infty} x_n, }[/math] введенные Альфредом Прингсхаймом в 1898 году^[7].

Предел последовательности

Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом порядкового номера.

Число [math]\displaystyle{ a }[/math] называется пределом последовательности [math]\displaystyle{ x_1,x_2,...,x_n,... }[/math], если

[math]\displaystyle{ \forall\text{ } \varepsilon \gt 0 \text{, } \exists \text{ } N(\varepsilon)\text{, }\forall \text{ } n\gt N(\varepsilon) \text{ }\text{ }|x_n-a|\lt \varepsilon }[/math].

Предел последовательности обозначается [math]\displaystyle{ \lim_{n\to +\infty} x_n }[/math]. Допускается обозначение [math]\displaystyle{ \lim x_n }[/math].^{[источник не указан 1435 дней]}

Свойства:

Если предел последовательности существует, то он единственный.
[math]\displaystyle{ \lim c = c }[/math][math]\displaystyle{ ,\,c={\rm const}. }[/math]
[math]\displaystyle{ \lim (x_n + y_n) = \lim x_n + \lim y_n }[/math] (если оба предела существуют)
[math]\displaystyle{ \lim (q x_n) = q \lim x_n }[/math] [math]\displaystyle{ ,\,q={\rm const}. }[/math]
[math]\displaystyle{ \lim (x_n y_n) = \lim x_n \lim y_n }[/math] (если оба предела существуют)
[math]\displaystyle{ \lim (x_n / y_n) = \lim x_n / \lim y_n }[/math] (если оба предела существуют и знаменатель правой части не ноль)
Если [math]\displaystyle{ a_n \gt x_n \gt b_n \forall n }[/math] и [math]\displaystyle{ \lim a_n = \lim b_n }[/math] , то [math]\displaystyle{ \lim x_n = \lim a_n = \lim b_n }[/math] (теорема «о зажатой последовательности», также известная, как «теорема о двух милиционерах»)

Предел функции

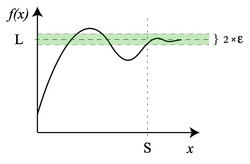
График функции, предел которой при аргументе, стремящемся к бесконечности, равен [math]\displaystyle{ L }[/math].

Функция [math]\displaystyle{ f(x) }[/math] имеет предел [math]\displaystyle{ A }[/math] в точке [math]\displaystyle{ x_0 }[/math], если для всех значений [math]\displaystyle{ x }[/math], достаточно близких к [math]\displaystyle{ x_0 }[/math], значение [math]\displaystyle{ f(x) }[/math] близко к [math]\displaystyle{ A }[/math].

Число b называется пределом функции [math]\displaystyle{ f(x) }[/math] в точке [math]\displaystyle{ a }[/math], если [math]\displaystyle{ \forall \varepsilon \gt 0 }[/math] существует [math]\displaystyle{ \delta \gt 0 }[/math], такое что [math]\displaystyle{ \forall x, 0 \lt |x-a| \lt \delta }[/math] выполняется [math]\displaystyle{ |f(x) - b| \lt \varepsilon }[/math].

Для пределов функций справедливы свойства, аналогичные пределам последовательностей, например, [math]\displaystyle{ \lim_{x\to x_0} (f(x)+ g(x))= \lim_{x\to x_0} f(x)+ \lim_{x\to x_0} g(x) }[/math] — предел суммы равен сумме пределов, если все пределы существуют.

Понятие предела последовательности на языке окрестностей

Пусть [math]\displaystyle{ X }[/math] — некоторое множество, на котором определено понятие окрестности [math]\displaystyle{ U }[/math] (например, метрическое пространство). Пусть [math]\displaystyle{ x_i \in X }[/math] — последовательность точек (элементов) этого множества. Говорят, что [math]\displaystyle{ x \in X }[/math] есть предел этой последовательности, если в любой окрестности точки [math]\displaystyle{ x }[/math] лежат почти все члены последовательности, или [math]\displaystyle{ \forall \text{ }U(x) \text{ } \exist\text{ } n,\text{ } \forall\text{ } i\gt n \text{ }\text{ } x_i \in U(x) }[/math]

Замечательные пределы

Замечательные пределы — термины, использующиеся в советских и российских учебниках по математическому анализу для обозначения двух широко известных математических тождеств со взятием предела:

Первый замечательный предел:
[math]\displaystyle{ \lim_{x \to 0}\frac{\sin x}{x} = 1. }[/math]
Второй замечательный предел:
[math]\displaystyle{ \lim_{x \to \infty}\left(1 + \frac{1}{x}\right)^x = e. }[/math]

Замечательные пределы и их следствия используются при раскрытии неопределённостей для нахождения других пределов.

Ультрапредел

Ультрапредел — это конструкция, позволяющая определить предел для широкого класса математических объектов. В частности, она работает для числовых последовательностей и последовательностей точек в метрическом пространстве, допускает обобщения на последовательности метрических пространств и последовательности функций на них. Эта конструкция часто используется, чтобы избежать многократного перехода к подпоследовательности. Эта конструкция использует существование неглавного ультрафильтра, доказательство которого в свою очередь использует аксиому выбора.

См. также

Примечания

↑ Математическая энциклопедия, 1984, с. 556.
↑ Хинчин А. Я. Восемь лекций по математическому анализу. — М.— Л., Гостехиздат, 1948. — С. 14
↑ Цыпкин А. Г. Справочник по математике. — М.: «Наука», 1983.
↑ Хайрер Э., Ваннер Г. Математический анализ в свете его истории. — М.: Научный мир, 2008. — 396 с. — ISBN 978-5-89176-485-9. — С. 172.
↑ Юшкевич А. П. Развитие понятия предела до К. Вейерштрасса // Историко-математические исследования. — М.: Наука, 1986. — № 30. — С. 76.
↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — С. 133—135. — 248 с. — ISBN 978-5-382-00839-4.
↑ Cajori F. A History of Mathematical Notations. Vol. 1 (1929 reprint), §631—637. — NY: Cosimo, Inc., 2007. — xvi + 456 p. — ISBN 978-1-60206-684-7.

Литература

Предел // Математическая энциклопедия (в 5 томах). — М.: Советская энциклопедия, 1984. — Т. 4.

[_06f5d90dda1bed7c-1] Математическая энциклопедия, 1984, с. 556.

[2] Хинчин А. Я. Восемь лекций по математическому анализу. — М.— Л., Гостехиздат, 1948. — С. 14

[3] Цыпкин А. Г. Справочник по математике. — М.: «Наука», 1983.

[LIMES-4] Хайрер Э., Ваннер Г. Математический анализ в свете его истории. — М.: Научный мир, 2008. — 396 с. — ISBN 978-5-89176-485-9. — С. 172.

[5] Юшкевич А. П. Развитие понятия предела до К. Вейерштрасса // Историко-математические исследования. — М.: Наука, 1986. — № 30. — С. 76.

[6] Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — С. 133—135. — 248 с. — ISBN 978-5-382-00839-4.

[7] Cajori F. A History of Mathematical Notations. Vol. 1 (1929 reprint), §631—637. — NY: Cosimo, Inc., 2007. — xvi + 456 p. — ISBN 978-1-60206-684-7.

[1]

[2]

[3]

[4]

[5]

[6]

[7]