Линейное приближение

Линейное приближение (линейная аппроксимация) — приближение произвольной функции линейной функцией. Применяется для приближённых расчётов, в методе конечных разностей для решения дифференциальных уравнений.

График [math]\displaystyle{ f^*_a(x) }[/math] — касательная в точке [math]\displaystyle{ (a, f(a)) }[/math]

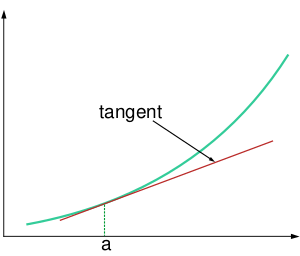
Для непрерывно дифференцируемой в окрестности точки [math]\displaystyle{ a }[/math] функции вещественной переменной [math]\displaystyle{ f(x) }[/math] линейное приближение определяется как:

[math]\displaystyle{ f^*_a(x) = f(a)+f'(a)(x-a) }[/math].

Определение получается из равенства из теоремы Тейлора [math]\displaystyle{ f(x) = f(a)+f'(a)(x-a)+R_2 }[/math] игнорированием остаточного члена [math]\displaystyle{ R_2(x) = o(|x-a|) }[/math]. Поскольку в ближайшей окрестности точки [math]\displaystyle{ a }[/math] значения этой функции близки к значениям [math]\displaystyle{ f(x) }[/math], её можно использовать как замену значений [math]\displaystyle{ f(x) }[/math] в приближённых вычислениях. При этом в общем случае погрешность возрастает при удалении от [math]\displaystyle{ a }[/math] и равна [math]\displaystyle{ R_2 }[/math]. График функции [math]\displaystyle{ f^*_a(x) }[/math] — касательная к графику [math]\displaystyle{ f(x) }[/math] в точке [math]\displaystyle{ a }[/math].

Определение естественным образом обобщается на многомерный случай (вместо производной используется матрица Якоби) и на случай банаховых пространств (с использованием производной Фреше).

Литература

• Weinstein, Alan; Marsden, Jerrold E. Calculus III (неопр.). — Berlin: Springer-Verlag, 1984. — С. 775. — ISBN 0-387-90985-0.
• Strang, Gilbert. Calculus (англ.). — Wellesley College, 1991. — P. 94. — ISBN 0-9614088-2-0.
• Bock, David; Hockett, Shirley O. How to Prepare for the AP Calculus (англ.). — Hauppauge, NY: Barrons Educational Series, 2005. — P. 118. — ISBN 0-7641-2382-3.