Золотой треугольник (геометрия)

Пентаграмма. Каждый угол является золотым треугольником. Фигура также содержит пять золотых гномонов, которые получаются соединением двух несмежных углов с центральным пятиугольником.

Золотые треугольники, вписанные в логарифмическую спираль

Золотой треугольник — это равнобедренный треугольник, в котором две боковые (равные) стороны находятся в золотой пропорции с основанием:

[math]\displaystyle{ { a \over b} = \varphi = {1 + \sqrt{5} \over 2}. }[/math]

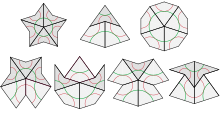
Золотые треугольники можно обнаружить в развёртках некоторых звёздчатых форм додекаэдра и икосаэдра.

Также, тот же треугольник обнаруживается в вершинах пентаграммы. Угол при вершине равен

[math]\displaystyle{ \theta = \cos^{-1}\left( {\varphi \over 2}\right) = {\pi \over 5} = 36^\circ. }[/math]

Из того, что сумма углов треугольника равна 180°, получаем, что углы при основании равны 72°. Золотой треугольник можно найти также в десятиугольнике, если соединить две смежные вершины с центром. Полученный треугольник будет золотым, поскольку: 180(10-2)/10=144° является внутренним углом десятиугольника, и деление его отрезком, соединяющим вершину с центром, даст половину, 144/2=72.

Золотой треугольник также замечателен уникальным соотношением углов 2:2:1.

Логарифмическая спираль

Последовательность золотых треугольников можно вписать в логарифмическую спираль. (Начиная с большого треугольника) делим угол при основании пополам, получаем следующую точку. Процесс деления может продолжаться бесконечно, создавая бесконечно много золотых треугольников. Логарифмическую спираль можно провести через полученные вершины. Эта спираль известна также как равноугольная спираль. Термин предложил Рене Декарт: «Если провести прямую из полюса к любой точке на кривой, она пересечёт кривую всегда под одним и тем же углом».

Золотой гномон

Золотой треугольник разбит на два треугольника Робинсона — золотой треугольник и золотой гномон.

Тесно связан с золотым треугольником золотой гномон, тупоугольный равнобедренный треугольник, в котором отношение длины равных (коротких) сторон к длине третьей стороны (основанию) является обратным к золотому отношению. Золотой гномон является уникальным треугольником с пропорцией углов 1:1:3. Его острые углы составляют 36°, то же значение, что и у угла при вершине золотого треугольника.

Расстояние AX и СX равны φ, что видно на рисунке. «Золотой треугольник имеет отношение основания к стороне, равное золотому отношению φ, в то время как золотой гномон имеет отношение боковой стороны к основанию, равное тому же золотому отношению» .

Плитки (сверху) и семь возможных типов вершин (снизу) в мозаике Пенроуза типа P2

Золотой треугольник может быть разрезан на золотой треугольник и золотой гномон. То же самое верно для золотого гномона. Золотой гномон и золотой треугольник с их равными сторонами (сторона гномона равна стороне треугольника) также являются тупым и острым треугольниками Робинсона.

Эти равнобедренные треугольники могут быть использованы для получения мозаик Пенроуза. Плитки Пенроуза состоят из «змеев» и «дротиков». «Змей» представляет собой дельтоид, состоящий из двух золотых треугольников, а «дротик» — дельтоид, состоящий из двух золотых гномонов.

См. также

• Золотое сечение
• Золотой прямоугольник
• Золотой ромб
• Треугольник Кеплера
• Лютня Пифагора
• Мозаика Пенроуза
• Пентаграмма

Литература

• Kimberly Elam. Geometry of Design. — New York: Princeton Architectural Press, 2001. — ISBN 1-56898-249-6.
• H.E. Huntley. The Divine Proportion: A Study In Mathematical Beauty. — New York: Dover Publications Inc, 1970. — ISBN 0-486-22254-3.
• Mario Livio. The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. — Broadway Books, 2002. — ISBN 0-7679-0815-5.
• Arthur Loeb. Concepts and Images: Visual Mathematics. — Boston: Birkhäuser Boston, 1992. — ISBN 0-8176-3620-X.

Ссылки

• Weisstein, Eric W. Golden triangle (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Golden gnomon (англ.) на сайте Wolfram MathWorld.
• Robinson triangles at Tilings Encyclopedia