Скин-эффект

Распределение плотности тока в цилиндрическом проводнике в поперечном сечении. Для переменного тока плотность тока экспоненциально убывает от поверхности вглубь проводника. Толщина скин-слоя [math]\displaystyle{ \delta }[/math] определяется как глубина от поверхности, на которой плотность тока уменьшается до [math]\displaystyle{ 1/e }[/math] (около 37 %) от значения на поверхности. Эта толщина зависит от частоты тока и электрических и магнитных свойств проводника.

Пове́рхностный эффе́кт, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.

Объяснение поверхностного эффекта

Физическая картина возникновения

Механизм возникновения скин-эффекта. Переменный ток в проводнике порождает переменное вихревое магнитное поле, силовые линии которого перпендикулярны к оси проводника За счёт электромагнитной индукции переменное магнитное поле порождает вихревое электрическое поле, вызывающее протекание вихревого тока Фуко, причём на поверхности проводника вихревой ток направлен по направлению тока проводника, а внутри проводника — противоположно. Это явление снижает ток в сердцевине проводника и увеличивает поверхностный ток.

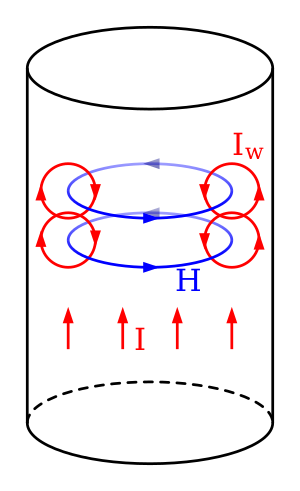
Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная [math]\displaystyle{ \frac{\partial \mathbf{B}}{\partial t} }[/math] направлена по касательной к линии индукции магнитного поля и, следовательно, линии [math]\displaystyle{ \frac{\partial \mathbf{B}}{\partial t} }[/math] также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции:

[math]\displaystyle{ \operatorname{rot} \, \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t} }[/math]

создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.

Уравнение, описывающее скин-эффект

Исходим из уравнения Максвелла:

[math]\displaystyle{ \operatorname{rot} \mathbf{B} = \mu \mathbf{j} }[/math]

и выражения для [math]\displaystyle{ \mathbf{j} }[/math] по закону Ома:

[math]\displaystyle{ \mathbf{j} = \gamma \mathbf{E}. }[/math]

Дифференцируя обе части полученного уравнения по времени, находим:

[math]\displaystyle{ \operatorname{rot} \frac{\partial \mathbf{B}}{\partial t} = \mu \gamma \frac{\partial \mathbf{E}}{\partial t}, }[/math]

[math]\displaystyle{ - \operatorname{rot} \operatorname{rot} \mathbf{E} = \mu \gamma \frac{\partial \mathbf{E}}{\partial t}, }[/math]

здесь [math]\displaystyle{ \gamma }[/math] — удельная проводимость материала проводника, [math]\displaystyle{ \gamma = 1/\rho,\ \ }[/math] [math]\displaystyle{ \rho }[/math] — удельное сопротивление материала проводника.

Поскольку [math]\displaystyle{ \operatorname{rot} \operatorname{rot} \mathbf{E} = \operatorname{grad} \operatorname{div} \mathbf{E} - \nabla^2 \mathbf{E} }[/math] и [math]\displaystyle{ \operatorname{div} \mathbf{E} = 0 }[/math] окончательно получаем:

[math]\displaystyle{ \nabla^2 \mathbf{E} = \mu \gamma \frac{\partial \mathbf{E}}{\partial t} }[/math].

здесь [math]\displaystyle{ \mu }[/math] — абсолютная магнитная проницаемость материала проводника, [math]\displaystyle{ \mu = \mu_0 \mu_m,\ \ }[/math] [math]\displaystyle{ \mu_0 }[/math] — магнитная проницаемость вакуума, [math]\displaystyle{ \mu_m }[/math] — относительная магнитная проницаемость материала проводника.

Скин-эффект в бесконечном проводнике с плоской границей.

Для упрощения решения предположим, что ток течёт вдоль оси [math]\displaystyle{ X }[/math] по однородному бесконечному проводнику, занимающему полупространство [math]\displaystyle{ y\gt 0 }[/math]. Поверхностью проводника является плоскость [math]\displaystyle{ Y=0. }[/math] Таким образом:

[math]\displaystyle{ j_x = j_x (y,t),\qquad j_y = j_z = 0, }[/math]

[math]\displaystyle{ E_x = E_x (y,t),\qquad E_y = E_z = 0. }[/math]

Тогда:

[math]\displaystyle{ \frac{\partial^2 E_x}{\partial y^2} = \mu \gamma \frac{\partial E_x}{\partial t}. }[/math]

В этом уравнении все величины гармонически зависят от [math]\displaystyle{ t, }[/math] и можно положить:

[math]\displaystyle{ E_x (y,t) = E_0 (y) e^{i \omega t}, }[/math]

здесь [math]\displaystyle{ \omega }[/math] - угловая частота.

Подставим это в наше уравнение и получим уравнение для [math]\displaystyle{ E_0 (y): }[/math]

[math]\displaystyle{ \frac{\partial^2 E_0}{\partial y^2} = i \gamma \mu \omega E_0. }[/math]

Общее решение этого уравнения:

[math]\displaystyle{ E_0 = A_1 e^{- k y} + A_2 e^{k y}. }[/math]

Учитывая, что [math]\displaystyle{ k = \sqrt{i \gamma \mu \omega} = \alpha (1 + i) }[/math], где [math]\displaystyle{ \alpha = \sqrt{ \frac{\gamma \mu \omega}{2} } }[/math], находим:

[math]\displaystyle{ E_0 = A_1 e^{- \alpha y}e^{-i \alpha y} + A_2 e^{\alpha y}e^{i \alpha y}. }[/math]

При удалении от поверхности проводника ([math]\displaystyle{ y \rightarrow \infty }[/math]) второе слагаемое неограниченно возрастает, что является физически недопустимой ситуацией. Следовательно, [math]\displaystyle{ A_2 = 0 }[/math], и в качестве физически приемлемого решения остаётся только первое слагаемое. Тогда решение задачи имеет вид:

[math]\displaystyle{ E_x = A_1 e^{- \alpha y} e^{i(\omega t - \alpha y)}. }[/math]

Взяв действительную часть от этого выражения и перейдя с помощью соотношения [math]\displaystyle{ \mathbf{j} = \gamma \mathbf{E} }[/math] к плотности тока, получим:

[math]\displaystyle{ j_x (y,t) =A_1 e^{- \alpha y} \cos{(\omega t - \alpha y)}. }[/math]

Принимая во внимание, что [math]\displaystyle{ j_x (0,0) = j_0 }[/math] — амплитуда плотности тока на поверхности проводника, приходим к следующему распределению объёмной плотности тока в проводнике:

[math]\displaystyle{ j_x (y,t) = j_0 e^{- \alpha y} \cos{(\omega t - \alpha y)}. }[/math]

Толщина скин-слоя

Зависимость глубины скин-слоя от частоты для различных материалов.
Материалы:
Mn-Zn – магнитомягкий марганцево-цинковый феррит марки 3C90 с начальной относительной магнитной проницаемостью 2300 (при 25 °C, 10 кГц) и удельным сопротивлением 5 Ом·м.
Al – алюминий, относительная проницаемость = 1, удельное сопротивление = 2,7⋅10^-8 Ом·м.
Cu – медь, относительная проницаемость = 1, удельное сопротивление = 1,7⋅10^-8 Ом·м.
Сталь 410 – ферромагнитная нержавеющая сталь 410, магнитная проницаемость 1000 и удельное сопротивление = 5,7⋅10^-7 Ом·м.
Fe-Si – текстурированная электротехническая сталь (состав около 97% Fe и 3% Si), проницаемость = 29000 и удельное сопротивление = 5,0⋅10^-8 Ом·м.
Fe-Ni – пермаллой (торговое наименование VACUUMSCHMELZE GmbH & Co. KG - Mumetall), проницаемость = 250 000 и удельное сопротивления = 5,5⋅10^-7 Ом·м.
Красной вертикальной прямой отмечена частота 50 Гц.

Плотность тока максимальна у поверхности проводника. При удалении от поверхности она убывает экспоненциально и на глубине [math]\displaystyle{ \delta }[/math] становится меньше в е раз (примерно на 70 %). Эта глубина называется толщиной скин-слоя и на основании приведённого выше равна:

[math]\displaystyle{ \Delta = \sqrt{\frac{2}{\gamma \mu \omega}}. }[/math]

Толщина скин-слоя в меди

Частота	[math]\displaystyle{ \delta, }[/math] мм	Примечания
50 Гц	9,34 мм	50 Гц — частота электросети в большинстве стран Евразии и Африки
60 Гц	8,53 мм	60 Гц — частота электросети в Северной, Центральной и частично Южной Америке
10 кГц	0,66 мм
100 кГц	0,21 мм
500 кГц	0,095 мм
1 МГц	0,067 мм
10 МГц	0,021 мм

Очевидно, что при достаточно большой частоте [math]\displaystyle{ \omega }[/math] толщина скин-слоя может быть очень малой. Также из экспоненциального убывания плотности тока следует, что практически весь ток сосредоточен в слое толщиной в несколько [math]\displaystyle{ \delta }[/math], так, уменьшение плотности тока в 100 раз происходит на глубине [math]\displaystyle{ \approx \text{4,6}\ \delta }[/math], если общая толщина проводника многократно превышает толщину скин-слоя. В качестве примера в таблице приведена зависимость толщины скин-слоя от частоты для медного проводника.

Если проводник имеет ферромагнитные свойства, то толщина скин-слоя будет во много раз меньше. Например, для стали ([math]\displaystyle{ \mu_m\ }[/math]= 1000) [math]\displaystyle{ \delta\ }[/math]= 0,74 мм. Это имеет значение, например, при электрификации железных дорог, поскольку там стальные рельсы используются в качестве обратного провода.

Для расчёта толщины скин-слоя в металле можно использовать следующие приближённые формулы:

[math]\displaystyle{ \Delta=c \sqrt{2\frac{\varepsilon_0}{\omega\mu_m}\rho}, }[/math]

здесь [math]\displaystyle{ \ \varepsilon_0 }[/math] = 8,85419⋅10⁻¹² Ф/м — электрическая постоянная, [math]\displaystyle{ \ \rho }[/math] — удельное сопротивление, [math]\displaystyle{ \ c }[/math] — скорость света, [math]\displaystyle{ \ \mu_m }[/math] — относительная магнитная проницаемость (близка к единице для пара- и диамагнетиков — меди, серебра, и т. п.), [math]\displaystyle{ \ \omega=2\pi \cdot f,\ \ }[/math] [math]\displaystyle{ \ f\ }[/math] — частота.

Все величины выражены в системе СИ.

Практически удобная формула:

[math]\displaystyle{ \Delta=503\sqrt{\frac{\rho}{\mu_m f}}. }[/math]

Аномальный скин-эффект

Изложенная теория справедлива лишь при условии, что толщина скин-слоя много больше средней длины свободного пробега электронов, так как мы предполагаем, что при своём движении электрон непрерывно теряет энергию на преодоление омического сопротивления проводника, в результате чего происходит выделение джоулевой теплоты. Такое соотношение справедливо в весьма широких пределах, однако даже при комнатной температуре длина свободного пробега электрона для металлов сопоставима с глубиной скин-слоя — что говорит об аномальном характере эффекта. При очень низкой температуре ситуация только усугубляется: проводимость сильно повышается, а следовательно, увеличивается длина свободного пробега и уменьшается толщина скин-слоя. При этих условиях механизм, приводящий к образованию скин-эффекта, уже не действует. Эффективная толщина слоя, в котором сосредоточен ток, изменяется. Такое явление называется аномальным скин-эффектом.

Применение

На скин-эффекте основано действие взрывомагнитных генераторов (ВМГ), взрывомагнитных генераторов частоты (ВМГЧ) и в частности ударно-волновых излучателей (УВИ).

Благодаря скин-эффекту, в высокочастотном магнитном поле теплота выделяется преимущественно в поверхностном слое. Это позволяет нагревать проводник в тонком поверхностном слое без существенного изменения температуры внутренних областей. Это явление используется в важном, с промышленной точки зрения, методе поверхностной закалки металлов, реализуемом на основе индукционного нагрева.

Помимо поверхностной закалки, в индукционном нагреве скин-эффект позволяет реализовать технологию индукционного удаления полимерных покрытий, широко используемую при ремонте магистральных нефте- и газопроводов, ремонте палубных покрытий морских судов и т. п.

Учёт эффекта в технике и борьба с ним

Скин-эффект проявляется существеннее с увеличением частоты переменного тока, и учитывается при конструировании и расчётах электрических схем, работающих на переменном и импульсном токах. Так как ток высокой частоты течёт по тонкому поверхностному слою проводника, общее активное сопротивление проводника возрастает, что приводит к быстрому затуханию колебаний высокой частоты.

Скин-эффект влияет на характеристики катушек индуктивности и колебательных контуров, такие как добротность, на затухание в линиях передачи, на характеристики фильтров, на расчёты тепловых потерь и КПД, на выбор сечений проводников.

Для уменьшения влияния скин-эффекта применяют проводники различного сечения: плоские (в виде лент), трубчатые (полые внутри), наносят на поверхность проводника слой металла с более низким удельным сопротивлением. Например, серебро обладает наибольшей удельной проводимостью среди всех металлов и технологично для нанесения на металлические поверхности. Тонкий его слой, в котором из-за скин-эффекта и протекает бо́льшая часть тока, оказывает заметное снижение (до 10 %) активного сопротивления проводника. Однако, слой сульфида, образующийся на поверхности серебра, не проводит ток и не участвует в скин-эффекте, в отличие от слоя окиси-закиси на поверхности меди, обладающего заметной проводимостью, и имеет свойства полупроводника, и вносит дополнительные потери на высоких частотах.

Покрытие серебром также применяется в сверхвысокочастотном оборудовании, использующем колебательные контуры особой формы: объёмные резонаторы и специфические линии передачи — волноводы. Кроме того, на таких частотах уделяют внимание снижению шероховатости поверхности с целью уменьшения длины пути протекания тока.

Также применяется и покрытие золотом, у которого слой окислов отсутствует. Напротив, покрытие никелем, оловом или оловянно-свинцовым припоем способно значительно, в несколько раз увеличить сопротивление медных проводников на высоких частотах.

Так, в ВЧ аппаратуре используют катушки индуктивности, намотанные из посеребрённого провода, часто серебрят печатные и проволочные проводники, поверхности экранов и обкладки конденсаторов. В высоковольтных линиях электропередач иногда применяют провод в медной, либо алюминиевой оболочке со стальным сердечником, в мощных генераторах переменного тока обмотка изготавливается из трубок, по которым для охлаждения циркулирует дистиллированная вода.

Также с целью снижения скин-эффекта используют систему из нескольких переплетённых и изолированных проводов — намоточный провод литцендрат.

При передаче больших мощностей на значительные расстояния применяются линии электропередачи постоянного тока — HVDC, постоянный ток не вызывает скин-эффект.

Литература

• Матвеев А. Н. Параграф 53 // Электричество и магнетизм. — М.: Высшая школа, 1983. — 463 с.
• Власов A. A. Глава VI. Параграф 5 // Макроскопическая электродинамика. — 2-е изд.. — М.: Наука, 2005.