Удельное электрическое сопротивление

Удельное электрическое сопротивление
[math]\displaystyle{ \rho }[/math]
Размерность	СИ:L3MT-3I-2 СГС:T
Единицы измерения
СИ	Ом·метр
СГС	с

Уде́льное электри́ческое сопротивле́ние ρ — способность материала препятствовать прохождению электрического тока, Ом·метр на величину объема ("удельное", берем кубический метр вещества и смотрим как этот кубический объем вещества проводит электрический ток).

ρ зависит от температуры в различных материалах по-разному: в проводниках удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается. Величина, учитывающая изменение электрического сопротивления от температуры, называется температурный коэффициент удельного сопротивления. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.

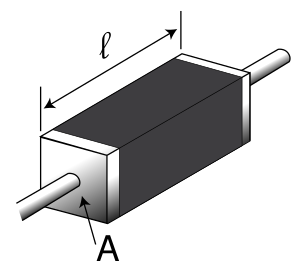
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле [math]\displaystyle{ R=\frac{\rho \cdot l}{S} }[/math] (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется [math]\displaystyle{ \rho =\frac{R \cdot S}{l}. }[/math]

Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения .

Единицы измерения

Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м. Из соотношения [math]\displaystyle{ \rho =\frac{R \cdot S}{l} }[/math] следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².

В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10⁻⁶ от 1 Ом·м. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².

Зависимость от температуры

В проводниках удельное электрическое сопротивление увеличивается с увеличением температуры. Это объясняется тем, что с ростом температуры увеличивается интенсивность колебания атомов в узлах кристаллической решетки проводника, что препятствует движению свободных электронов.

В полупроводниках и диэлектриках удельное электрическое сопротивление уменьшается. Это объясняется тем, что с увеличением температуры увеличивается концентрация основных носителей заряда.

Величина, учитывающая изменение удельного электрического сопротивление от температуры называют температурным коэффициентом удельного сопротивления.

Обобщение понятия удельного сопротивления

Кусок резистивного материала с электрическими контактами на обоих концах

Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля [math]\displaystyle{ \vec{E}(\vec{r}) }[/math] и плотность тока [math]\displaystyle{ \vec{J}(\vec{r}) }[/math] в данной точке [math]\displaystyle{ \vec{r} }[/math]. Указанная связь выражается законом Ома в дифференциальной форме:

[math]\displaystyle{ \vec{E}(\vec{r}) = \rho(\vec{r})\vec{J}(\vec{r}). }[/math]

Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент [math]\displaystyle{ \rho_{ij} }[/math]. В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением

[math]\displaystyle{ E_i(\vec{r}) = \sum_{j=1}^3\rho_{ij}(\vec{r})J_j(\vec{r}). }[/math]

В анизотропном, но однородном веществе тензор [math]\displaystyle{ \rho_{ij} }[/math] от координат не зависит.

Тензор [math]\displaystyle{ \rho_{ij} }[/math] симметричен, то есть для любых [math]\displaystyle{ i }[/math] и [math]\displaystyle{ j }[/math] выполняется [math]\displaystyle{ \rho_{ij} = \rho_{ji} }[/math].

Как и для всякого симметричного тензора, для [math]\displaystyle{ \rho_{ij} }[/math] можно выбрать ортогональную систему декартовых координат, в которых матрица [math]\displaystyle{ \rho_{ij} }[/math] становится диагональной, то есть приобретает вид, при котором из девяти компонент [math]\displaystyle{ \rho_{ij} }[/math] отличными от нуля являются лишь три: [math]\displaystyle{ \rho_{11} }[/math], [math]\displaystyle{ \rho_{22} }[/math] и [math]\displaystyle{ \rho_{33} }[/math]. В этом случае, обозначив [math]\displaystyle{ \rho_{ii} }[/math] как [math]\displaystyle{ \rho_i }[/math], вместо предыдущей формулы получаем более простую

[math]\displaystyle{ E_i = \rho_i J_i. }[/math]

Величины [math]\displaystyle{ \rho_i }[/math] называют главными значениями тензора удельного сопротивления.

Связь с удельной проводимостью

В изотропных материалах связь между удельным сопротивлением [math]\displaystyle{ \rho }[/math] и удельной проводимостью [math]\displaystyle{ \sigma }[/math] выражается равенством

[math]\displaystyle{ \rho = \frac{1}{\sigma}. }[/math]

В случае анизотропных материалов связь между компонентами тензора удельного сопротивления [math]\displaystyle{ \rho_{ij} }[/math] и тензора удельной проводимости [math]\displaystyle{ \sigma_{ij} }[/math] имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:

[math]\displaystyle{ J_i(\vec{r}) = \sum_{j=1}^3\sigma_{ij}(\vec{r})E_j(\vec{r}). }[/math]

Из этого равенства и приведённого ранее соотношения для [math]\displaystyle{ E_i(\vec{r}) }[/math] следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:

[math]\displaystyle{ \rho_{11} = \frac{1}{\det(\sigma)}[\sigma_{22}\sigma_{33} - \sigma_{23}\sigma_{32}], }[/math]

[math]\displaystyle{ \rho_{12} = \frac{1}{\det(\sigma)}[\sigma_{33}\sigma_{12} - \sigma_{13}\sigma_{32}], }[/math]

где [math]\displaystyle{ \det(\sigma) }[/math] — определитель матрицы, составленной из компонент тензора [math]\displaystyle{ \sigma_{ij} }[/math]. Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3.

Удельное электрическое сопротивление некоторых веществ

Металлические монокристаллы

В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C.

Кристалл	ρ1=ρ2, 10−8 Ом·м	ρ3, 10−8 Ом·м
Олово	9,9	14,3
Висмут	109	138
Кадмий	6,8	8,3
Цинк	5,91	6,13
Теллур	2,90·109	5,9·109

Металлы и сплавы, применяемые в электротехнике

Разброс значений обусловлен разной химической чистотой металлов, способами изготовления образцов, изученных разными учеными, и непостоянством состава сплавов.

Металл ρ, Ом·мм²/м Серебро 0,015…0,0162 Медь 0,01707…0,018 Медь 6N Cu 99.9999% 0,01673 Золото 0,023 Алюминий 0,0262…0,0295 Иридий 0,0474 Натрий 0,0485 Молибден 0,054 Вольфрам 0,053…0,055 Цинк 0,059 Индий 0,0837 Никель 0,087 Железо 0,099 Платина 0,107 Олово 0,12 Свинец 0,217…0,227 Титан 0,5562…0,7837 Ртуть 0,958 Висмут 1,2

Сплав ρ, Ом·мм²/м Сталь 0,103…0,137 Никелин 0,42 Константан 0,5 Манганин 0,43…0,51 Нихром 1,05…1,4 Фехраль 1,15…1,35 Хромель 1,3…1,5 Латунь 0,025…0,108 Бронза 0,095…0,1

Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.

Другие вещества

Вещество	ρ, Ом·мм²/м
Сжиженные углеводородные газы	0,84⋅1010

Тонкие плёнки

Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», [math]\displaystyle{ R_\mathrm{Sq}. }[/math] Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: [math]\displaystyle{ R_\mathrm{Sq}=R W/L, }[/math] где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в плёнке неоднородное, используют метод ван дер Пау.

См. также

• Электрическое сопротивление
• Сверхпроводимость
• Закон Ома
• Удельная проводимость
• Отрицательное сопротивление
• Импеданс
• Температурный коэффициент электрического сопротивления

Литература

• Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд., переработанное и дополненное. — М.: Высшая школа, 1986. — С. 6—7. — 208 с.