Длина свободного пробега
Длина свободного пробега молекулы — это среднее расстояние [math]\displaystyle{ \lambda }[/math], которое пролетает частица за время между двумя последовательными столкновениями.[1]
Для каждой молекулы это расстояние различно, поэтому в кинетической теории газов под длиной свободного пробега обычно подразумевается[2] средняя длина свободного пробега <[math]\displaystyle{ \lambda }[/math]>, которая является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры.
Теория рассеяния
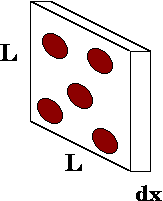
Представим поток частиц, проходящих через мишень размером [math]\displaystyle{ L \times L }[/math], и рассмотрим бесконечно тонкий слой этой мишени (см. рисунок).[3] Красным здесь обозначены атомы, с которыми частицы падающего пучка могут столкнуться. Значение длины свободного пробега будет зависеть от характеристик этой системы. Если все частицы мишени покоятся, то выражение для длины свободного пробега будет выглядеть как:
- [math]\displaystyle{ \ell = (\sigma n)^{-1}, }[/math]
где n — количество частиц мишени в единице объёма, а σ — эффективное сечение.
Площадь такого слоя L2, объём L2 dx, и тогда количество неподвижных атомов в нём n L2 dx. Вероятность [math]\displaystyle{ dP }[/math] рассеяния этим слоем одной частицы равна отношению части площади сечения, «перекрываемой» всеми рассеивающими частицами, ко всей площади сечения:
- [math]\displaystyle{ dP = \frac{\sigma n L^{2}\, dx}{L^{2}} = n \sigma\, dx, }[/math] где σ — площадь, или, более точно, сечение рассеяния одного атома.
Тогда уменьшение [math]\displaystyle{ dI }[/math] интенсивности потока будет равно начальной интенсивности, умноженной на вероятность рассеяния частицы внутри мишени:
- [math]\displaystyle{ dI = -I n \sigma \,dx. }[/math]
Получаем дифференциальное уравнение
- [math]\displaystyle{ \frac{dI}{dx} = -I n \sigma = -\frac{I}{\ell}, }[/math]
решение которого известно как закон закон Бугера[4] и имеет вид [math]\displaystyle{ I = I_{0} e^{-x/\ell} }[/math], где x — расстояние, пройденное пучком, I0 — интенсивность пучка до того, как он попал в мишень, а ℓ называется средней длиной свободного пробега, потому что она равна среднему расстоянию, пройденному частицей пучка до остановки. Чтобы убедиться в этом, обратим внимание, что вероятность того, что частица будет рассеяна в слое от x до x + dx, равна
- [math]\displaystyle{ dP(x) = \frac{I(x)-I(x+dx)}{I_0} = \frac{1}{\ell} e^{-x/\ell} dx. }[/math]
И таким образом, среднее значение x будет равно
- [math]\displaystyle{ \langle x \rangle = \int_0^\infty x dP(x) = \int_0^\infty \frac{x}{\ell} e^{-x/\ell} \, dx = \ell. }[/math]
Отношение части частиц, которые не рассеялись мишенью, к количеству, падающему на её поверхность, называется коэффициентом пропускания [math]\displaystyle{ T = I/I_{0} = e^{-x/\ell} }[/math], где x = dx — толщина мишени
Кинетическая теория
В кинетической теории газов длина свободного пробега частицы (например, молекулы) — это среднее расстояние, которое проходит частица за время между столкновениями с другими движущимися частицами. В приведенном выше выводе предполагалось, что частицы-мишени находятся в состоянии покоя, поэтому формула [math]\displaystyle{ \ell = (n\sigma)^{-1} }[/math], вообще говоря, справедлива только для падающих частиц со скоростями, высокими относительно скоростей совокупности таких же частиц со случайным расположением. В этом случае движения частиц мишени будут незначительны, а относительная скорость примерно равна скорости частицы.
Если же частица пучка является частью установившейся равновесной системы с идентичными частицами, то квадрат относительной скорости равен:
[math]\displaystyle{ \overline{\mathbf{v}_{\rm relative}^2}=\overline{(\mathbf{v}_1-\mathbf{v}_2)^2} =\overline{\mathbf{v}_1^2+\mathbf{v}_2^2-2\mathbf{v}_1 \cdot \mathbf{v}_2}. }[/math]
В состоянии равновесия значения скоростей [math]\displaystyle{ \mathbf{v}_1 }[/math] и [math]\displaystyle{ \mathbf{v}_2 }[/math] случайны и независимы, поэтому [math]\displaystyle{ \overline{\mathbf{v}_1 \cdot \mathbf{v}_2}=0 }[/math], а относительная скорость равна
[math]\displaystyle{ v_{\rm rel}=\sqrt{\overline{\mathbf{v}_{\rm relative}^2}} =\sqrt{\overline{\mathbf{v}_1^2+\mathbf{v}_2^2}} =\sqrt{2}v. }[/math]
Это означает, что количество столкновений равно [math]\displaystyle{ \sqrt{2} }[/math], умноженному на количество неподвижных целей. Следовательно, применимо следующее соотношение:[5]
[math]\displaystyle{ \ell = (\sqrt{2}\, n\sigma)^{-1} }[/math]
Из закона Менделеева-Клапейрона [math]\displaystyle{ n = N/V = p/(k_\text{B}T) }[/math] и с учётом [math]\displaystyle{ \sigma = \pi (2r)^2 = \pi d^2 }[/math] (эффективная площадь поперечного сечения для сферических частиц радиусом [math]\displaystyle{ r }[/math]) можно показать, что длина свободного пробега равна[6]
- [math]\displaystyle{ \ell = \frac{k_\text{B}T}{\sqrt 2 \pi d^2 p}, }[/math] где kB — постоянная Больцмана.
На практике диаметр молекул газа не определён точно. Фактически, кинетический диаметр молекулы определяется через длину свободного пробега. Как правило, молекулы газа не ведут себя как твердые сферы, а скорее притягиваются друг к другу на больших расстояниях и отталкиваются друг от друга на меньших, что можно описать с помощью потенциала Леннарда-Джонса. Один из способов описать такие «мягкие» молекулы — использовать параметр σ Леннарда-Джонса в качестве диаметра. Другой способ — предположить, что газ в модели твердых сфер имеет ту же вязкость, что и рассматриваемый реальный газ. Это приводит к средней длине свободного пробега[7]
- [math]\displaystyle{ \ell = \frac{\mu}{p} \sqrt{\frac{\pi k_\text{B} T}{2 m}}, }[/math]
где m — масса молекулы, а μ — вязкость. Это выражение можно удобно представить в следующем виде:
- [math]\displaystyle{ \ell = \frac{\mu}{p} \sqrt{\frac{\pi R_u T}{2 M}}, }[/math]
где [math]\displaystyle{ R_u }[/math] — универсальная газовая постоянная, а [math]\displaystyle{ M }[/math] — молекулярная масса. Эти разные определения диаметра молекулы могут привести к немного разным значениям длины свободного пробега.
Формула
- [math]\displaystyle{ \lambda = \frac{1}{\sqrt{2} \sigma n} }[/math], где [math]\displaystyle{ \sigma }[/math] — эффективное сечение молекулы, равное [math]\displaystyle{ {\pi d^2} }[/math] ([math]\displaystyle{ d }[/math] — эффективный диаметр молекулы), а [math]\displaystyle{ n }[/math] — концентрация молекул.
Примеры
В следующей таблице приведены типичные значения длины свободного пробега молекул воздуха при комнатной температуре для различных давлений.
| Диапазон давления | Давление, Па | Давление, мм.рт.ст. | Концентрация, молекул / см3 | Концентрация, молекул / м3 | Длина свободного пробега |
|---|---|---|---|---|---|
| Атмосферное давление | 101300 | 759.8 | 2.7 × 1019 | 2.7 × 1025 | 68[8] нм |
| Низкий вакуум | 30000 — 100 | 220 — 8×10−1 | 1019 — 1016 | 1025 — 1022 | 0.1 — 100 мкм |
| Средний вакуум | 100 — 10−1 | 8×10−1 — 8×10−4 | 1016 — 1013 | 1022 — 1019 | 0.1 — 100 мм |
| Высокий вакуум | 10−1 — 10−5 | 8×10−4 — 8×10−8 | 1013 — 109 | 1019 — 1015 | 10 см- 1 км |
| Сверхвысокий вакуум | 10−5 — 10−10 | 8×10−8 — 8×10−13 | 109 — 104 | 1015 — 1010 | 1 km — 105 km |
| Экстремальный вакуум | <10−10 | <8×10−13 | <104 | <1010 | >105 km |
См. также
Примечания
- ↑ Marion Brünglinghaus. Mean free path. Euronuclear.org.
- ↑ Алешкевич В.А. Курс общей физики. Молекулярная физика.. — М.: ФИЗМАТЛИТ, 2016. — С. 281—283. — 312 с. — ISBN 978-5-9221-1696-1.
- ↑ Chen, Frank F. Introduction to Plasma Physics and Controlled Fusion. — 1st. — Plenum Press, 1984. — P. 156. — ISBN 0-306-41332-9.
- ↑ Сивухин Д.В. Общий курс физики // Поглощение света и уширение спектральных линий. — Москва, 2005. — С. 582—583. — 792 с. — ISBN ISBN 5-9221-0228-1.
- ↑ S. Chapman and T. G. Cowling, The mathematical theory of non-uniform gases Архивная копия от 7 ноября 2020 на Wayback Machine, 3rd. edition, Cambridge University Press, 1990, ISBN 0-521-40844-X, p. 88.
- ↑ Mean Free Path, Molecular Collisions. Hyperphysics.phy-astr.gsu.edu. Дата обращения: 8 ноября 2011. Архивировано 28 октября 2011 года.
- ↑ Vincenti, W. G. and Kruger, C. H. Introduction to physical gas dynamics. — Krieger Publishing Company, 1965. — P. 414.
- ↑ S.G Jennings. The mean free path in air (англ.) // Journal of Aerosol Science. — 1988-04. — Vol. 19, iss. 2. — P. 159–166. — doi:10.1016/0021-8502(88)90219-4. Архивировано 8 марта 2021 года.
Ссылки
- Длина свободного пробега — статья из Физической энциклопедии