Образ (математика)

Образ функции — это множество всех значений, которые даёт функция.
В более общем виде, вычисление значения заданной функции [math]\displaystyle{ f }[/math] для каждого элемента заданного подмножества [math]\displaystyle{ A }[/math] области определения функции даёт множество, называемое «образом [math]\displaystyle{ A }[/math] для функции [math]\displaystyle{ f }[/math]». Аналогично, обратный образ (или прообраз) заданного подмножества [math]\displaystyle{ B }[/math] кодомена функции [math]\displaystyle{ f }[/math] — это множество всех элементов области определения, которые отображаются в элементы множества [math]\displaystyle{ B }[/math].
Образ и обратный образ могут также быть определены для общих бинарных отношений, а не только функций.
Определение
Слово «образ» используется тремя связанными способами. В этих определениях [math]\displaystyle{ f\colon X \to Y }[/math] — это функция из множества [math]\displaystyle{ X }[/math] в множество [math]\displaystyle{ Y }[/math].
Образ элемента
Если [math]\displaystyle{ x }[/math] является элементом множества [math]\displaystyle{ X }[/math], то образ элемента [math]\displaystyle{ x }[/math] для функции [math]\displaystyle{ f }[/math], обозначаемый [math]\displaystyle{ f(x) }[/math][1], — это значение функции [math]\displaystyle{ f }[/math] для аргумента [math]\displaystyle{ x }[/math].
Образ подмножества
Образ подмножества [math]\displaystyle{ A \subseteq X }[/math] для функции [math]\displaystyle{ f }[/math], обозначаемый [math]\displaystyle{ f[A] }[/math], является подмножеством множества [math]\displaystyle{ Y }[/math], которое может быть определено с помощью следующей формы записи[2]:
- [math]\displaystyle{ f[A] = \{ f(x) \mid x \in A \} }[/math]
Если нет риска путаницы, [math]\displaystyle{ f[A] }[/math] записывается просто как [math]\displaystyle{ f(A) }[/math]. Это соглашение является общепринятым. Предполагаемый смысл должен быть определён из контекста. Это делает f[.] функцией, областью определения которой является степень множества X (множество всех подмножеств множества X), а кодоменом является степень множества Y. См. раздел § Обозначения.
Образ функции
Образ функции — это образ всей области определения, известный также как область значений функции[3].
Обобщение к бинарным отношениям
Если [math]\displaystyle{ R }[/math] является произвольным бинарным отношением на X[math]\displaystyle{ \times }[/math]Y, то множество [math]\displaystyle{ \{ y \in Y \| xRy, x \in X \} }[/math] называется образом отношения [math]\displaystyle{ R }[/math]. Множество [math]\displaystyle{ \{ x\in X | xRy, y \in Y\} }[/math] называется областью определения отношения [math]\displaystyle{ R }[/math].
Обратный образ
Пусть [math]\displaystyle{ f }[/math] будет функцией из [math]\displaystyle{ X }[/math] в [math]\displaystyle{ Y }[/math]. Прообраз или обратный образ множества [math]\displaystyle{ B \subseteq Y }[/math] для функции [math]\displaystyle{ f }[/math], обозначаемый [math]\displaystyle{ f^{-1}[B] }[/math], — это подмножество [math]\displaystyle{ X }[/math] определённое как:
- [math]\displaystyle{ f^{-1}[ B ] = \{ x \in X \, | \, f(x) \in B \}. }[/math]
Возможны и другие обозначения, как, например: [math]\displaystyle{ f^{-1}(B) }[/math][4] и [math]\displaystyle{ f^-(B) }[/math].[5]
Обратный образ синглтона, обозначаемый [math]\displaystyle{ f^{-1}[\{y\}] }[/math] или [math]\displaystyle{ f^{-1}[y] }[/math], называется также слоем для [math]\displaystyle{ y }[/math] или множеством уровня элемента [math]\displaystyle{ y }[/math]. Множество всех слоёв для элементов [math]\displaystyle{ Y }[/math] — это семейство подмножеств, индексированных элементами [math]\displaystyle{ Y }[/math].
Например, для функции [math]\displaystyle{ f(x) = x^2 }[/math] обратным образом [math]\displaystyle{ \{4\} }[/math] будет [math]\displaystyle{ \{-2, 2\} }[/math]. Снова, если нет риска путаницы, [math]\displaystyle{ f^{-1}[B] }[/math] может обозначаться как [math]\displaystyle{ f^{-1}(B) }[/math], а [math]\displaystyle{ f^{-1} }[/math] можно рассматривать как функцию из множества всех подмножеств (булеана) множества [math]\displaystyle{ Y }[/math] в булеан множества [math]\displaystyle{ X }[/math]. Обозначение [math]\displaystyle{ f^{-1} }[/math] не следует путать с обратной функцией, хотя оно и согласуется с обычной обратной функцией для биекций в том, что обратный образ [math]\displaystyle{ B }[/math] для [math]\displaystyle{ f }[/math] является образом [math]\displaystyle{ B }[/math] для [math]\displaystyle{ f^{-1} }[/math].
Обозначения для образа и обратного образа
Традиционные обозначения, использованные в предыдущих разделах, могут вызвать сложности в понимании. Альтернативой[6] является задание явных имён для образа и прообраза функций между булеанами:
Стрелочные обозначения
- [math]\displaystyle{ f^\to:\mathcal{P}(X)\to\mathcal{P}(Y) }[/math] для [math]\displaystyle{ f^\to(A) = \{ f(a)\;|\; a \in A\} }[/math]
- [math]\displaystyle{ f^\leftarrow:\mathcal{P}(Y)\to\mathcal{P}(X) }[/math] для [math]\displaystyle{ f^\leftarrow(B) = \{ a \in X \;|\; f(a) \in B\} }[/math]
Обозначения со звёздочками
- [math]\displaystyle{ f_\star:\mathcal{P}(X)\to\mathcal{P}(Y) }[/math] вместо [math]\displaystyle{ f^\to }[/math]
- [math]\displaystyle{ f^\star:\mathcal{P}(Y)\to\mathcal{P}(X) }[/math] вместо [math]\displaystyle{ f^\leftarrow }[/math]
Другая терминология
- Альтернативные обозначения [math]\displaystyle{ f[A] }[/math], используемые в математической логике и теории множеств, это [math]\displaystyle{ f^{\prime\prime}A }[/math][7][8].
- Некоторые книги называют образ [math]\displaystyle{ f }[/math] областью значений [math]\displaystyle{ f }[/math], но этого следует избегать, поскольку термин «область значений» используется широко также для обозначения кодомена функции [math]\displaystyle{ f }[/math].
Примеры
- [math]\displaystyle{ f\colon \{1, 2, 3\} \to \{a, b, c, d\} }[/math] определена как [math]\displaystyle{ f(x) = \left\{\begin{matrix} a, & \mbox{ если } x=1 \\ a, & \mbox{ если } x=2 \\ c, & \mbox{ если } x=3. \end{matrix}\right. }[/math] Образом множества {2, 3} для функции [math]\displaystyle{ f }[/math] является [math]\displaystyle{ f(\{2, 3\}) = \{a, c\} }[/math]. Образ функции [math]\displaystyle{ f }[/math] — это [math]\displaystyle{ \{a, c\} }[/math]. Прообразом [math]\displaystyle{ a }[/math] является [math]\displaystyle{ f^{-1}(\{a\}) = \{1, 2\} }[/math]. Прообразом множества [math]\displaystyle{ \{a, b\} }[/math] также является [math]\displaystyle{ \{1, 2\} }[/math]. Прообразом множества [math]\displaystyle{ \{b, d\} }[/math] является пустое множество [math]\displaystyle{ \{\} }[/math].
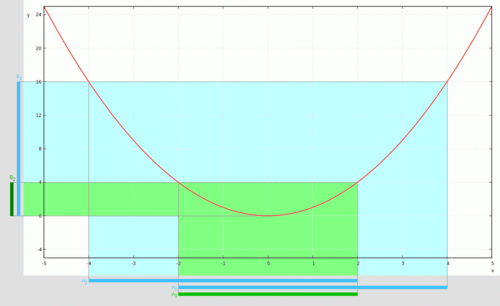
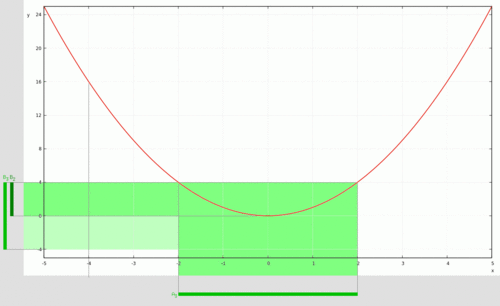
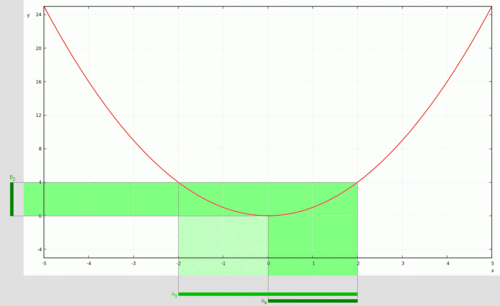
- [math]\displaystyle{ f\colon \mathbf{R} \to \mathbf{R} }[/math] определена как [math]\displaystyle{ f(x) = x^2 }[/math]. Образ [math]\displaystyle{ \{-2, 3\} }[/math] для функции [math]\displaystyle{ f }[/math] — это [math]\displaystyle{ f(\{-2, 3\}) = \{4, 9\} }[/math], а образ функции [math]\displaystyle{ f }[/math] — это [math]\displaystyle{ \mathbf{R}^+ }[/math]. Прообраз [math]\displaystyle{ \{4, 9\} }[/math] для [math]\displaystyle{ f }[/math] — это [math]\displaystyle{ f^{-1}(\{4, 9\}) = \{-3, -2, 2, 3\} }[/math]. Прообраз множества [math]\displaystyle{ N = \{n \in \mathbf{R} \| n \lt 0\} }[/math] для [math]\displaystyle{ f }[/math] — это пустое множество, поскольку отрицательные числа не имеют квадратных корней в множестве вещественных чисел.
- [math]\displaystyle{ f\colon \mathbf{R}^2 \to \mathbf{R} }[/math] определена как [math]\displaystyle{ f(x, y) = x^2 + y^2 }[/math]. Слои [math]\displaystyle{ f^{-1}(\{a\}) }[/math] являются концентричными окружностями вокруг начала координат, единственная точка начала координат или пустого множества в зависимости от того, [math]\displaystyle{ a \gt 0 }[/math], [math]\displaystyle{ a = 0 }[/math] или [math]\displaystyle{ a \lt 0 }[/math] соответственно.
- Если [math]\displaystyle{ M }[/math] — это многообразие, а [math]\displaystyle{ \pi: TM \to M }[/math] — это каноническая проекция из касательного расслоения [math]\displaystyle{ TM }[/math] в [math]\displaystyle{ M }[/math], то слоями отображения [math]\displaystyle{ \pi }[/math] являются касательные пространства [math]\displaystyle{ T_x(M) }[/math] для [math]\displaystyle{ x \in M }[/math]. Это также пример расслоённого пространства.
- Факторгруппа — это гомоморфный образ.
Свойства
Контрпримеры
Общий случай
Для любой функции [math]\displaystyle{ f \colon X \to Y }[/math] и всех подмножеств [math]\displaystyle{ A \subseteq X }[/math] и [math]\displaystyle{ B \subseteq Y }[/math] выполняются следующие свойства:
| Образ | Прообраз |
|---|---|
| [math]\displaystyle{ f(X) \subseteq Y }[/math] | [math]\displaystyle{ f^{-1}(Y) = X }[/math] |
| [math]\displaystyle{ f(f^{-1}(Y)) = f(X) }[/math] | [math]\displaystyle{ f^{-1}(f(X)) = X }[/math] |
| [math]\displaystyle{ f(f^{-1}(B)) \subseteq B }[/math] (равны, если [math]\displaystyle{ B \subseteq f(X) }[/math], т.е. [math]\displaystyle{ f }[/math] сюръектвна)[9][10] |
[math]\displaystyle{ f^{-1}(f(A)) \supseteq A }[/math] (равны, если [math]\displaystyle{ f }[/math] инъективна) [9][10] |
| [math]\displaystyle{ f(f^{-1}(B)) = B \cap f(X) }[/math] | [math]\displaystyle{ (f \vert_A)^{-1}(B) = A \cap f^{-1}(B) }[/math] |
| [math]\displaystyle{ f(f^{-1}(f(A))) = f(A) }[/math] | [math]\displaystyle{ f^{-1}(f(f^{-1}(B))) = f^{-1}(B) }[/math] |
| [math]\displaystyle{ f(A) = \varnothing \Leftrightarrow A = \varnothing }[/math] | [math]\displaystyle{ f^{-1}(B) = \varnothing \Leftrightarrow B \subseteq Y \setminus f(X) }[/math] |
| [math]\displaystyle{ f(A) \supseteq B \Leftrightarrow \exists C \subseteq A : f(C) = B }[/math] | [math]\displaystyle{ f^{-1}(B) \supseteq A \Leftrightarrow f(A) \subseteq B }[/math] |
| [math]\displaystyle{ f(A) \supseteq f(X \setminus A) \Leftrightarrow f(A) = f(X) }[/math] | [math]\displaystyle{ f^{-1}(B) \supseteq f^{-1}(Y \setminus B) \Leftrightarrow f^{-1}(B) = X }[/math] |
| [math]\displaystyle{ f(X \setminus A) \supseteq f(X) \setminus f(A) }[/math] | [math]\displaystyle{ f^{-1}(Y \setminus B) = X \setminus f^{-1}(B) }[/math][9] |
| [math]\displaystyle{ f(A \cup f^{-1}(B)) \subseteq f(A) \cup B }[/math][11] | [math]\displaystyle{ f^{-1}(f(A) \cup B) \supseteq A \cup f^{-1}(B) }[/math][11] |
| [math]\displaystyle{ f(A \cap f^{-1}(B)) = f(A) \cap B }[/math][11] | [math]\displaystyle{ f^{-1}(f(A) \cap B) \supseteq A \cap f^{-1}(B) }[/math][11] |
Также:
- [math]\displaystyle{ f(A) \cap B = \varnothing \Leftrightarrow A \cap f^{-1}(B) = \varnothing }[/math]
Для нескольких функций
Для функций [math]\displaystyle{ f\colon X \to Y }[/math] и [math]\displaystyle{ g\colon Y \to Z }[/math] с подмножествами [math]\displaystyle{ A \subseteq X }[/math] и [math]\displaystyle{ C \subseteq Z }[/math] выполняются следующие свойства:
- [math]\displaystyle{ (g \circ f)(A) = g(f(A)) }[/math]
- [math]\displaystyle{ (g \circ f)^{-1}(C) = f^{-1}(g^{-1}(C)) }[/math]
Несколько подмножеств домена или кодомена
Для функции [math]\displaystyle{ f\colon X \to Y }[/math] и подмножеств [math]\displaystyle{ A_1,A_2 \subseteq X }[/math] и [math]\displaystyle{ B_1,B_2 \subseteq Y }[/math] выполняются следующие свойства:
| Образ | Прообраз |
|---|---|
| [math]\displaystyle{ A_1 \subseteq A_2 \Rightarrow f(A_1) \subseteq f(A_2) }[/math] | [math]\displaystyle{ B_1 \subseteq B_2 \Rightarrow f^{-1}(B_1) \subseteq f^{-1}(B_2) }[/math] |
| [math]\displaystyle{ f(A_1 \cup A_2) = f(A_1) \cup f(A_2) }[/math][11][12] | [math]\displaystyle{ f^{-1}(B_1 \cup B_2) = f^{-1}(B_1) \cup f^{-1}(B_2) }[/math] |
| [math]\displaystyle{ f(A_1 \cap A_2) \subseteq f(A_1) \cap f(A_2) }[/math][11][12] (равны, если [math]\displaystyle{ f }[/math] инъективны[13]) |
[math]\displaystyle{ f^{-1}(B_1 \cap B_2) = f^{-1}(B_1) \cap f^{-1}(B_2) }[/math] |
| [math]\displaystyle{ f(A_1 \setminus A_2) \supseteq f(A_1) \setminus f(A_2) }[/math][11] (равны, если [math]\displaystyle{ f }[/math] инъективна[13]) |
[math]\displaystyle{ f^{-1}(B_1 \setminus B_2) = f^{-1}(B_1) \setminus f^{-1}(B_2) }[/math][11] |
| [math]\displaystyle{ f(A_1 \triangle A_2) \supseteq f(A_1) \triangle f(A_2) }[/math] (равны , если [math]\displaystyle{ f }[/math] инъективна) |
[math]\displaystyle{ f^{-1}(B_1 \triangle B_2) = f^{-1}(B_1) \triangle f^{-1}(B_2) }[/math] |
Результаты для образов и прообразов (булевой) алгебры пересечений и объединений работает для любой коллекции подмножеств, не только для пар подмножеств:
- [math]\displaystyle{ f\left(\bigcup_{s\in S}A_s\right) = \bigcup_{s\in S} f(A_s) }[/math]
- [math]\displaystyle{ f\left(\bigcap_{s\in S}A_s\right) \subseteq \bigcap_{s\in S} f(A_s) }[/math]
- [math]\displaystyle{ f^{-1}\left(\bigcup_{s\in S}B_s\right) = \bigcup_{s\in S} f^{-1}(B_s) }[/math]
- [math]\displaystyle{ f^{-1}\left(\bigcap_{s\in S}B_s\right) = \bigcap_{s\in S} f^{-1}(B_s) }[/math]
(Здесь [math]\displaystyle{ S }[/math] может быть бесконечным множеством, даже несчётным.)
Что касается описанной выше алгебры подмножеств, обратная отображающая функция — это гомоморфизм решётки, в то время как отображающая функция — это лишь гомоморфизм полурешёток (т.е., она не всегда сохраняет пересечения).
См. также
Примечания
- ↑ Compendium of Mathematical Symbols (англ.) ?. Math Vault (1 марта 2020). Дата обращения: 28 августа 2020. Архивировано 6 декабря 2020 года.
- ↑ 5.4: Onto Functions and Images/Preimages of Sets (англ.). Mathematics LibreTexts (5 ноября 2019). Дата обращения: 28 августа 2020. Архивировано 27 октября 2020 года.
- ↑ Weisstein, Eric W. Image (англ.). mathworld.wolfram.com. Дата обращения: 28 августа 2020. Архивировано 19 марта 2020 года.
- ↑ Comprehensive List of Algebra Symbols (англ.) ?. Math Vault (25 марта 2020). Дата обращения: 28 августа 2020. Архивировано 1 апреля 2020 года.
- ↑ Dolecki, Mynard, 2016, с. 4-5.
- ↑ Blyth, 2005, p. 5.
- ↑ Rubin, 1967.
- ↑ M. Randall Holmes: Inhomogeneity of the urelements in the usual models of NFU Архивная копия от 7 февраля 2018 на Wayback Machine, December 29, 2005, on: Semantic Scholar, p. 2
- ↑ 9,0 9,1 9,2 Halmos, 1960, с. 39.
- ↑ 10,0 10,1 Munkres, 2000, с. 19.
- ↑ 11,0 11,1 11,2 11,3 11,4 11,5 11,6 11,7 Lee, 2011, с. 388.
- ↑ 12,0 12,1 Kelley, 1985, p. [[1] в «Книгах Google» 85]
- ↑ 13,0 13,1 Munkres, 2000, с. 21.
Литература
- John M. Lee. Introduction to topological manifolds. — 2nd. — New York, Dordrecht, Heidelberg, London: Springer, 2011. — Т. 202. — (Graduate Texts in Mathematics). — ISBN 978-1-4419-7939-1.
- Jean E. Rubin. Set Theory for the Mathematician. — Holden-Day, 1967. — С. xix.
- Michael Artin. Algebra. — Prentice Hall, 1991. — ISBN 81-203-0871-9.
- T.S. Blyth. Lattices and Ordered Algebraic Structures. — Springer, 2005. — ISBN 1-85233-905-5.
- Szymon Dolecki, Frederic Mynard. Convergence Foundations Of Topology. — New Jersey: World Scientific Publishing Company, 2016. — ISBN 978-981-4571-53-4.
- Paul R. Halmos. Naive set theory. — van Nostrand Company, 1960. — (The University Series in Undergraduate Mathematics).
- John L. Kelley. General Topology. — 2. — Birkhäuser, 1985. — Т. 27. — (Graduate Texts in Mathematics). — ISBN 978-0-387-90125-1.
- James R. Munkres. Topology. — Second ed.. — Upper Saddle River, NJ: Prentice Hall, Inc., 2000. — ISBN 978-0-13-181629-9.
Для улучшения этой статьи желательно: |