Матрица масс

В аналитической механике матрица масс представляет собой симметричную матрицу M, которая выражает связь между производной по времени [math]\displaystyle{ \dot q }[/math] вектора обобщённых координат q системы и кинетической энергией T этой системы по уравнению

[math]\displaystyle{ T = \frac{1}{2} \mathbf{\dot q}^\textsf{T} \mathbf{M} \mathbf{\dot q} }[/math]

где [math]\displaystyle{ \mathbf{\dot q}^\textsf{T} }[/math] обозначает транспонирование вектора [math]\displaystyle{ \mathbf{\dot q} }[/math]^[1]. Это уравнение аналогично формуле для кинетической энергии частицы с массой [math]\displaystyle{ m }[/math] и скоростью v, а именно

[math]\displaystyle{ T = \frac{1}{2} m|\mathbf{v}|^2 = \frac{1}{2} \mathbf{v} \cdot m\mathbf{v} }[/math]

и может быть получено из неё, выражая положение каждой частицы системы через q.

В общем случае матрица масс М зависит от состояния q и поэтому изменяется со временем.

Лагранжева механика даёт обыкновенное дифференциальное уравнение (фактически, система связанных дифференциальных уравнений), которое описывает эволюцию системы в терминах произвольного вектора обобщённых координат, который полностью определяет положение каждой частицы в системе. Приведённая выше формула кинетической энергии является одним из членов этого уравнения, которое представляет общую кинетическую энергию всех частиц.

Примеры

Например, рассмотрим систему, состоящую из двух точечных масс, ограниченных прямой линией. Состояние этих систем может быть описано вектором q двух обобщённых координат, а именно положениями двух частиц вдоль линии.

[math]\displaystyle{ q = \begin{bmatrix} x_1 & x_2 \end{bmatrix}^\textsf{T} }[/math] ,

Предположим, что частицы имеют массы m₁, m₂, кинетическая энергия системы

[math]\displaystyle{ T = \sum_{i=1}^{2} \frac{1}{2} m_i \dot {x_i}^2 }[/math]

Эта формула также может быть записана как

[math]\displaystyle{ T = \frac{1}{2} \dot q^\textsf{T} M \dot q }[/math]

где

[math]\displaystyle{ M = \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix} }[/math]

Система N тел

В более общем случае рассмотрим систему из N частиц, помеченных индексами i = 1, 2,…, N, где положение частицы с номером i определяется n_i свободными декартовыми координатами (где n_i равно 1, 2 или 3). Пусть q будет вектором столбца, содержащим все эти координаты. Матрица масс M представляет собой диагональную блочную матрицу, где в каждом блоке диагональные элементы представляют собой массу соответствующей частицы:^[2]

[math]\displaystyle{ M = \operatorname{diag}\left[ m_1 I_{n_1},\, m_2 I_{n_2},\, \ldots,\, m_N I_{n_N} \right] }[/math]

где I_{n i} — это единичная матрица n_i × n_i, или более полно:

[math]\displaystyle{ M = \begin{bmatrix} m_1 & \cdots & 0 & 0 & \cdots & 0 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \ddots &\vdots & \ddots & \vdots \\ 0 & \cdots & m_1 & 0 & \cdots & 0 & \cdots & 0 & \cdots & 0 \\ 0 & \cdots & 0 & m_2 & \cdots & 0 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \ddots &\vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & m_2 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & 0 & \cdots & m_N & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & 0 & \cdots & 0 & \cdots & m_N\\ \end{bmatrix} }[/math]

Вращающаяся гантель

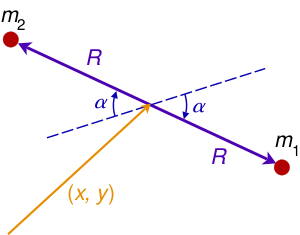
В качестве менее тривиального примера рассмотрим два точечных объекта с массами m₁, m₂, прикреплённых к концам жесткого безмассового стержня длиной 2R, причём узел может свободно вращаться и скользить по фиксированной плоскости. Состояние системы можно описать обобщённым координатным вектором

[math]\displaystyle{ q = \begin{bmatrix} x & y & \alpha \end{bmatrix} }[/math]

где х, у — декартовы координаты средней точки стержня и α представляет собой угол стержня от некоторого произвольного опорного направления. Положения и скорости двух частиц

[math]\displaystyle{ \begin{align} x_1 &= (x, y) + R(\cos\alpha, \sin\alpha) & v_1 &= \left(\dot x, \dot y\right) + R\dot \alpha(-\sin\alpha, \cos\alpha) \\ x_2 &= (x, y) - R(\cos\alpha, \sin\alpha) & v_2 &= \left(\dot x, \dot y\right) - R\dot \alpha(-\sin\alpha, \cos\alpha) \end{align} }[/math]

и их общая кинетическая энергия

[math]\displaystyle{ 2T = m\dot x^2 + m\dot y^2 + mR^2\dot\alpha^2 - 2Rd\sin(\alpha) \dot x \dot\alpha + 2Rd\cos(\alpha) \dot y \dot\alpha }[/math]

где [math]\displaystyle{ m = m_1 + m_2 }[/math] и [math]\displaystyle{ d = m_1 - m_2 }[/math]. Эта формула может быть записана в виде матрицы

[math]\displaystyle{ T = \frac{1}{2} \dot q^\textsf{T} M \dot q }[/math]

где

[math]\displaystyle{ M = \begin{bmatrix} m & 0 & -Rd\sin\alpha \\ 0 & m & Rd\cos\alpha \\ -Rd\sin\alpha & Rd\cos\alpha & R^2 m \end{bmatrix} }[/math]

Обратите внимание, что матрица зависит от текущего угла α стержня.

Механика сплошных сред

Для дискретных приближений механики сплошных сред, как в методе конечных элементов, может быть несколько способов построения матрицы масс, в зависимости от требуемой производительности вычислений и точности. Например, метод с сосредоточенными массами, в котором деформация каждого элемента игнорируется, создаёт диагональную матрицу масс и устраняет необходимость интегрировать массу по деформированному элементу.

См. также

Ссылки

↑ Mathematical methods for physics and engineering, K.F. Riley, M.P. Hobson, S.J. Bence, Cambridge University Press, 2010, ISBN 978-0-521-86153-3
↑ Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978 0 521 57572 0

[Riley-1] Mathematical methods for physics and engineering, K.F. Riley, M.P. Hobson, S.J. Bence, Cambridge University Press, 2010, ISBN 978-0-521-86153-3

[Hand-2] Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, ISBN 978 0 521 57572 0

[1]

[2]