Коэффициент передачи
Коэффицие́нт переда́чи (также коэффициент преобразова́ния, крутизна преобразова́ния) — отношение приращения некоторой физической величины на выходе некоторой системы [math]\displaystyle{ \Delta A_o }[/math] к вызвавшему это приращение, изменению подаваемой на вход велечины данной системы [math]\displaystyle{ \Delta A_i }[/math]:
[math]\displaystyle{ K = \Delta A_o / \Delta A_i. }[/math]
Величину на входе системы часто называют возмущающим воздействием или просто возмущением, а выходную величину — откликом системы.
В общем случае размерности возмущения и отклика не совпадают, например, звуковое давление, развиваемое электродинамическим громкоговорителем и подводимая к нему электрическая мощность, или ЭДС термопары и температура, в этом случае отношение выходной величины к входной часто называют коэффициентом преобразования или крутизной преобразования, при этом коэффициент передачи размерный в приведённых примерах — Па/Вт или В/К.
Если входная и выходная величины имеют одинаковую размерность, то коэффициент передачи — безразмерная величина и его обычно называют коэффициентом усиления. При этом если выходная величина больше по модулю входной величины, то коэффициент усиления больше 1. Если коэффициент усиления меньше 1 то часто используют обратную ему величину [math]\displaystyle{ K_r = 1/K }[/math] называемую коэффициентом ослабления или коэффициентом затухания, или просто затуханием.
В линейных системах коэффициент передачи не зависит от величины возмущения, то есть является постоянной величиной, и связь между откликом и воздействием выражается формулой:
- [math]\displaystyle{ A_o = K A_i. }[/math]
В нелинейных системах связь между откликом и возмущением является некоторой нелинейной функцией, при этом вводят понятие дифференциального коэффициента передачи — производной отклика по возмущению [math]\displaystyle{ K_d = d A_o / d A_i, }[/math] этот коэффициент зависит от величины возмущения. При этом при корректном указании численного значения коэффициента передачи нужно указывать величину возмущения или величину отклика.
Обычно коэффициент передачи не зависит от предыстории системы, но в некоторых системах текущий коэффициент передачи зависит от предыдущий воздействий, например, в электрических цепях с катушками индуктивности с ферромагнитными сердечниками или в цепях с электрохимическими элементами[1]
Логарифмический коэффициент передачи
Безразмерный коэффициент передачи часто численно выражают в виде логарифма по некоторому оговорённому основанию [math]\displaystyle{ a }[/math]:
- [math]\displaystyle{ K_L = \log_a(K) = \log_a(\Delta A_o / \Delta A_i). }[/math]
Для коэффициентов передачи, имеющих размерность, логарифмический коэффициент передачи не имеет смысла, так как будет зависеть от системы выбранных единиц, в отличие от безразмерных коэффициентов передачи инвариантных относительно выбранной системы единиц. Для размерных коэффициентов передачи имеют смысл только логарифмы их отношений, например, на двух разных частотах или при двух разных условиях.
Применение логарифмического коэффициента передачи обусловлено во-первых тем, что при последовательном соединении нескольких систем (звеньев, цепей) с коэффициентами передачи [math]\displaystyle{ K_1 \dots K_i }[/math] результирующий коэффициент передачи равен произведению коэффициентов передачи всех систем:
- [math]\displaystyle{ K = \prod_{i} K_i }[/math]
При замене на логарифмы коэффициентов передачи результирующий логарифмический коэффициент передачи [math]\displaystyle{ K_L }[/math] будет равен сумме логарифмических коэффициентов передачи [math]\displaystyle{ K_{Li} }[/math] в соответствии со свойствами логарифмической функции:
- [math]\displaystyle{ K_L = \log_a(K) = \log_a \prod_{i} K_i = \sum_{i} \log_a (K_i) = \sum_{i} K_{Li}, }[/math]
то есть, перемножение чисел заменяется их сложением, что на практике при расчётах удобнее.
И, во-вторых, коэффициент передачи может изменяться на много порядков, например, при изменении частоты гармонического возбуждающего воздействия и на графиках выражение коэффициентов передачи в виде логарифмов получается нагляднее.
В качестве основания логарифма практически используются три числа, это логарифмы по основанию числа Эйлера [math]\displaystyle{ e }[/math] — натуральные логарифмы, в этом случае единица логарифмического коэффициента передачи называется непер (Нп) — по имени шотландского математика Джона Непера, впервые опубликовавшего таблицы логарифмов. Изменение логарифмического коэффициента передачи на 1 непер соответствует изменению величины в [math]\displaystyle{ e }[/math] раз, ~2,72. Если в качестве основания логарифма использовано число 10 — десятичные логарифмы, то единицу измерения логарифмического коэффициента передачи называют бел (B — международное, Б — русское) названную в честь американского учёного Александра Белла. Изменение величины на 1 Бел соответствует изменению отношения величин в 10 раз. Практически чаще используется дольная единица — децибел, равная 0,1 бела (dB — международное, дБ — русское). Сейчас единица непер практически вытеснена децибелами, но иногда используется и до сих пор, в основном в литературе по телефонной связи. Очень редко используются логарифмы по основанию 2, в основном для выражения отношения частот, также входит в выражение для периода полураспада соответствующая логарифмическая единица называется октава, 1 октава соответствует изменению отношения величин в 2 раза.
Энергетические и силовые логарифмические коэффициенты передачи
Энергетические величины [math]\displaystyle{ P }[/math] (мощность, энергия, плотности энергии, интенсивность звука, световой поток и т. п.) пропорциональны квадрату силовых величин [math]\displaystyle{ A }[/math] характеризующих данное явление, таких как электрическое напряжение, электрический ток, звуковое давление, амплитуда электромагнитного поля в световой волне и др. То есть:
- [math]\displaystyle{ P \sim A^2, }[/math]
- [math]\displaystyle{ \frac {P_o} {P_i} = \frac {A_o^2} {A_i^2}. }[/math]
Соответственно, логарифмические коэффициенты передачи:
- [math]\displaystyle{ \log_a \frac {P_o} {P_i} = \log_a \frac {A_o^2} {A_i^2} = 2 \log_a \frac {A_o} {A_i}. }[/math]
Поэтому логарифмические коэффициенты передачи для энергетических величин в 2 раза больше логарифмических коэффициентов передачи для силовых величин.
Пример. Электрическая мощность на сопротивлении нагрузки [math]\displaystyle{ R }[/math] прямо пропорциональна квадрату напряжения или тока.
- [math]\displaystyle{ P = RI^2 = U^2/R; }[/math]
- [math]\displaystyle{ \log_{10} \frac {P_o} {P_i} = \lg \frac {P_o} {P_i} = \lg \frac {U_o^2} {U_i^2} = \lg \frac {I_o^2} {I_i^2} = 2 \lg \frac {U_o} {U_i}\ (B) = 2 \lg \frac {I_o} {I_i}\ (B) = 20 \lg \frac {U_o} {U_i}\ (dB) = 20 \lg \frac {I_o} {I_i}\ (dB). }[/math]
Соотношения между силовыми и энергетическими логарифмическими коэффициентами передачи выраженные в белах, децибелах и неперах приведены в таблице.
| Единица | Обозначение | Изменение энергетической величины в … раз |
Изменение силовой величины в … раз |
Пересчёт в … | |||
|---|---|---|---|---|---|---|---|
| дБ | Б | Нп | |||||
| децибел | дБ, dB | [math]\displaystyle{ \sqrt[10]{10} }[/math] ≈ 1,259 | [math]\displaystyle{ \sqrt[20]{10} }[/math] ≈ 1,122 | 1 | 0,1 | ≈0,1151 | |
| бел | Б, B | 10 | [math]\displaystyle{ \sqrt{10} }[/math] ≈ 3,162 | 10 | 1 | ≈1,151 | |
| непер | Нп, Np | e2 ≈ 7,389 | e ≈ 2,718 | ≈8,686 | ≈0,8686 | 1 | |
Если коэффициент передачи больше 1, то логарифмический коэффициент передачи положителен, отрицателен при коэффициенте передачи меньше 1 и равен нулю, если коэффициент передачи равен 1.
Также в виде логарифмического коэффициента передачи обычно указывается затухание (ослабление) сигнала в электрических и оптоволоконных линиях передачи, часто в виде удельного ослабления на единицу длины линии, например, в дБ/км, при этом знак минус у логарифмического коэффициента передачи, как правило, не указывается, а подразумевается.
Комплексный коэффициент передачи и модуль коэффициента передачи
Большинство изучаемых систем нелинейны, то есть для них не выполняется принцип суперпозиции. Практически при анализе многие системы поддаются линеаризации — они ведут себя как приближённо линейные для малых изменений возмущающих входных воздействий. Для линейных и линеаризованных систем вводят понятие комплексного коэффициента передачи.
Если на вход линейной или приближённо линейной системы подать гармоническое воздействие [math]\displaystyle{ X }[/math] с амплитудой [math]\displaystyle{ A_i }[/math] и угловой частотой [math]\displaystyle{ \omega }[/math], то на выходе в установившемся режиме тоже будет гармонический отклик [math]\displaystyle{ Y }[/math] с амплитудой [math]\displaystyle{ A_o }[/math] и фазовым сдвигом [math]\displaystyle{ \varphi }[/math] относительно входного воздействия и с той же частотой:
- [math]\displaystyle{ X = A_i \sin(\omega t);\ }[/math] [math]\displaystyle{ Y = A_o \sin(\omega t + \varphi). }[/math]
Гармонические входное возмущение и выходной отклик можно записать в виде комплексных амплитуд, буквой [math]\displaystyle{ j }[/math] обозначена мнимая единица:
- [math]\displaystyle{ X(j \omega t) = A_i e^{j\omega t};\ }[/math] [math]\displaystyle{ Y(j \omega t) = A_o e^{j(\omega t + \varphi)}. }[/math]
По определению коэффициент передачи равен отношению выходного и входного сигналов, в теории автоматического регулирования, теории электрических цепей комплексный коэффициент передачи обычно обозначают как [math]\displaystyle{ H(j\omega) }[/math], подчёркивая тем самым, что коэффициент передачи комплексное число, притом, в общем случае, зависящее от частоты возбуждающего гармонического воздействия [math]\displaystyle{ \omega }[/math]:
- [math]\displaystyle{ H(j\omega) = \frac {Y[j (\omega t + \varphi)]} {X(j \omega t)} = \frac {A_o e^{j(\omega t + \varphi)}} {A_i e^{j\omega t}} = \frac {A_o} {A_i} e^{j \varphi} }[/math]
В этом выражении отношение [math]\displaystyle{ \frac {A_o} {A_i} }[/math] называют модулем коэффициента передачи, а [math]\displaystyle{ e^{j \varphi} }[/math] — множителем фазового сдвига коэффициента передачи или «поворачивающим множителем».
Или в других обозначениях, если записать комплексный коэффициент передачи в нормализованном виде комплексного числа [math]\displaystyle{ H(j\omega) = a + j b, }[/math] где [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] действительная и мнимая части комплексного числа соответственно, то модуль коэффициента передачи будет равен [math]\displaystyle{ \frac {A_o} {A_i} = \sqrt {a^2 + b^2}, }[/math] а аргумент [math]\displaystyle{ \varphi = \operatorname{arctg} \left( \frac {b} {a} \right). }[/math]
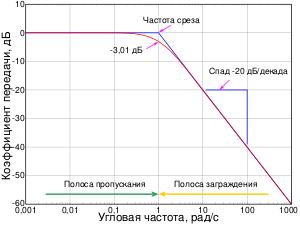
Зависимость комплексного коэффициента передачи линейной системы от частоты возмущения графически можно изобразить в виде амплитудно-фазовой частотной характеристики, где на одном из графиков строится зависимость модуля коэффициента передачи от частоты, а на другом графике — зависимость фазового сдвига от частоты. Обычно для наглядности на оси частот и на оси модуля коэффициента передачи применяют логарифмические координаты, в этом случае такой график называют логарифмической амплитудно-фазовой частотной характеристикой, ось модуля коэффициента передачи обычно оцифровывается в децибелах.
Также комплексный коэффициент передачи графически может изображаться в виде годографа на комплексной плоскости — траектории конца вектора векторного представления комплексного коэффициента передачи при изменении частоты, на этой траектории в виде засечек указывается частота. Графическое представление удобно при анализе устойчивости систем автоматического регулирования, в частности, если годограф коэффициента передачи системы с разомкнутой обратной связью не охватывает точку комплексной плоскости −1, то такая системы при замыкании контура обратной связи будет устойчива.
Другие виды коэффициента передачи
В общем случае отношение выходного сигнала к вызвавшему его входному сигналу любой системы можно назвать коэффициентом передачи. В зависимости от конкретной системы коэффициент передачи может называться по-разному. Например, отношение приращения тока через активный электронный прибор (например, электровакуумный триод, транзистор) в вызвавшему это приращение изменению напряжения на управляющем электроде прибора называют крутизной передаточной характеристики, имеющей размерность электрической проводимости. В измерительных стрелочных приборах отношение отклонения стрелки к вызвавшему это отклонение изменению измеряемой величины называют чувствительностью прибора или ценой деления шкалы.
Применение понятия
В основном термин «коэффициент передачи» используется в электротехнике, электронике, оптике, акустике. Например, коэффициент усиления усилителей, коэффициент затухания сигнала в линиях передачи, ослабление электромагнитного излучения в поглощающих средах, или наоборот, усиление света в активных средах лазеров, в описании поглощения и отражения звуковых волн и поглощении механических вибраций, и т. п.
Методы измерения коэффициента передачи
- Прямое измерение — производится прямым измерением амплитуды сигнала на входе и выходе системы с последующим вычислением. Существуют специализированные оптические и электрические приборы для выполнения такого измерения.
- Измерение методом сравнения — производится с помощью аттенюатора, являющегося мерой ослабления. Например, с помощью аттенюатора ослабляют выходной сигнал усилителя до достижения равенства с входным сигналом, сравнение сигналов производится каким либо компаратором. По степени ослабления калиброванного аттенюатора определяют коэффициент усиления усилителя.
- Для измерения комплексных коэффициентов передачи применяются измерители импеданса и комплексных коэффициентов передачи, или, на сверхвысоких частотах, измерители комплексных коэффициентов и измерители коэффициента стоячей волны.
Примечания
- ↑ Боровков В. С., Графов Б. М. и др. Электрохимические преобразователи первичной информации. М. Машиностроение. 1969. 196 с., ил.
См. также
- Ослабление электромагнитного сигнала
- Усилитель
- Лазерные материалы
- Волоконно-оптический усилитель
- Четырёхполюсник
Литература
- Хлытчиев С. М. Основы автоматики и автоматизации производственных процессов. — 1985.
- Словарь радиолюбителя — Л.: Энергия, 1979.
- Гусев В. Г. Электроника. — 1991.
Ссылки
- Синтез корреляционных алгоритмов идентификации в частотной области.
- Вывод комплексного коэффициента передачи системы каскадно-соединённых взаимодействующих четырёхполюсников.
- О методах описания линейных систем.
- Динамика линейных систем автоматического управления.
Для улучшения этой статьи желательно: |