Графический метод решения задачи линейного программирования

Графический метод решения задачи линейного программирования основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.

Описание метода

Пример графического решения задачи линейного программирования с 6 условиями. Cтроим на плоскости область допустимых решений. У нас 6 неравенств. Неравенства превращаем в равенства, получаем прямые (оси координат задаются неполными уравнениями прямой Ax = 0 определяет ось Oy и By = 0 определяет ось Ox). Проводим прямые. Каждя прямая делить плоскость на две полуплоскости. Каждый раз выбираем одну. Берем точку, если неравенство истинно значит выбираем эту полуплоскость. Если ложно, выбираем противоположную.

Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные.

Найти минимальное значение функции

[math]\displaystyle{ (1)\quad Z = c_1x_1 + c_2x_2 }[/math]

при ограничениях вида

[math]\displaystyle{ (2)\quad \left\{ \begin{matrix} a_{11}x_1 + a_{12}x_2 \leqslant b_1 \\ a_{21}x_1 + a_{22}x_2 \leqslant b_2 \\ \ldots \\ a_{n1}x_1 + a_{n2}x_2 \leqslant b_n \end{matrix} \right . }[/math]

и

[math]\displaystyle{ (3)\quad \left\{ \begin{matrix} x_1 \geqslant 0\\ x_2 \geqslant 0\\ \end{matrix} \right . }[/math]

Допустим, что система (2) при условии (3) совместна. Каждое из неравенств из систем (2) и (3) определяет полуплоскость с граничными прямыми: [math]\displaystyle{ a_{i1}x_1 + a_{i2}x_2 = b_i, (i = 1, 2,\ldots, n); x_1=0; x_2=0 }[/math].

Линейная функция (1) при фиксированных значениях [math]\displaystyle{ Z }[/math] является уравнением прямой линии: [math]\displaystyle{ c_1x_1 + c_2x_2 = const }[/math].

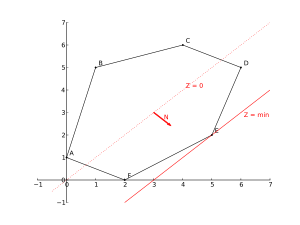
Построим многоугольник решений системы ограничений (2) и график линейной функции (1) при [math]\displaystyle{ Z = 0 }[/math]. Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию:

Найти точку многоугольника решений, в которой прямая [math]\displaystyle{ c_1x_1 + c_2x_2 = const }[/math] опорная и функция [math]\displaystyle{ Z }[/math] при этом достигает минимума.

Значения [math]\displaystyle{ Z = c_1x_1 + c_2x_2 }[/math] уменьшаются в направлении вектора [math]\displaystyle{ N =(-c_1, -c_2) }[/math], поэтому прямую [math]\displaystyle{ Z = 0 }[/math] передвигаем параллельно самой себе в направлении вектора [math]\displaystyle{ N }[/math].

Если многоугольник решений ограничен (см. рисунок), то прямая дважды становится опорной по отношению к многоугольнику решений (в точках [math]\displaystyle{ B }[/math] и [math]\displaystyle{ E }[/math]), причём минимальное значение принимает в точке [math]\displaystyle{ E }[/math]. Координаты точки [math]\displaystyle{ E (x_1, x_2) }[/math] находим, решая систему уравнений прямых [math]\displaystyle{ DE }[/math] и [math]\displaystyle{ EF }[/math].

Если же многоугольник решений представляет собой неограниченную многоугольную область, то возможны два случая.

Случай 1. Прямая [math]\displaystyle{ c_1x_1 + c_2x_2 = const }[/math], передвигаясь в направлении вектора [math]\displaystyle{ N }[/math] или противоположно ему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной к нему. В этом случае линейная функция не ограничена на многоугольнике решений как сверху, так и снизу.

Случай 2. Прямая, передвигаясь, всё же становится опорной относительно многоугольника решений. Тогда в зависимости от вида области линейная функция может быть ограниченной сверху и неограниченной снизу, ограниченной снизу и неограниченной сверху, либо ограниченной как снизу, так и сверху.

Литература

• Кремер Н.Ш. Исследование операций в экономике. — Москва: Юнити, 2000. — С. 55-57. — 408 с.
• Ашманов С.А. Линейное программирование. — Москва: «Наука», 1981. — 304 с.