Релятивистское равноускоренное движение

Релятиви́стское равноуско́ренное движе́ние (или релятивистское равномерно ускоренное движение) — такое движение объекта, при котором его собственное ускорение постоянно. Собственным ускорением называется ускорение объекта в сопутствующей (собственной) системе отсчета, то есть в инерциальной системе отсчёта, в которой текущая мгновенная скорость объекта равна нулю (при этом система отсчёта меняется от точки к точке). Примером релятивистского равноускоренного движения может быть движение тела постоянной массы под действием постоянной (в сопутствующей системе отсчёта) силы. Акселерометр, находящийся на равномерно ускоряющемся теле, не будет менять своих показаний.

Релятивистское равноускоренное движение в важном частном случае одномерного движения называют гиперболическим, поскольку при совпадении направлений векторов скорости и собственного ускорения мировую линию объекта можно представить на диаграмме Минковского, где движение ускоряющейся частицы происходит вдоль оси [math]\displaystyle{ X }[/math], в виде гиперболы. Каждая гипербола определяется через [math]\displaystyle{ x=\pm c^2/\alpha }[/math] и [math]\displaystyle{ \eta=\alpha\tau/c }[/math] (где [math]\displaystyle{ c=1,\quad \alpha=1 }[/math]) в формуле [math]\displaystyle{ cT=x\operatorname{sh}\eta,\quad X=x\operatorname{ch}\eta }[/math]

В отличие от классической механики, физическое тело не может всё время двигаться с неизменным (в фиксированной инерциальной системе отсчёта) ускорением, так как в этом случае его скорость рано или поздно превысит скорость света. Однако собственное ускорение может быть постоянным сколь угодно долго; при этом скорость объекта в фиксированной инерциальной системе отсчёта будет асимптотически приближаться к скорости света, но никогда не превзойдёт её.

В релятивистской механике постоянная сила, действующая на объект, непрерывно изменяет его скорость, оставляя её, тем не менее, меньше скорости света. Простейшим примером релятивистски равноускоренного движения является одномерное движение заряженной частицы в однородном электрическом поле, направленном вдоль скорости.

Для наблюдателя, движущегося с постоянным ускорением в пространстве Минковского, существуют два горизонта событий, так называемые горизонты Риндлера (см. координаты Риндлера).

Зависимость скорости от времени

При воздействии силы [math]\displaystyle{ \textstyle \mathbf{f} }[/math] на объект с постоянной массой [math]\displaystyle{ \textstyle m }[/math] его импульс изменяется следующим образом:

[math]\displaystyle{ \mathbf{f} = \frac{d\mathbf{p}}{dt} = \frac{d}{dt}\frac{m\mathbf{u}}{\sqrt{1-\mathbf{u}^2/c^2}}. }[/math]

Если сила постоянна, то это уравнение легко интегрируется:

[math]\displaystyle{ \frac{\mathbf{u}}{\sqrt{1-\mathbf{u}^2/c^2}}=\mathbf{w}_0+\mathbf{a}\,t, }[/math]

где [math]\displaystyle{ \textstyle \mathbf{a}=\mathbf{f}/m }[/math] — постоянный вектор в направлении силы, а [math]\displaystyle{ \textstyle \mathbf{w}_0 }[/math] — константа интегрирования, выражающаяся через начальную скорость объекта [math]\displaystyle{ \textstyle \mathbf{u}_0 }[/math] в момент времени [math]\displaystyle{ \textstyle t=0 }[/math]:

[math]\displaystyle{ \mathbf{w}_0=\frac{\mathbf{u}_0}{\sqrt{1-\mathbf{u}^2_0/c^2}}. }[/math]

Явное выражение скорости через время имеет вид:

[math]\displaystyle{ \mathbf{u}(t) = \frac{\mathbf{w}_0+\mathbf{a}\,t}{\sqrt{1+(\mathbf{w}_0+\mathbf{a}\,t)^2/c^2}}. }[/math]

Скорость частицы под воздействием постоянной силы стремится к скорости света, но никогда её не превышает. В нерелятивистском пределе малых скоростей зависимость скорости от времени принимает форму

[math]\displaystyle{ \mathbf{u} \approx \mathbf{u}_0+\mathbf{a}\,t }[/math],

отвечающую классическому равноускоренному движению.

Траектория движения

Траектория равноускоренного движения в общем случае зависит от ориентации постоянных векторов [math]\displaystyle{ \textstyle \mathbf{a} }[/math] и [math]\displaystyle{ \textstyle \mathbf{w}_0. }[/math] После интегрирования уравнения [math]\displaystyle{ \textstyle \mathbf{u}(t)=d\mathbf{r}/dt }[/math] получается следующее выражение:

[math]\displaystyle{ \mathbf{r}(t) = \mathbf{r}_0+\frac{\displaystyle\mathbf{a}\,c}{\displaystyle a^2}\, \left( \sqrt{c^2+(\mathbf{w}_0+\mathbf{a}\,t)^2} - \sqrt{c^2+\mathbf{w}_0^2}\right) +\frac{[\mathbf{a}\times[\mathbf{w}_0\times \mathbf{a}]]}{a^2}\cdot\tau_0, }[/math]

где [math]\displaystyle{ \textstyle \mathbf{r}_0 }[/math] — радиус-вектор положения тела в момент времени [math]\displaystyle{ \textstyle t=0, }[/math] а [math]\displaystyle{ \textstyle \tau_0 }[/math] — собственное время объекта:

[math]\displaystyle{ \tau_0 = \frac{c}{a}\cdot \ln\frac{\displaystyle \sqrt{c^2+(\mathbf{w}_0+\mathbf{a}t)^2}+at+(\mathbf{w}_0\mathbf{a})/a}{\displaystyle \sqrt{c^2+\mathbf{w}^2_0}+(\mathbf{w}_0\mathbf{a})/a}. }[/math]

Если собственное ускорение [math]\displaystyle{ \textstyle \mathbf{a} }[/math] и начальная скорость [math]\displaystyle{ \textstyle \mathbf{u}_0 }[/math] параллельны друг другу, то векторное произведение [math]\displaystyle{ \textstyle [\mathbf{a}\times[\mathbf{w}_0\times \mathbf{a}]] }[/math] равно нулю, и выражение для траектории заметно упрощается.

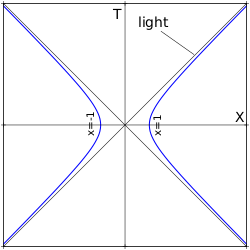
В этом случае, если объект движется вдоль оси x, то его мировая линия на плоскости (x, t) является гиперболой [math]\displaystyle{ x(t) = \mathrm{const} + \sqrt{c^2t^2+c^4/a^2}. }[/math] Поэтому одномерное равноускоренное релятивистское движение иногда называют гиперболическим.

Собственное время [math]\displaystyle{ \textstyle \tau_0 }[/math] равно времени, прошедшему на часах, связанных с объектом, от начального момента [math]\displaystyle{ \textstyle t=0 }[/math] до момента времени [math]\displaystyle{ \textstyle t }[/math] в неподвижной системе отсчёта, относительно которой наблюдается движение. В результате замедления времени всегда [math]\displaystyle{ \textstyle \tau_0\lt t. }[/math]

В нерелятивистском пределе [math]\displaystyle{ \textstyle c\to\infty }[/math] (малые скорости) получается уравнение классического равноускоренного движения:

[math]\displaystyle{ \mathbf{r}(t)\approx \mathbf{r}_0+\mathbf{u}_0\, t+ \frac{\mathbf{a}\,t^2}{2}. }[/math]

Собственное ускорение

Основная статья: Собственное ускорение

Постоянный вектор [math]\displaystyle{ \textstyle \mathbf{a} }[/math] имеет смысл обычного ускорения в мгновенной системе отсчёта, связанной с ускоряющимся телом. Если тело относительно своего предыдущего положения изменяет скорость на [math]\displaystyle{ \textstyle a\,dt', }[/math] где [math]\displaystyle{ \textstyle a = \textrm{const}, }[/math] то в неподвижной системе отсчёта такое движение будет релятивистски равноускоренным. По этой причине параметр [math]\displaystyle{ \textstyle a }[/math] называется собственным ускорением. Приняв такое определение движения, можно получить зависимость скорости от времени, не обращаясь к динамике, оставаясь только в рамках кинематики теории относительности.

Модуль собственного ускорения a в одномерном случае соотносится с модулем 3-ускорения a′ = du/dt , наблюдаемого в фиксированной инерциальной системе отсчёта Λ с координатным временем t, следующим образом:

[math]\displaystyle{ a = a^\prime \gamma^3 = \frac{1}{\left(1-u^2/c^2\right)^{3/2}}\frac{\textrm{d}u}{\textrm{d}t}, }[/math]

где γ — лоренц-фактор объекта, u — его скорость в Λ. Если начальные значения координаты и скорости принять равными нулю, то, интегрируя вышеприведённое уравнение, можно получить зависимости скорости и положения объекта в системе Λ от координатного времени:

[math]\displaystyle{ u(t) = \frac{a t}{\sqrt{1+\left(\frac{a t}{c}\right)^{2}}} =c\operatorname{th}\left(\operatorname{Arsh}\frac{a t}{c}\right); }[/math]

[math]\displaystyle{ x(t) = \frac{c^{2}}{a}\left(\sqrt{1+\left(\frac{a t}{c}\right)^{2}}-1\right) =\frac{c^{2}}{a}\left(\operatorname{ch}\left(\operatorname{Arsh}\frac{a t}{c}\right)-1\right). }[/math]

Зависимость тех же величин от собственного времени объекта:

[math]\displaystyle{ u(\tau) = c\operatorname{th}\frac{a\tau}{c}; }[/math]

[math]\displaystyle{ x(\tau) = \frac{c^{2}}{a}\left(\operatorname{ch}\frac{a\tau}{c}-1\right). }[/math]

Зависимость собственного времени от координатного времени:

[math]\displaystyle{ \tau(t) = \frac{c}{a}\ln\left(\sqrt{1+\left(\frac{a t}{c}\right)^{2}}+\frac{a t}{c}\right) =\frac{c}{a}\operatorname{Arsh}\frac{a t}{c}. }[/math]

Зависимость координатного времени от собственного времени:

[math]\displaystyle{ t(\tau) = \frac{c}{a}\operatorname{sh}\frac{a\tau}{c}. }[/math]

Излучение равномерно ускоренного заряда

Заряд e, движущийся с постоянным собственным ускорением a, излучает электромагнитные волны с мощностью [math]\displaystyle{ P=\frac{2e^2 a^2}{3c^3} }[/math] (в гауссовой системе). При этом радиационное трение отсутствует.

См. также

• Координаты Риндлера
• Быстрота