Двоичная классификация
Двоичная, бинарная или дихотомическая классификация — это задача классификации элементов заданного множества в две группы (предсказание, какой из групп принадлежит каждый элемент множества) на основе правила классификации[англ.]. Контекст, в котором требуется решение, имеет ли объект некоторое качественное свойство[англ.], некоторые специфичные характеристики или некоторую типичную двоичную классификацию, включает:
- Лабораторная диагностика для определения, болеет ли пациент определённой болезнью – классификационным свойством является наличие болезни.
- «Прошёл/не прошёл» метод тестирования[англ.] или технического контроля на заводах, т.е. решение, выполнены или нет спецификации – классификация проходит/не проходит[англ.].
- Информационный поиск, а именно, решение, должна или нет страница или статья попасть в результирующий набор[англ.] поиска – свойством классификации является значимость статьи или полезность для пользователя.
Двоичная классификация является дихотомизацией, применённой для практических нужд. Во многих практических задачах двоичной классификации две группы не симметричны – вместо общей точности важны относительные пропорции типов ошибок. Например, в лабораторных тестах ложно положительный результат[англ.] (выявление болезни, которой на самом деле нет) считается различимым от ложно отрицательного (невыявление болезни, которой на самом деле пациент болеет).
Статистическая двоичная классификация
Статистическая классификация — это задача, изучаемая в обучении машин. Это вид обучения с учителем, метода обучения машин, когда категории предопределены и используются для выбора категории для нового вероятностного наблюдения. Если имеется всего две категории, задача известна как статистическая двоичная классификация.
Некоторые методы, обычно используемые для двоичной классификации:
- Деревья решений
- Случайные леса
- Байесовские сети
- Методы опорных векторов
- Искусственные нейронные сети
- Логистическая регрессия
- Пробит-регрессия
Каждый классификатор ведёт себя наилучшим образом только в выбранной области, основываясь на числе наблюдений, размерности вектора признаков, шуме в данных и многих других факторах. Например, классификаторы на основе случайных лесов работают лучше, чем на основе метода опорных векторов для трёхмерных облаков точек[1][2].
Оценка двоичной классификация
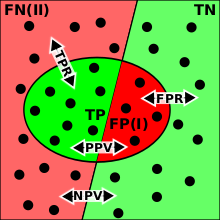
Результаты:
TP=True Positive (правильно положительный);
TN=True Negative (правильно отрицательный);
FP=False Positive (ложно положительный, ошибка типа I);
FN=False Negative (ложно отрицательный, ошибка типа II);
TPR=True Positive Rate (доля правильно положительных);
FPR=False Positive Rate (доля ложно положительных);
PPV=Positive Predictive Value (прогностическая ценность положительного результата);
NPV=Negative Predictive Value (прогностическая ценность ложного результата).
Существует много метрик, которые можно использовать для измерения производительности классификатора или предсказателя. Различные поля имеют различные преимущества для конкретных метрик ввиду различных целей. Например, в медицине часто используются чувствительность и специфичность, в то время как при извлечении информации предпочитают точность и отзыв[англ.]. Важным отличием в метриках заключается в том, является ли она независимой от распространённости (как часто каждая категория встречается в популяции) или зависимой и оба типа полезны, но они имеют очень отличающиеся свойствам.
Если дана классификация множества данных, существует четыре базовые комбинации действительной категории и назначенной категории:
- правильно назначенные положительные классификации[англ.] TP
- правильно назначенные отрицательные классификации[англ.] TN
- ложно назначенные положительные классификации[англ.] FP
- ложно назначенные отрицательные классификации[англ.] FN
Они могут быть расположены в [math]\displaystyle{ 2 \times 2 }[/math] таблице сопряжённости со столбцами, соответствующими действительным значениям – условно положительные (англ. condition positive, CP) или условно отрицательные (англ. condition negative, CN), и строками, соответствующими значениям классификации – результат теста положительный или отрицательный. Существует восемь базовых отношений, которые могут быть вычислены из таблицы, которые распадаются на четыре дополняющие друг друга пары (сумма каждой пары равна 1). Они получаются путём деления каждого из четырёх чисел на сумму по строке или по столбцу, что даёт восемь чисел, о которых можно говорить как о «строке долей верноположительных» или «столбце долей ложноотрицательных», хотя существуют общеупотребимые термины. Существует также две пары отношений столбцов и две пары отношений строк, и можно получить четыре из них путём выбора одного отношения из каждой пары, остальные четыре числа являются их дополнениями.
Столбец долей содержит отношение верноположительных (англ. True Positive Rate, TPR, называемое также чувствительностью или отзывом[англ.], дополнение — доля ложно отрицательных результатов[англ.], англ. False Negative Rate, FNR) и долю верноотрицательных результатов (англ. True Negative Rate, TNR, называемую также специфичностью, (англ. Specificity, SPC, дополнение — доля ложно положительных[англ.], англ. False Positive Rate, FPR). Они пропорциональны популяции с условием (соответственно, без условия) для которой тест верен (или тест ложен) и они не зависят от распространённости.
Строка долей является прогностической ценностью положительного результата[англ.] (англ. Positive Predictive Value, PPV, называемой также точностью, дополнение — доля ложных отклонений[англ.], англ. False Discovery Rate, FDR) и прогностической ценностью отрицательного результата[англ.] (англ. Negative Predictive Value, NPV, дополнение — доля ложных пропусков, англ. False Omission Rate, FOR). Они пропорциональны популяции с заданным верным результатом теста (или ложным результатом) и они зависят от распространённости.
В лабораторных тестах основные используемые отношения — столбец истинных долей – доля верноположительных и доля верноотрицательных результатов – где они известны как чувствительность и специфичность. При извлечении информации главными отношениями являются доля верноположительных (строка и столбец) – прогностическая ценность отрицательного результата и доля верноположительных – где они известны как точность и отзыв[англ.].
Можно взять отношения дополняющих пар отношений, что даёт четыре отношения правдоподобия[англ.] (два значения столбца долей, два значения строки долей). Это, в первую очередь, делается для отношений столбцов, что даёт отношения правдоподобия в лабораторных тестах[англ.]. Взяв отношение в одной из этих групп, получим конечное отношение шансов диагностического теста[англ.] (англ. Diagnostic Odds Ratio, DOR). Это значение можно определить и прямо, как [math]\displaystyle{ (TP \times TN)/(FP \times FN) = (TP/FN)/(FP/TN) }[/math]. Это имеет полезную интерпретацию как отношение шансов и не зависит от распространённости.
Существует несколько других метрик, наиболее простая из которых точность или доля правильных (англ. Fraction Correct, FC), которая измеряет долю всех случаев, которые были правильно классифицированы. Дополнение до 1 этого значения — доля неправильных (англ. Fraction Incorrect, FiC). F-мера[англ.] комбинирует точность и отзыв в одном числе посредством выбора веса, в самом простом случае равному весу как в сбалансированной F-мере (F1 мера[англ.]). Некоторые метрики приходят из коэффициентов регрессии — маркированности и информативности[англ.] и их среднего геометрического, коэффициента корреляции Мэтьюса[англ.]. Другие метрики включают J статистику Юдена[англ.], коэффициент неопределённости[англ.], коэффициент Фи и каппу Коэна.
Преобразование непрерывных значений к бинарным
Тесты, результаты которых являются непрерывными значениями, как, например, большинство значений анализа крови[англ.], могут быть искусственно сделаны двоичными путём определения отсекающего значения[англ.]. Результат теста определяется как положительный или отрицательный в зависимости от итогов сравнения результирующего и отсекающего значений.
Однако такое преобразование приводит к потере информации, поскольку результат двоичной классификации не показывает, насколько выше или ниже значения отсечения. При преобразовании непрерывного значения, которое близко к отсекающему значению, получающаяся в результате положительная[англ.] или отрицательная прогностическая ценность[англ.] в общем случае выше, чем прогностическая ценность[англ.], полученная непосредственно из непрерывного значения. В таких случаях положительный или отрицательный результат теста даёт неприемлемо высокую определённость, в то время как само значение фактически находится в области неопределённости. Например, показатель концентрации хорионического гонадотропина (ХГЧ) в моче имеет непрерывное значение. Тест мочи на беременность с границей отсечения 50 мМЕ/мл при реальной концентрации ХГЧ в значении 52 мМЕ/мл может показывать «положительный результат». С другой стороны, результат теста, далёкий от границы отсечения, обычно имеет положительную или отрицательную прогностическую ценность, меньшую прогностической ценности, полученной от непрерывного значения. Например, значение ХГЧ 200000 мМЕ/мл сообщает об очень высокой степени беременности, но преобразование к двоичным результатам даёт «положительный» результат теста при значении всего лишь 52 мМЕ/мл.
См. также
- Правило классификации[англ.]
- Теория обнаружения сигнала
- Ядерный метод
- Мультиклассовая классификация[англ.]
- Мультизначная классификация[англ.]
- Одноклассовая классификация[англ.]
- Заблуждение прокурора[англ.]
- ROC-кривая
- Пороговая фильтрация[англ.]
- Коэффициент неопределённости[англ.], называемый также адекватностью
- Qualitative property
Примечания
Литература
- Richard Zhang, Avideh Zakhor. Automatic Identification of Window Regions on Indoor Point Clouds Using LiDAR and Cameras // VIP Lab Publications. — 2014.
- Y. Lu, C. Rasmussen. Simplified markov random fields for efficient semantic labeling of 3D point clouds // IROS. — 2012.
- Nello Cristianini, John Shawe-Taylor. An Introduction to Support Vector Machines and other kernel-based learning methods. — Cambridge University Press, 2000. — ISBN 0-521-78019-5.'
- John Shawe-Taylor, Nello Cristianini. Kernel Methods for Pattern Analysis. — Cambridge University Press, 2004. — ISBN 0-521-81397-2.
- Bernhard Scholkopf, A. J. Smola. Learning with Kernels. — Massachusetts: MIT Press, Cambridge, 2002. — ISBN 0-262-19475-9.
Для улучшения этой статьи желательно: |