Размерность Вапника — Червоненкиса
Размерность Вапника — Червоненкиса или VC-размерность — это характеристика семейства алгоритмов для решения задачи классификации с двумя классами, характеризующая сложность или ёмкость этого семейства. Это одно из ключевых понятий в теории Вапника-Червоненкиса о статистическом машинном обучении, названное в честь Владимира Вапника и Алексея Червоненкиса.
Сами Вапник и Червоненкис предпочитают называть эту величину комбинаторной размерностью, так как выяснилось, она была известна алгебраистам еще до открытия их теории машинного обучения.
Определение
Пусть задано множество [math]\displaystyle{ X }[/math] и некоторое семейство индикаторных функций (алгоритмов классификации, решающих правил) [math]\displaystyle{ \mathcal{F} = \{ f(x, \alpha) \} }[/math], где [math]\displaystyle{ x \in X }[/math] — аргумент функций, [math]\displaystyle{ \alpha }[/math] — вектор параметров, задающий функцию. Каждая такая функция [math]\displaystyle{ f(x, \alpha) }[/math] сопоставляет каждому элементу множества [math]\displaystyle{ X }[/math] один из двух заданных классов. VC-размерностью семейства [math]\displaystyle{ \mathcal{F} }[/math] называется наибольшее число [math]\displaystyle{ h }[/math], такое, что существует подмножество из [math]\displaystyle{ h }[/math] элементов множества [math]\displaystyle{ X }[/math], которые функции из [math]\displaystyle{ \mathcal{F} }[/math] могут разбить на два класса всеми возможными способами. Если же такие подмножества существуют для сколь угодно большого [math]\displaystyle{ h }[/math], то VC-размерность полагается равной бесконечности.
VC-размерность можно обобщить и на случай семейства функций [math]\displaystyle{ \{ g(x, \alpha) \} }[/math], принимающих действительные значения. Его VC-размерность определяется как VC-размерность семейства индикаторных функций [math]\displaystyle{ \{ I(g(x, \alpha) \gt \beta) \} }[/math], где [math]\displaystyle{ \beta }[/math] пробегает область значений функций [math]\displaystyle{ g }[/math].[1]
Примеры
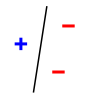
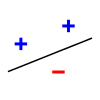
Как пример, рассмотрим задачу о разбиении точек на плоскости на два класса прямой линией — это так называемый линейный классификатор. Множество из любых трёх точек, не лежащих на одной прямой, может быть разделено прямой линией на два класса всеми возможными способами ([math]\displaystyle{ 2^3 = 8 }[/math] способами, на рисунке ниже показаны три из них), но множества из четырёх и более точек — уже нет. Поэтому VC-размерность линейного классификатора на плоскости равна трём.
|
|

|

|
| Примеры разделения трёх точек на два класса |
Разделение невозможно для этих четырёх точек | ||
В общем случае, VC-размерность линейных классификаторов в [math]\displaystyle{ n }[/math]-мерном пространстве равна [math]\displaystyle{ n + 1 }[/math].
См. также
Ссылки
Примечания
- ↑ Hastie, T., Tibshirani R., Friedman J. Chapter 7.9. Vapnik–Chervonenkis Dimension // The Elements of Statistical Learning: Data Mining, Inference, and Prediction. — 2nd ed. — Springer-Verlag, 2009. — 746 p. — ISBN 978-0-387-84857-0..
