Частично упорядоченное множество
Части́чно упоря́доченное мно́жество — математическое понятие, которое формализует интуитивные идеи упорядочения, расположения элементов в определённой последовательности. Неформально, множество частично упорядочено, если указано, какие элементы следуют за какими (какие элементы больше каких). В общем случае может оказаться так, что некоторые пары элементов не связаны отношением «следует за».
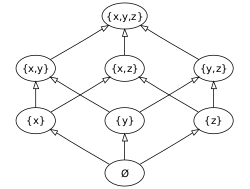
В качестве абстрактного примера можно привести совокупность подмножеств множества из трёх элементов [math]\displaystyle{ \{ x, y, z\} }[/math] (булеан данного множества), упорядоченную по отношению включения.
Определение и примеры
Отношением порядка, или частичным порядком, на множестве [math]\displaystyle{ M }[/math] называется бинарное отношение [math]\displaystyle{ \varphi }[/math] на [math]\displaystyle{ M }[/math] (определяемое некоторым множеством [math]\displaystyle{ R_{\varphi} \subset M \times M }[/math]), удовлетворяющее следующим условиям[1]:
- Рефлексивность: [math]\displaystyle{ \forall a \; (a \varphi a) }[/math]
- Транзитивность: [math]\displaystyle{ \forall a, b, c \; (a \varphi b) \wedge (b \varphi c) \Rightarrow a \varphi c }[/math]
- Антисимметричность: [math]\displaystyle{ \forall a, b \; (a \varphi b) \wedge (b \varphi a) \Rightarrow a = b }[/math]
Множество [math]\displaystyle{ M }[/math], на котором задано отношение частичного порядка, называется частично упорядоченным. Если быть совсем точным[2], то частично упорядоченным множеством называется пара [math]\displaystyle{ \langle M, \varphi \rangle }[/math], где [math]\displaystyle{ M }[/math] — множество, а [math]\displaystyle{ \varphi }[/math] — отношение частичного порядка на [math]\displaystyle{ M }[/math].
Размерность частично упорядоченного множества [math]\displaystyle{ \langle M,\varphi\rangle }[/math] равна максимальной численности совокупности линейных порядков [math]\displaystyle{ \lt _{i} }[/math] ([math]\displaystyle{ i\in I }[/math]). В основе этого определения находится свойство продолжаемости частичного порядка до линейного.
Терминология и обозначения
Отношение частичного порядка обычно обозначают символом [math]\displaystyle{ \leqslant }[/math], по аналогии с отношением «меньше либо равно» на множестве вещественных чисел. При этом, если [math]\displaystyle{ a \leqslant b }[/math], то говорят, что элемент [math]\displaystyle{ a }[/math] не превосходит [math]\displaystyle{ b }[/math], или что [math]\displaystyle{ a }[/math] подчинён [math]\displaystyle{ b }[/math].
Если [math]\displaystyle{ a \leqslant b }[/math] и [math]\displaystyle{ a \neq b }[/math], то пишут [math]\displaystyle{ a \lt b }[/math], и говорят, что [math]\displaystyle{ a }[/math] меньше [math]\displaystyle{ b }[/math], или что [math]\displaystyle{ a }[/math] строго подчинен [math]\displaystyle{ b }[/math].
Иногда, чтобы отличить произвольный порядок на некотором множестве от известного отношения «меньше либо равно» на множестве действительных чисел, вместо [math]\displaystyle{ \leqslant }[/math] и [math]\displaystyle{ \lt }[/math] используют специальные символы [math]\displaystyle{ \preccurlyeq }[/math] и [math]\displaystyle{ \prec }[/math] соответственно.
Строгий и нестрогий порядок
Отношение, удовлетворяющее условиям рефлексивности, транзитивности и антисимметричности, также называют нестрогим, или рефлексивным порядком. Если условие рефлексивности заменить на условие антирефлексивности (тогда свойство антисимметричности заменится на асимметричность):
- [math]\displaystyle{ \forall a \; \neg (a \varphi a) }[/math]
то получим определение строгого, или антирефлексивного порядка.
Если [math]\displaystyle{ \leqslant }[/math] — нестрогий порядок на множестве [math]\displaystyle{ M }[/math], то отношение [math]\displaystyle{ \lt }[/math], определяемое как:
- [math]\displaystyle{ a \lt b \; \overset{\mathrm{def}}{\Longleftrightarrow} \; (a \leqslant b) \wedge (a \neq b) }[/math]
является строгим порядком на [math]\displaystyle{ M }[/math]. Обратно, если [math]\displaystyle{ \lt }[/math] — строгий порядок, то отношение [math]\displaystyle{ \leqslant }[/math], определенное как
- [math]\displaystyle{ a \leqslant b \; \overset{\mathrm{def}}{\Longleftrightarrow} \; (a \lt b) \vee (a = b) }[/math]
является нестрогим порядком.
Поэтому всё равно — задать на множестве нестрогий порядок или строгий порядок. В результате получится одна и та же структура. Разница только в терминологии и обозначениях.
Интервал
Для [math]\displaystyle{ a \leqslant b }[/math] замкнутый интервал [a,b] — это множество элементов x, удовлетворяющих неравенству [math]\displaystyle{ a \leqslant x \leqslant b }[/math] (т.е. [math]\displaystyle{ a \leqslant x }[/math] и [math]\displaystyle{ x \leqslant b }[/math]). Интервал содержит, по меньшей мере, элементы a и b.
Если использовать строгое неравенство "<", получим открытый интервал (a,b), множество элементов x, удовлетворяющих неравенству a < x < b (т.е. a < x и x < b). Открытый интервал может быть пустым, даже если a < b. Например, открытый интервал (1,2) для целых чисел пуст, поскольку нет целых чисел i, таких что 1 < i < 2.
Иногда определение расширяется, позволяя a > b. В этом случае интервал пуст.
Полуоткрытые интервалы [a,b) и (a,b] определяются аналогичным образом.
Частично упорядоченное множество является локально конечным[англ.], если любой интервал конечен. Например, целые числа локально конечны по их естественному упорядочению. Лексикографический порядок на прямом произведении ℕ×ℕ не является локально конечным, поскольку, например, [math]\displaystyle{ (1,2) \leqslant (1,3) \leqslant (1,4) \leqslant (1,5) \leqslant \ldots \leqslant (2,1) }[/math].
Концепцию интервала в частично упорядоченных множествах не следует путать со специфичным классом частичных упорядоченных множеств, известных как интервальные порядки[англ.].
Примеры
- Множество вещественных чисел [math]\displaystyle{ \mathbb{R} }[/math] частично упорядочено по отношению «меньше либо равно» — [math]\displaystyle{ \leqslant }[/math].
- Пусть [math]\displaystyle{ M }[/math] — множество всех вещественнозначных функций, определенных на отрезке [math]\displaystyle{ [a,b] }[/math], то есть функций вида
Введём отношение порядка [math]\displaystyle{ \leqslant }[/math] на [math]\displaystyle{ M }[/math] следующим образом: [math]\displaystyle{ f \leqslant g }[/math], если для всех [math]\displaystyle{ x \in [a,b] }[/math] выполнено неравенство [math]\displaystyle{ f(x) \leqslant g(x) }[/math]. Очевидно, введенное отношение в самом деле является отношением частичного порядка.
- Пусть [math]\displaystyle{ M }[/math] — некоторое множество. Множество [math]\displaystyle{ \mathcal{P}(M) }[/math] всех подмножеств [math]\displaystyle{ M }[/math] (так называемый булеан), частично упорядочено по включению [math]\displaystyle{ M \subseteq N }[/math].
- Множество всех натуральных чисел [math]\displaystyle{ \mathbb{N} }[/math] частично упорядочено по отношению делимости [math]\displaystyle{ m \mid n }[/math].
Связанные определения
Несравнимые элементы
Если [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] — действительные числа, то имеет место только одно из следующих соотношений:
В случае, если [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] — элементы произвольного частично упорядоченного множества, то существует четвёртая логическая возможность: не выполнено ни одно из указанных трех соотношений. В этом случае элементы [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] называются несравнимыми. Например, если [math]\displaystyle{ M }[/math] — множество действительнозначных функций на отрезке [math]\displaystyle{ [0,1] }[/math], то элементы [math]\displaystyle{ f(x) = x }[/math] и [math]\displaystyle{ g(x) = 1-x }[/math] будут несравнимы. Возможность существования несравнимых элементов объясняет смысл термина «частично упорядоченное множество».
Минимальный/максимальный и наименьший/наибольший элементы
Из-за того, что в частично упорядоченном множестве могут быть пары несравнимых элементов, вводятся два различных определения: минимального элемента и наименьшего элемента.
Элемент [math]\displaystyle{ a \in M }[/math] называется минимальным, если не существует элемента [math]\displaystyle{ b \lt a }[/math]. Другими словами, [math]\displaystyle{ a }[/math] — минимальный элемент, если для любого элемента [math]\displaystyle{ b \in M }[/math] либо [math]\displaystyle{ b\gt a }[/math], либо [math]\displaystyle{ b=a }[/math], либо [math]\displaystyle{ b }[/math] и [math]\displaystyle{ a }[/math] несравнимы. Элемент [math]\displaystyle{ a }[/math] называется наименьшим, если для любого элемента [math]\displaystyle{ b \in M }[/math] имеет место неравенство [math]\displaystyle{ b \geqslant a }[/math]. Очевидно, всякий наименьший элемент является также минимальным, но обратное в общем случае неверно: минимальный элемент [math]\displaystyle{ a }[/math] может и не быть наименьшим, если существуют элементы [math]\displaystyle{ b }[/math], не сравнимые с [math]\displaystyle{ a }[/math].
Очевидно, что если в множестве существует наименьший элемент, то он единственен. А вот минимальных элементов может быть несколько. В качестве примера рассмотрим множество [math]\displaystyle{ \mathbb{N}\setminus \{ 1 \} = \{ 2, 3, \ldots \} }[/math] натуральных чисел без единицы, упорядоченное по отношению делимости [math]\displaystyle{ \mid }[/math]. Здесь минимальными элементами будут простые числа, а вот наименьшего элемента не существует.
Аналогично вводятся понятия максимального и наибольшего элементов.
Верхние и нижние грани
Пусть [math]\displaystyle{ A }[/math] — подмножество частично упорядоченного множества [math]\displaystyle{ \langle M, \leqslant\rangle }[/math]. Элемент [math]\displaystyle{ u \in M }[/math] называется верхней гранью [math]\displaystyle{ A }[/math], если любой элемент [math]\displaystyle{ a \in A }[/math] не превосходит [math]\displaystyle{ u }[/math]. Аналогично вводится понятие нижней грани множества [math]\displaystyle{ A }[/math].
Любой элемент, больший, чем некоторая верхняя грань [math]\displaystyle{ A }[/math], также будет верхней гранью [math]\displaystyle{ A }[/math]. А любой элемент, меньший, чем некоторая нижняя грань [math]\displaystyle{ A }[/math], также будет нижней гранью [math]\displaystyle{ A }[/math]. Эти соображения ведут к введению понятий наименьшей верхней грани и наибольшей нижней грани.
Верхнее и нижнее множество
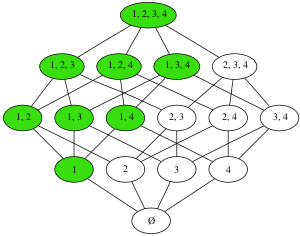
Для элемента [math]\displaystyle{ m }[/math] частично упорядоченного множества [math]\displaystyle{ \langle M, \leqslant\rangle }[/math] верхним множеством называется множество [math]\displaystyle{ M \uparrow m }[/math] всех элементов, которым [math]\displaystyle{ m }[/math] предшествует ([math]\displaystyle{ \{ x \in M \mid m \leqslant x\} }[/math]).
Двойственным образом определяется нижнее множество, как множество всех элементов, предшествующих заданному: [math]\displaystyle{ M \downarrow m \stackrel{\mathrm{def}}{ = } \{ x \in M \mid x \leqslant m\} }[/math].
Условия обрыва цепей
Частично упорядоченное множество [math]\displaystyle{ M }[/math] называется удовлетворяющим условию обрыва строго возрастающих цепей, если не существует бесконечной строго возрастающей последовательности [math]\displaystyle{ (a_i \,\lt \, a_{i+1}) }[/math]. Это условие эквивалентно условию стабилизации нестрого возрастающих цепей: любая нестрого [math]\displaystyle{ (a_i \,\leqslant\, a_{i+1}) }[/math] возрастающая последовательность его элементов стабилизируется. То есть, для любой последовательности вида
- [math]\displaystyle{ a_1 \,\leqslant\, a_2 \,\leqslant\, a_3 \,\leqslant\, \cdots }[/math]
существует натуральное [math]\displaystyle{ n, }[/math] такое что
- [math]\displaystyle{ a_n = a_{n+1} = a_{n+2} = \cdots. }[/math]
Аналогичным образом определяется для убывающих цепей, тогда очевидно, [math]\displaystyle{ M }[/math] удовлетворяет условию обрыва убывающих цепей, тогда и только тогда, когда любая нестрого убывающая последовательность его элементов стабилизируется. Эти понятия часто используются в общей алгебре — см., например, нётерово кольцо, артиново кольцо.
Специальные типы частично упорядоченных множеств
Линейно упорядоченные множества
Пусть [math]\displaystyle{ \langle M, \leqslant\rangle }[/math] — частично упорядоченное множество. Если в [math]\displaystyle{ M }[/math] любые два элемента сравнимы, то множество [math]\displaystyle{ M }[/math] называется линейно упорядоченным. Линейно упорядоченное множество также называют совершенно упорядоченным, или просто, упорядоченным множеством[3]. Таким образом, в линейно упорядоченном множестве для любых двух элементов [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] имеет место одно и только одно из соотношений: либо [math]\displaystyle{ a\lt b }[/math], либо [math]\displaystyle{ a=b }[/math], либо [math]\displaystyle{ b\lt a }[/math].
Также всякое линейно упорядоченное подмножество частично упорядоченного множества называют цепью, то есть цепь в частично упорядоченном множестве [math]\displaystyle{ \langle M, \leqslant \rangle }[/math] — такое его подмножество, в котором любые два элемента сравнимы.
Из приведенных выше примеров частично упорядоченных множеств только множество действительных чисел является линейно упорядоченным. Множество действительнозначных функций на отрезке [math]\displaystyle{ [a, b] }[/math] (при условии [math]\displaystyle{ a\lt b }[/math]), булеан [math]\displaystyle{ \mathcal{P}(M) }[/math] (при [math]\displaystyle{ |M|\geqslant 2 }[/math]), натуральные числа с отношением делимости — не являются линейно упорядоченными.
В линейно упорядоченном множестве понятия наименьшего и минимального, а также наибольшего и максимального, совпадают.
Вполне упорядоченные множества
Линейно упорядоченное множество называется вполне упорядоченным, если каждое его непустое подмножество имеет наименьший элемент[4]. Такой порядок на множестве называется полным порядком, в контексте, где его невозможно спутать с полным порядком в смысле полных частично упорядоченных множеств.
Классический пример вполне упорядоченного множества — множество натуральных чисел [math]\displaystyle{ \mathbb{N} }[/math]. Утверждение о том, что любое непустое подмножество [math]\displaystyle{ \mathbb{N} }[/math] содержит наименьший элемент, равносильно принципу математической индукции. В качестве примера линейно упорядоченного, но не вполне упорядоченного множества можно привести множество неотрицательных чисел, упорядоченное естественным образом [math]\displaystyle{ \mathbb{R}_{+} = \{ x: x \geqslant 0\} }[/math]. Действительно, его подмножество [math]\displaystyle{ \{x: x \gt 1\} }[/math] не имеет наименьшего элемента.
Вполне упорядоченные множества играют исключительно важную роль в общей теории множеств.
Полное частично упорядоченное множество
Полное частично упорядоченное множество — частично упорядоченное множество, у которого есть дно — единственный элемент, который предшествует любому другому элементу и у каждого направленного подмножества которого есть точная верхняя граница[5]. Полные частично упорядоченные множества применяются в λ-исчислении и информатике, в частности, на них вводится топология Скотта, на основе которой строится непротиворечивая модель λ-исчисления и денотационная семантика[англ.]. Специальным случаем полного частично упорядоченного множества является полная решётка — если любое подмножество, не обязательно направленное, имеет точную верхнюю грань, то оно оказывается полной решёткой.
Упорядоченное множество [math]\displaystyle{ M }[/math] тогда и только тогда является полным частично упорядоченным, когда каждая функция [math]\displaystyle{ f \colon M\rightarrow M }[/math], монотонная относительно порядка ([math]\displaystyle{ a \leqslant b \Rightarrow f(a) \leqslant f(b) }[/math]) обладает хотя бы одной неподвижной точкой: [math]\displaystyle{ \exists _{x \in M} f(x)=x }[/math].
Любое множество [math]\displaystyle{ M }[/math] можно превратить в полное частично упорядоченное выделением дна [math]\displaystyle{ \bot }[/math] и определением порядка [math]\displaystyle{ \leqslant }[/math] как [math]\displaystyle{ \bot \leqslant m }[/math] и [math]\displaystyle{ m \leqslant m }[/math] для всех элементов [math]\displaystyle{ m }[/math] множества [math]\displaystyle{ M }[/math].
Теоремы о частично упорядоченных множествах
К числу фундаментальных теорем о частично упорядоченных множествах относятся принцип максимума Хаусдорфа и лемма Куратовского — Цорна. Каждая из этих теорем эквивалентна аксиоме выбора.
В теории категорий
Каждое частично упорядоченное множество (и каждый предпорядок) можно рассматривать как категорию, в которой каждое множество морфизмов [math]\displaystyle{ \mathrm{Hom}(A,B) }[/math] состоит не более чем из одного элемента. Например, эту категорию можно определить так: [math]\displaystyle{ \mathrm{Hom}(A,B)=\{(A,B)\} }[/math], если A ≤ B (и пустое множество в противном случае); правило композиции морфизмов: (y, z)∘(x, y) = (x, z). Каждая категория-предпорядок эквивалентна частично упорядоченному множеству.
Функтор из категории-частично упорядоченного множества (то есть диаграмма, категория индексов которой является частично упорядоченным множеством) — это коммутативная диаграмма.
Примечания
- ↑ Колмогоров, 2004, с. 36.
- ↑ Александров, 1977, с. 78.
- ↑ Колмогоров, 2004, с. 38.
- ↑ Колмогоров, 2004, с. 40.
- ↑ Барендрегт, 1985, с. 23.
Литература
- Александров П. С. Введение в теорию множеств и общую топологию. — М.: Наука, 1977. — 368 с.
- Барендрегт, Хенк. Ламбда-исчисление. Его синтаксис и семантика = The Lambda Calculus. Its syntax and semantics. — М.: Мир, 1985. — 606 с. — 4800 экз.
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — 7-е изд. — М.: Физматлит, 2004. — 572 с. — ISBN 5-9221-0266-4.
- Хаусдорф Ф. Теория множеств. — 4-е изд. — М.: УРСС, 2007. — 304 с. — ISBN 978-5-382-00127-2.
- Гуров С.И. Булевы алгебры, упорядоченные множества, решетки: Определения, свойства, примеры. — 2-е изд. — М.: Либроком, 2013. — 352 с. — ISBN 978-5-397-03899-7.