Знак (математика)

Знак вещественного числа в арифметике позволяет отличить отрицательные числа от положительных; традиционно знак обозначается символом плюса (положительные числа) или минуса (отрицательные) перед записью числа. Если ни плюс, ни минус не указаны, число считается положительным. Ноль как особое число не имеет знака.
Примеры записи чисел: [math]\displaystyle{ +36{,}6;\ {-}273;\ 142. }[/math] Последнее число не имеет знака и поэтому положительно.
Плюс и минус указывают знак для чисел, но не для буквенных переменных или алгебраических выражений. Например, в формулах [math]\displaystyle{ -t;\ a+b;\ -(a^2+b^2) }[/math] символы плюса и минуса задают не знак выражения, перед которым они стоят, а знак арифметической операции, так что знак результата может быть любым, он определяется только после вычисления выражения.
Кроме арифметики, понятие знака используется в других разделах математики, в том числе для нечисловых математических объектов (см. ниже). Понятие знака важно также в тех разделах физики, где физические величины делятся на два класса, условно названные положительными и отрицательными — например, электрические заряды, температура, положительная и отрицательная обратная связь, высота над уровнем моря, разнообразные силы притяжения и отталкивания. В экономике знак позволяет отличать прибыль от убытка, положительный баланс кредитной карты от отрицательного и т. п.
Знак числа
Положительные и отрицательные числа

Вещественное число называется положительным, если оно больше нуля, и отрицательным, если меньше. Положительные числа записываются со знаком плюс или вообще без знака, отрицательные — со знаком минус[1].
Нулю не присвоен никакой знак, то есть [math]\displaystyle{ +0 }[/math] и [math]\displaystyle{ -0 }[/math] — это в арифметике одно и то же число[1]. В теории пределов математического анализа смысл символов [math]\displaystyle{ +0 }[/math] и [math]\displaystyle{ -0 }[/math] может различаться, см. об этом Отрицательный и положительный ноль. В информатике компьютерная кодировка двух нулей (целого типа) также может не совпадать, см. Прямой код.
В связи со сказанным вводятся ещё несколько полезных терминов:
- Число неотрицательно, если оно больше или равно нулю.
- Число неположительно, если оно меньше или равно нулю.
- Положительные числа без нуля и отрицательные числа без нуля иногда (чтобы подчеркнуть, что они ненулевые) называют "'строго положительными" и "строго отрицательными" соответственно.
Та же терминология иногда используется для вещественных функций. Например, функция называется положительной, если все её значения положительны, неотрицательной, если все её значения неотрицательны и т. д. Говорят также, что функция положительна/отрицательна на заданном интервале её определения..
Для комплексных чисел понятия знака числа не существует, потому что для них не определено, как сравнивать числа на больше/меньше.
Обозначения
- Множество положительных действительных чисел обозначается как [math]\displaystyle{ \R_{\gt 0} }[/math].
- Множество неотрицательных действительных чисел обозначается как [math]\displaystyle{ \R_{\geqslant0} }[/math].
- Множество отрицательных действительных чисел обозначается как [math]\displaystyle{ \R_{\lt 0} }[/math].
- Множество неположительных действительных чисел обозначается как [math]\displaystyle{ \R_{\leqslant0} }[/math].
Функция знака sgn(x)
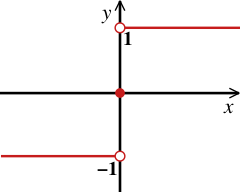
Функция знака [math]\displaystyle{ y=\sgn(x) }[/math] (произносится: сигнум от x) часто бывает полезна как индикатор знака числа. Эта функция определяется следующим образом:
- [math]\displaystyle{ \sgn(x) = \begin{cases} -1 \quad (x \lt 0), \\ ~~\, 0 \quad (x = 0), \\ ~~\, 1 \quad (x \gt 0). \end{cases} }[/math]
Другими словами, функция равна [math]\displaystyle{ 1 }[/math] для положительного аргумента, [math]\displaystyle{ -1 }[/math] для отрицательного и нулю для нулевого аргумента. Функция предусмотрена и в ряде языков программирования.
Пример использования функции см. в статье Квадратный корень#Комплексные числа.
Модуль (абсолютная величина) числа
Если у числа [math]\displaystyle{ x }[/math] отбросить знак, полученное значение называется модулем или абсолютной величиной числа [math]\displaystyle{ x }[/math], оно обозначается [math]\displaystyle{ |x|. }[/math] Примеры: [math]\displaystyle{ |3| = 3;\ |{-3}| = 3. }[/math]
Для любых вещественных чисел [math]\displaystyle{ a,b }[/math] имеют место следующие свойства.
- Формула разложения числа на знак и модуль: [math]\displaystyle{ a = \sgn(a) \cdot |a| }[/math]
- Модуль любого числа всегда неотрицателен, причём [math]\displaystyle{ |a|=0 }[/math] тогда и только тогда, когда [math]\displaystyle{ a=0. }[/math]
- Модули противоположных чисел совпадают: [math]\displaystyle{ |{-a}| = |a|. }[/math]
- [math]\displaystyle{ -|a| \leqslant a \leqslant |a|. }[/math]
- [math]\displaystyle{ |a+b| \leqslant |a|+|b| }[/math] (неравенство треугольника).
Знак у нечисловых объектов
Знак угла

Величина угла на плоскости считается положительной, если она измеряется против часовой стрелки, иначе — отрицательной. Аналогично классифицируются два случая вращения:
- вращение на плоскости — например, вращение на (–90°) происходит по часовой стрелке;
- поворот в пространстве вокруг ориентированной оси, как правило, считается положительным, если выполнено «правило буравчика», иначе он считается отрицательным.
Знак направления
В аналитической геометрии и физике нередко продвижения вдоль заданной прямой или кривой условно делятся на положительные и отрицательные. Такое деление может зависеть от постановки задачи или от выбранной системы координат. Например, при подсчёте длины дуги кривой часто удобно приписать этой длине на одном из двух возможных направлений знак минус.
Знак в вычислительной технике
| старший бит | |||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | 127 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | 126 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | = | 2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | = | −1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | = | −2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | = | −127 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = | −128 |
| Для представления знака целого числа большинство компьютеров используют дополнительный код. | |||||||||
Целое число, хранящееся в памяти компьютера, может быть знаковым или беззнаковым (в последнем случае оно рассматривается как положительное). Знаковые числа используют один из битов как код знака (обычно 0 кодирует положительное число, 1 — отрицательное), у беззнаковых все биты равноправны. Для представления знака и значения целых чисел большинство компьютеров используют дополнительный код, хотя встречается и прямой код.
Вещественные числа хранятся и обрабатываются как числа с плавающей запятой, то есть содержат мантиссу и порядок числа, причём каждая из этих частей снабжена битом своего знака.
Дискретная математика
В комбинаторике определяется знак перестановки — положительный, если перестановка чётная, и отрицательный, если перестановка нечётная. При таком определении выполняется обычное правило знаков для произведения (композиции) перестановок: плюс на плюс и минус на минус дают плюс, плюс на минус и минус на плюс дают минус.
В теории графов рассматриваются ориентированные и знаковые графы[англ.], в которых каждому ребру соответствует направление или знак (положительный или отрицательный).
Физика

Многие физические величины делятся на два класса, условно названные положительными и отрицательными.
Примеры.
- Электрический заряд электрона по исторической традиции называется отрицательным, а протона — положительным.
- Знак температуры зависит от выбранной температурной шкалы. В шкале Кельвина температура всегда неотрицательна, в шкале Цельсия температура выше [math]\displaystyle{ +273^\circ }[/math] Кельвина считается положительной, а ниже — отрицательной.
- В оптике положительной считается оптическая сила линз, собирающих лучи света, и отрицательной, если рассеивающих.
- Высота над уровнем моря.
Другие применения знака
Существует знако-разрядная система счисления[англ.], в ней каждая цифра числа может иметь положительный или отрицательный знак..
В теории меры определено понятие обобщённой меры со знаком («заряда»), которая может иметь положительные или отрицательные значения.
Знак может быть присвоен бесконечно удалённой точке расширенной числовой оси.
См. также
Примечания
- ↑ 1,0 1,1 Справочник по элементарной математике, 1978, с. 111—113.
Литература
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.