Недетерминированный конечный автомат

Недетерминированный конечный автомат (НКА, англ. nondeterministic finite automaton, NFA) — это детерминированный конечный автомат (ДКА, англ. deterministic finite automaton, DFA), который не выполняет следующие условия:

любой его переход единственным образом определяется по текущему состоянию и входному символу
чтение входного символа требуется для каждого изменения состояния.

В частности, любой ДКА является также НКА.

Используя алгоритм конструкции подмножеств^[англ.], любой НКА можно преобразовать в эквивалентный ДКА, то есть ДКА, распознающий тот же самый формальный язык^[1]. Подобно ДКА, НКА распознаёт только регулярные языки.

НКА предложили в 1959 году Михаэль О. Рабин и Дана Скотт^[2], которые показали его эквивалентность ДКА. НКА используется в реализации регулярных выражений — построение Томпсона^[англ.] является алгоритмом для преобразования регулярного выражения в НКА, который может эффективно распознавать шаблон строк. Обратно, алгоритм Клини^[англ.] можно использовать для преобразования НКА в регулярное выражение, размер которого в общем случае экспоненциально зависит от размера автомата.

НКА обобщён многими путями, например: недетерминированным конечным автоматом с ε-переходами, преобразователями с конечным числом состояний, автоматами с магазинной памятью, альтернирующими автоматами, ω-автоматами и вероятностными автоматами. Кроме ДКА известны другие специальные случаи НКА — однозначные конечные автоматы^[англ.] (англ. unambiguous finite automata, UFA) и самопроверочные конечные автоматы^[англ.] (англ. self-verifying finite automata, SVFA).

Неформальное введение

Есть несколько неформальных эквивалентных описаний:

НКА, подобно ДКА, принимает строку входных символов. Для каждого входного символа он переходит в новое состояние, пока не обработает все входные символы. На каждом шаге автомат произвольным образом выбирает один из возможных переходов. Если существует «удачный проход», то есть некоторая последовательность выборов, приводящая к конечному состоянию после полной выборки входной строки, то строка принимается. Если же нет последовательности, которая после обработки всей входной строки^[3] приводит автомат в конечное состояние, то входная строка отвергается^[4]^[5].
Пусть опять НКА принимает строку входных символов, один символ за другим. На каждом шаге, где два или более перехода оказываются допустимыми, автомат «клонирует» себя на нужное число копий, каждая из которых осуществляет различные переходы. Если никакой из переходов не может быть осуществлён, текущая копия является тупиком и «умирает». Если после выборки всех символов из входной строки какая-либо из копий переходит в конечное состояние, входная строка принимается, в противном случае — отвергается^[6]^[7]^[8].

Формальное определение

Для более элементарного введения в формальное определение см. статью «Теория автоматов».

Автоматы

НКА формально представляется как 5-кортеж [math]\displaystyle{ (Q, \Sigma, \Delta, q_0, F) }[/math], состоящий из:

конечного множества состояний [math]\displaystyle{ Q }[/math].
конечного множества входных символов [math]\displaystyle{ \Sigma }[/math].
функции переходов [math]\displaystyle{ \Delta }[/math] : [math]\displaystyle{ Q\times\Sigma \rightarrow P(Q) }[/math].
начального состояния [math]\displaystyle{ q_0 \in Q }[/math].
множества состояний [math]\displaystyle{ F }[/math] распознаваемых как конечные состояния [math]\displaystyle{ F \subseteq Q }[/math].

Здесь [math]\displaystyle{ P(Q) }[/math] означает степень множества [math]\displaystyle{ Q }[/math].

Распознаваемый язык

Если дан НКА [math]\displaystyle{ M = (Q, \Sigma, \Delta, q_0, F) }[/math], он распознаёт язык, который обозначается как [math]\displaystyle{ L(M) }[/math] и определяется как множество всех строк над алфавитом [math]\displaystyle{ \Sigma }[/math], принимаемых автоматом [math]\displaystyle{ M }[/math].

В общих чертах согласно неформальным объяснениям выше, существует несколько эквивалентных формальных определений строки [math]\displaystyle{ w = a_1 a_2 ... a_n }[/math], принимаемых автоматом [math]\displaystyle{ M }[/math]:

[math]\displaystyle{ w }[/math] принимается, если существует последовательность состояний [math]\displaystyle{ r_0, r_1, ..., r_n }[/math] в [math]\displaystyle{ Q }[/math] такая, что
1. [math]\displaystyle{ r_0 = q_0 }[/math]
2. [math]\displaystyle{ r_{i+1} \in \Delta (r_i, a_{i+1}) }[/math], для [math]\displaystyle{ i = 0, \ldots, n-1 }[/math]
3. [math]\displaystyle{ r_n \in F }[/math].

Словами. Первое условие гласит, что машина начинает работу из состояния [math]\displaystyle{ q_0 }[/math]. Второе условие гласит, что для каждого символа строки [math]\displaystyle{ w }[/math] машина переходит из состояния в состояние согласно функции переходов [math]\displaystyle{ \Delta }[/math]. Последнее условие гласит, что машина принимает строку [math]\displaystyle{ w }[/math], если входная строка [math]\displaystyle{ w }[/math] приводит машину к завершению в конечном состоянии. Чтобы строка [math]\displaystyle{ w }[/math] была принята автоматом [math]\displaystyle{ M }[/math], не требуется, чтобы любая последовательность состояний завершается в конечном состоянии, достаточно, чтобы в такое состояние приводила одна последовательность. В противном случае, то есть, если невозможно перейти из [math]\displaystyle{ q_0 }[/math] в состояние из [math]\displaystyle{ F }[/math], следуя [math]\displaystyle{ w }[/math], говорят, что автомат отвергает строку. Множество строк, которые автомат [math]\displaystyle{ M }[/math] принимает, является языком, распознаваемым автоматом [math]\displaystyle{ M }[/math], и этот язык обозначается как [math]\displaystyle{ L(M) }[/math]^[9]^[10].

Альтернативно, [math]\displaystyle{ w }[/math] принимается, если [math]\displaystyle{ \Delta^*(q_0, w) \cap F \not = \emptyset }[/math], где [math]\displaystyle{ \Delta^*: Q \times \Sigma^* \rightarrow P(Q) }[/math] определяется рекурсивно:
1. [math]\displaystyle{ \Delta^*(r, \epsilon) = \{r\} }[/math], где [math]\displaystyle{ \epsilon }[/math] является пустой строкой
2. [math]\displaystyle{ \Delta^*(r, xa)= \bigcup_{r' \in \Delta^*(r, x)} \Delta(r', a) }[/math] для любого [math]\displaystyle{ x \in \Sigma^*, a \in \Sigma }[/math].

Словами, [math]\displaystyle{ \Delta^*(r, x) }[/math] является множеством всех состояний, достижимых из состояния [math]\displaystyle{ r }[/math] при получении строки [math]\displaystyle{ x }[/math]. Строка [math]\displaystyle{ w }[/math] принимается, если некоторое конечное состояние из [math]\displaystyle{ F }[/math] может быть достигнуто из начального состояния [math]\displaystyle{ q_0 }[/math] для входной строки [math]\displaystyle{ w }[/math]^[11]^[12].

Начальное состояние

Определение автомата выше использует одно начальное состояние, что не является обязательным условием. Иногда НКА определяется с множеством начальных состояний. Существует простое построение^[англ.], которое переносит НКА с несколькими начальными состояниями в НКА с одним начальным состоянием.

Пример

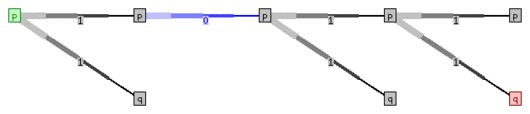Диаграмма состояний автомата M. Он не является детерминированным, поскольку из состояния p чтение 1 может привести в p или в q	Все возможные прогоны автомата M на входной строке «10»
Все возможные прогоны автомата M на входной строке «1011». Метка дуги: входной символ, метка узла: состояние, зелёный: начальное состояние, красный: конечные состояния

Следующий автомат [math]\displaystyle{ M }[/math] с двоичным алфавитом определяет, кончается ли входная строка единицей. Пусть [math]\displaystyle{ M = (\{p, q\}, \{0, 1\}, \Delta, p, \{q\}) }[/math], где функция переходов [math]\displaystyle{ \Delta }[/math] может быть определена следующей таблицей переходов состояний^[англ.] (сравните с верхним рисунком слева):

Вход Состояние	0	1
[math]\displaystyle{ p }[/math]	[math]\displaystyle{ \{p\} }[/math]	[math]\displaystyle{ \{p,q\} }[/math]
[math]\displaystyle{ q }[/math]	[math]\displaystyle{ \emptyset }[/math]	[math]\displaystyle{ \emptyset }[/math]

Поскольку множество [math]\displaystyle{ \Delta(p,1) }[/math] содержит более одного состояния, автомат [math]\displaystyle{ M }[/math] является недетерминированным. Язык автомата [math]\displaystyle{ M }[/math] можно описать как регулярный язык, задаваемый регулярным выражением (0|1)*1.

Все возможные последовательности состояний для входной строки «1011» показаны на нижнем рисунке. Строка принимается автоматом [math]\displaystyle{ M }[/math], поскольку одна из последовательностей состояний удовлетворяет вышеописанному определению. Не имеет значения факт, что остальные последовательности не приводят к успеху. Рисунок можно интерпретировать двумя способами:

В терминах вышеприведённого объяснения «удачного прогона», каждый путь на рисунке означает последовательность выборов [math]\displaystyle{ M }[/math].
Для объяснения в терминах «клонирования» каждый вертикальный столбец показывает все клоны автомата [math]\displaystyle{ M }[/math] в данный момент времени, несколько стрелок, исходящих из узла, означают клонирование, узел без исходящих стрелок означает «смерть» клона.

Возможность чтения одного рисунка двумя способами также показывает эквивалентность двух объяснений выше.

Если рассмотреть первое из формальных определений выше, строка «1011» принимается, поскольку при её чтении [math]\displaystyle{ M }[/math] может пройти последовательность состояний [math]\displaystyle{ \langle r_0,r_1,r_2,r_3,r_4 \rangle = \langle p, p, p, p, q \rangle }[/math], которая удовлетворяет условиям 1-3.
Если рассмотреть второе из формальных определений, проход снизу вверх показывает, что [math]\displaystyle{ \Delta^*(p,\epsilon) = \{ p \} }[/math], следовательно, [math]\displaystyle{ \Delta^*(p,1) = \Delta(p,1) = \{ p,q \} }[/math], а тогда [math]\displaystyle{ \Delta^*(p,10) = \Delta(p,0) \cup \Delta(q,0) = \{ p \} \cup \{\} }[/math], откуда [math]\displaystyle{ \Delta^*(p,101) = \Delta(p,1) = \{ p,q \} }[/math], и, наконец, [math]\displaystyle{ \Delta^*(p,1011) = \Delta(p,1) \cup \Delta(q,1) = \{ p,q \} \cup \{\} }[/math]. Поскольку это множество содержит [math]\displaystyle{ \{ q \} }[/math], строка «1011» принимается.

Для контраста строка «10» отвергается автоматом [math]\displaystyle{ M }[/math] (все возможные последовательности состояний для входной строки для данного входа показаны на верхнем правом рисунке), поскольку не существует пути, достигающего конечного состояния [math]\displaystyle{ q }[/math] после чтения конечного символа 0. Хотя состояние [math]\displaystyle{ q }[/math] может быть достигнуто после получения первого символа «1», это не означает, что входная строка «10» приемлема. Это лишь означает, что была бы приемлема входная строка «1».

Эквивалентность ДКА

Детерминированный конечный автомат (ДКА, англ. Deterministic finite automaton, DFA) можно рассматривать как специальный вид НКА, в котором для любого состояния и букв алфавита функция перехода имеет лишь одно результирующее состояние. Таким образом ясно, что любой формальный язык, который можно распознать с помощью ДКА, можно распознать и с помощью НКА.

В обратную сторону для любого НКА существует ДКА, распознающий тот же самый формальный язык. ДКА может быть построен^[англ.] с помощью конструкции подмножеств^[англ.].

Этот результат показывает, что НКА, несмотря на его большую гибкость, не в состоянии распознать языки, которые нельзя распознать никаким ДКА. Это важно также на практике, чтобы конвертировать более простые по структуре НКА в более эффективные в вычислительном отношении ДКА. Однако, если НКА имеет n состояний, результирующий ДКА может иметь до 2ⁿ состояний, что иногда делает построение непрактичным для больших НКА.

НКА с ε-переходами

Недетерминированный конечный автомат с ε-переходами (НКА-ε) является дальнейшим обобщением уже для НКА. В этом автомате функции переходов разрешается иметь пустую строку ε в качестве входа. Переход без использования входного символа называется ε-переходом. В диаграмме состояний эти переходы обычно помечаются греческой буквой ε. ε-переходы дают удобный способ моделирования систем, текущее состояние которых в точности не известно. Например, если мы моделируем систему, текущее состояние которой не ясно (после обработки некоторой входной строки) и может быть либо q, либо q', мы можем добавить ε-переход между этими двумя состояниями, переводя автомат в оба состояния одновременно.

Формальное определение

НКА-ε формально представляется 5-кортежем, [math]\displaystyle{ (Q, \Sigma, \Delta, q_0, F) }[/math], который состоит из:

конечного множества состояний [math]\displaystyle{ Q }[/math]
конечного множества входных символов, называемого алфавитом [math]\displaystyle{ \Sigma }[/math]
функции переходов [math]\displaystyle{ \Delta : Q \times (\Sigma \cup \{\epsilon\}) \rightarrow P(Q) }[/math]
начального (или стартового) состояния [math]\displaystyle{ q_0 \in Q }[/math]
набора состояний [math]\displaystyle{ F }[/math], считающихся допустимыми (или конечными) состояниями [math]\displaystyle{ F \subseteq Q }[/math].

Здесь [math]\displaystyle{ P(Q) }[/math] означает степень множества [math]\displaystyle{ Q }[/math], а ε означает пустую строку.

ε-Замыкание состояния или множества состояний

Для состояния [math]\displaystyle{ q \in Q }[/math] пусть [math]\displaystyle{ E(q) }[/math] означает множество состояний, достижимых из [math]\displaystyle{ q }[/math] следующими ε-переходами в функции переходов [math]\displaystyle{ \Delta }[/math], а именно, [math]\displaystyle{ p \in E(q) }[/math] если существует последовательность состояний [math]\displaystyle{ q_1,..., q_k }[/math] таких, что:

[math]\displaystyle{ q_1 = q }[/math],
[math]\displaystyle{ q_{i+1} \in \Delta(q_i, \epsilon) }[/math] для любых [math]\displaystyle{ 1 \leqslant i \lt k }[/math]
[math]\displaystyle{ q_k = p }[/math].

Множество [math]\displaystyle{ E(q) }[/math] известно как ε-замыкание состояния [math]\displaystyle{ q }[/math].

ε-замыкание определяется также для множества состояний. ε-замыкание множества состояний, [math]\displaystyle{ P }[/math], НК-автомата определяется как множество состояний, достижимых из элементов множества [math]\displaystyle{ P }[/math] по ε-переходам. Формально, для [math]\displaystyle{ P \subseteq Q E(P) = \cup_{q \in P} E(q) }[/math].

Принимаемые состояния

Пусть [math]\displaystyle{ w = a_1 a_2 ... a_n }[/math] будет строкой над алфавитом [math]\displaystyle{ \Sigma }[/math]. Автомат [math]\displaystyle{ M }[/math] принимает строку [math]\displaystyle{ w }[/math], если существует последовательность состояний [math]\displaystyle{ r_0, r_1, ..., r_n }[/math] в [math]\displaystyle{ Q }[/math] со следующими условиями:

[math]\displaystyle{ r_0 \in E(q_0) }[/math]
[math]\displaystyle{ r_{i+1} \in E(r') }[/math], где [math]\displaystyle{ r' \in \Delta(r_i, a_{i+1}) }[/math] для любого [math]\displaystyle{ i=0,...,n-1 }[/math]
[math]\displaystyle{ r_n \in F }[/math].

Словами. Первое условие говорит, что машина начинает с состояния, которое достижимо из состояния [math]\displaystyle{ q_0 }[/math] по ε-переходам. Второе условие говорит, что после чтения [math]\displaystyle{ a_i }[/math] машина выбирает переход [math]\displaystyle{ \Delta }[/math] из [math]\displaystyle{ r_i }[/math] в [math]\displaystyle{ r' }[/math], а затем осуществляет любое число ε-переходов согласно [math]\displaystyle{ \Delta }[/math] для перехода из [math]\displaystyle{ r' }[/math] в [math]\displaystyle{ r_{i+1} }[/math]. Последнее условие говорит, что машина принимает [math]\displaystyle{ w }[/math], если последний входной символ приводит к переходу машины в одно из принимаемых состояний. В противном случае говорят, что автомат отвергает строку. Множество строк, которые [math]\displaystyle{ M }[/math] принимает, является языком, который распознаёт автомат [math]\displaystyle{ M }[/math], и этот язык обозначается как [math]\displaystyle{ L(M) }[/math].

Пример

Пусть [math]\displaystyle{ M }[/math] будет НКА-ε с двоичным алфавитом, который определяет, если входная строка содержит чётное число нулей или чётное число единиц. Заметим, что 0 случаев является чётным числом.

В формальных обозначениях, пусть [math]\displaystyle{ M = (\{S_0, S_1, S_2, S_3, S_4\}, \{0, 1\}, \Delta, S_0, \{S_1, S_3\}) }[/math], где отношение переходов [math]\displaystyle{ \Delta }[/math] может быть определено такой таблицей переходов состояний^[англ.]:

Вход Состояние	0	1	ε
S₀	{}	{}	{S₁, S₃}
S₁	{S₂}	{S₁}	{}
S₂	{S₁}	{S₂}	{}
S₃	{S₃}	{S₄}	{}
S₄	{S₄}	{S₃}	{}

[math]\displaystyle{ M }[/math] можно рассматривать как объединение двух ДКА — один с состояниями [math]\displaystyle{ \{S_1, S_2\} }[/math], а другой с состояниями [math]\displaystyle{ \{S_3, S_4\} }[/math]. Язык [math]\displaystyle{ M }[/math] можно описать как регулярный язык, заданный регулярным выражением (1*(01*01*)*) ∪ (0*(10*10*)*). Мы определяем [math]\displaystyle{ M }[/math] с помощью ε-переходов, но [math]\displaystyle{ M }[/math] можно определить и без них.

Эквивалентность НКА

Чтобы показать, что НКА-ε эквивалентен НКА, сначала обратим внимание на то, что НКА является частным случаем НКА-ε, остаётся показать, что для любого НКА-ε существует эквивалентный НКА.

Пусть [math]\displaystyle{ A = (Q, \Sigma, \Delta, q_0, F) }[/math] будет НКА-ε. НКА [math]\displaystyle{ A' = (Q, \Sigma, \Delta', E(q_0), F) }[/math] эквивалентен [math]\displaystyle{ A }[/math], где для любого [math]\displaystyle{ a \in \Sigma }[/math] и [math]\displaystyle{ q \in Q }[/math] [math]\displaystyle{ \Delta'(q,a) = E(\Delta(q,a)) }[/math].

Тогда НКА-ε эквивалентен НКА. Поскольку НКА эквивалентен ДКА, НКА-ε также эквивалентен ДКА.

Свойства замкнутости

Составной НКА, принимающий объединение языков некоторых заданных НКА N(s) и N(t). Для входной строки w в объединённом языке составной автомат следует ε-переходу из q в начальное состояние (левый цветной круг) соответствующего подавтомата — N(s) или N(t) — откуда, следуя входному символу из w, можно попасть в конечное состояние (правый цветной кружок). Из этого состояния в состояние f можно попасть другим ε-переходом. Вследствие ε-переходов составной НКА вполне недетерминированный, даже если оба автомата N(s) и N(t) были ДКА. В другую сторону, построение ДКА для объединения языков (даже для двух ДКА) много более трудный процесс

Говорят, что НКА замкнут относительно (бинарной/унарной) операции. Если НКА распознаёт языки, которые получаются путём применения этой операции к распознаваемым автоматом НКА языкам. НКА замкнуты относительно следующих операций.

Объединение (см. рисунок)
Пересечение
Конкатенация
Дополнение
Замыкание Клини

Поскольку НКА эквивалентны недетерминированным конечным автоматам с ε-переходами (НКА-ε), замыкания выше доказываются с помощью свойств замыкания НКА-ε. Из свойств замыкания выше вытекает, что НКА распознают только регулярные языки.

НКА могут быть построены из любого регулярного выражения с помощью алгоритма Томпсона^[англ.].

Свойства

Машина начинает с определённого начального состояния и читает строку символов, состоящую из букв её алфавита. Автомат использует функцию переходов Δ, чтобы определить следующее состояние по текущему состоянию и только что прочитанному символу или пустой строке. Однако «следующее состояние НКА зависит не только от текущего входного символа, но и от произвольного числа последующих входных событий. Пока эти последующие события происходят, невозможно определить, в каком состоянии машина находится»^[13]. Если автомат после последнего прочитанного символа находится в конечном состоянии, говорят, что НКА принимает строку, в противном случае говорят, что он строку отвергает.

Множество всех строк, принимаемых НКА, является языком, который принимает НКА. Этот язык является регулярным языком.

Для любого НКА можно найти детерминированный конечный автомат (ДКА), который принимает тот же самый язык. Поэтому есть возможность преобразовать существующий НКА в ДКА с целью реализации (возможно) более простой машины. Такое преобразование осуществляется с помощью конструкцией подмножеств^[англ.], которое может вести к экспоненциальному увеличению числа необходимых состояний. Для формального доказательства конструкции подмножеств см. статью «Конструкция подмножеств^[англ.]».

Реализация

НКА можно моделировать одним из следующих способов:

Преобразование в эквивалентный ДКА. В некоторых случаях это может привести к взрывному росту числа состояний^[14].
Поддержание множества всех состояний, в которых НКА может оказаться после чтения слова. При обработке входного символа необходимо объединить результаты функции переходов, применённой к текущему множеству состояний, чтобы получить следующее множество. Если разрешены ε-переходы, нужно также включить все состояния, достижимые по таким переходам (ε-замыкание). Каждый шаг требует не более [math]\displaystyle{ s^2 }[/math] вычислений, где s — число состояний НКА. Автомат принимает строку если и только если при обработке последнего входного символа, одно из текущих состояний является конечным. Строка длины n может быть обработана за время O(ns²)^[15] с использованием O(s) памяти.

Приложения НКА

НКА и ДКА эквивалентны в том смысле, что если язык распознаётся НКА автоматом, он распознаётся и ДКА. Верно и обратное. Установление такой эквивалентности важно и полезно. Важно, поскольку НКА могут использоваться для уменьшения сложности математической работы, которая нужна для установления важных свойств в теории алгоритмов. Например, много легче доказать замкнутость регулярных языков с помощью НКА, чем с помощью ДКА. Полезно, потому что построение НКА для распознавания этого языка иногда много важнее построения ДКА для этого языка.

См. также

Примечания

↑ Martin, 2010, с. 108.
↑ Rabin, Scott, 1959, с. 114–125.
↑ Последовательность выборов может привести в «тупик», в котором ни один из переходов неприменим для текущего входного символа и это случай считается неудачей (строка отвергается).
↑ Hopcroft, Ullman, 1979, с. 19.
↑ Aho, Hopcroft, Ullman, 1974, с. 319.
↑ Hopcroft, Ullman, 1979, с. 19—20.
↑ Sipser, 1997, с. 48.
↑ Hopcroft, Motwani, Ullman, 2001, с. 56.
↑ Aho, Hopcroft, Ullman, 1974, с. 320.
↑ Sipser, 1997, с. 54.
↑ Hopcroft, Ullman, 1979, с. 21.
↑ Hopcroft, Motwani, Ullman, 2001, с. 59.
↑ Finite-State Machine FOLDOC Free Online Dictionary of Computing (неопр.). Дата обращения: 11 февраля 2020. Архивировано 4 апреля 2015 года.
↑ Chris Calabro. NFA to DFA blow up. 2005-02-27 (неопр.). Дата обращения: 11 февраля 2020. Архивировано 7 февраля 2013 года.
↑ Hopcroft, Motwani, Ullman, 2001, с. 153.

Литература

Alfred V. Aho, John E. Hopcroft, Jeffrey D. Ullman. The Design and Analysis of Computer Algorithms. — Reading/MA: Addison-Wesley, 1974. — ISBN 0-201-00029-6.
- Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. — Москва: «Мир», 1979.
John E. Hopcroft, Jeffrey D. Ullman. Introduction to Automata Theory, Languages, and Computation. — Reading/MA: Addison-Wesley, 1979. — ISBN 0-201-02988-X.
- John Hopcroft, Rajeev Motwani, Jeffrey Ullman. Introduction to Automata Theory, Languages, and Computation. — 2. — Addison Wesley, 2001. — ISBN 0-201-44124-1.
- Джон Хопкрофт, Раджив Мотвани, Джеффри Ульман. Введение в теорию автоматов, языков и вычислений = Introduction to Automata Theory, Languages, and Computation. — М.: «Вильямс», 2002. — 528 с. — ISBN 0-201-44124-1.
Michael Sipser. Introduction to the Theory of Computation. — Boston/MA: PWS Publishing Co., 1997. — ISBN 0-534-94728-X.
John Martin. Introduction to Languages and the Theory of Computation. — McGraw Hill, 2010. — ISBN 978-0071289429.
Rabin M. O., Scott D. Finite Automata and Their Decision Problems // IBM Journal of Research and Development. — 1959. — Апрель (т. 3, вып. 2). — doi:10.1147/rd.32.0114.
Allan C., Avgustinov P., Christensen A. S., Hendren L., Kuzins S., Lhoták O., de Moor O., Sereni D., Sittampalam G., Tibble J. Adding trace matching with free variables to AspectJ // In Proceedings of the 20th Annual ACM SIGPLAN Conference on Object Oriented Programming, Systems, Languages, and Applications. — San Diego, CA, USA: OOPSLA '05. ACM, New York, NY, 2005. — С. 345—364. Архивная копия от 18 сентября 2009 на Wayback Machine

[_907782feb9fd6758-1] Martin, 2010, с. 108.

[_e052c5114c39c59f-2] Rabin, Scott, 1959, с. 114–125.

[DE-3] Последовательность выборов может привести в «тупик», в котором ни один из переходов неприменим для текущего входного символа и это случай считается неудачей (строка отвергается).

[_1cd21305018e734d-4] Hopcroft, Ullman, 1979, с. 19.

[_e6d3b1f8de788aa7-5] Aho, Hopcroft, Ullman, 1974, с. 319.

[_13834134a7ea080b-6] Hopcroft, Ullman, 1979, с. 19—20.

[_f3ed8c06ff8b2415-7] Sipser, 1997, с. 48.

[_d9520243eab99cfa-8] Hopcroft, Motwani, Ullman, 2001, с. 56.

[_e6d3b0f8de7888db-9] Aho, Hopcroft, Ullman, 1974, с. 320.

[_f3ed8b06ff8b224e-10] Sipser, 1997, с. 54.

[_1cd21605018e78bc-11] Hopcroft, Ullman, 1979, с. 21.

[_d9520243eab99cf5-12] Hopcroft, Motwani, Ullman, 2001, с. 59.

[FD-13] Finite-State Machine FOLDOC Free Online Dictionary of Computing (неопр.). Дата обращения: 11 февраля 2020. Архивировано 4 апреля 2015 года.

[14] Chris Calabro. NFA to DFA blow up. 2005-02-27 (неопр.). Дата обращения: 11 февраля 2020. Архивировано 7 февраля 2013 года.

[_ffe94267d95a3c3c-15] Hopcroft, Motwani, Ullman, 2001, с. 153.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

Формальные языки и формальные грамматики
Общие понятия	Иерархия Хомского Алфавит Слово
Тип 0	Неограниченная грамматика Машина Тьюринга Перечислимый язык Разрешимый язык
Тип 1	Контекстно-зависимая грамматика Контекстно-зависимый язык^[англ.] Линейно ограниченный автомат^[англ.]
Тип 2	Контекстно-свободная грамматика Неоднозначная грамматика Контекстно-свободный язык Автомат с магазинной памятью (детерминированный^[англ.]) Лемма о разрастании Лемма Огдена Теорема Кука
Тип 3	Регулярная грамматика Регулярный язык Регулярное выражение Конечный автомат (детерминированный, недетерминированный) Минимизация ДКА Детерминизация НКА^[англ.] Теорема Майхилла — Нероуда
Синтаксический анализ	LL-анализатор LR-анализатор Метод рекурсивного спуска Алгоритм Кока — Янгера — Касами